5.1. Автоматизация дедуктивных рассуждений. Поиск доказательств теорем методом резолюций.

Многие интересные и практически важные задачи могут быть сформулированы как задачи доказательства теорем в подходящем логическом исчислении.

Перечислим некоторые из таких задач.

1. Дедуктивные вопросно – ответные системы. В вопросно – ответных системах факты могут быть представлены логическими формулами. Тогда для ответа на некоторый вопрос следует доказать, что формула, соответствующая ответу, логически выводима из фактов.

2. Задача анализа программ. В задаче анализа программ выполнение программы можно описать формулой А, а условие завершения работы программы – формулой В. Тогда проверка того, что программа завершит работу эквивалентна доказательству того, что формула В следует из формулы А

3. Задача синтеза программ. Если условие и результат задачи можно представить в виде логических формул, то решение задачи можно рассматривать как логический вывод результата из формул условия.

Программа же решения задачи извлекается в этом случае из вывода.

4. Изоморфизм графов. Часто требуется выяснить, изоморфен ли граф подграфу другого графа. Задача может быть сформулирована как задача выводимости формулы, представляющий один граф из формулы, представляющей другой граф.

Поскольку все перечисленные задачи относятся к трудным вычислительным задачам, то через некоторое время после появления вычислительных машин, а именно, во второй половине 60-х годов наблюдался резкий всплеск интереса к машинному автоматическому поиску доказательств теорем.

На самом деле поиск универсальной разрешающей процедуры для проверки общезначимости формул был начат еще Лейбницем в 17 веке. В дальнейшем эти попытки возобновили Пеано (на рубеже 20 века) и Гильберт со своими учениками в 20-х годах 20 века.

Эти попытки продолжались до тех пор, пока Черч и Тьюринг в 1936 году не доказали, что никакой общей разрешающей процедуры для проверки общезначимости формул не существует, иначе говоря, не существует универсального алгоритма, проверяющего общезначимость формул в логике первого порядка.

Это не означает, однако, что общезначимость формулы установить невозможно. Существуют алгоритмы, которые могут установить, что формула общезначима, если она на самом деле общезначима. Если же она не является общезначимой, то эти алгоритмы вообще говоря, никогда не закончат свою работу. Это лучшее, что можно ожидать от универсальных алгоритмов поиска доказательства.

Теоретические основы соответствующих компьютерных методов были заложены в 1930 г. Эрбраном. Первые же практически важные шаги на пути создания программ автоматического доказательства теорем были сделаны после основополагающих работ С.Ю.Маслова [17] об обратном методе установления выводимости в классическом исчислении предикатов и Дж.А.Робинсона [18] о методе резолюций , выполненных ими независимо в 1964 и 1965 годах, соответственно.

Скулемовская стандартная форма.

При поиске доказательства методом резолюций используются так называемые Скулемовские стандартные формы формул исчисления предикатов первого порядка.

При приведении формулы к Скулемовской стандартной форме используются следующие соображения:

1. Формула логики первого порядка может быть приведена к предваренной нормальной форме, в которой все кванторы содержатся в префиксе (т.е. ни одному квантору не предшествует предикатный символ).

2. Матрица (т.е., часть формулы, следующая за префиксом и не содержащая кванторов) может быть сведена к коньюктивной нормальной форме.

3. В формуле можно элиминировать кванторы существования с помощью скулемовских функций.

Рассмотрим вначале метод приведения формулы к предваренной нормальной форме [19]. Для этого рассмотрим основные законы эквивалентности в логике первого порядка. Здесь мы полагаем, что х и y являются свободными переменными в А и В, соответственно:

1. -

2. 

3. 

4. 

5. 

6. .

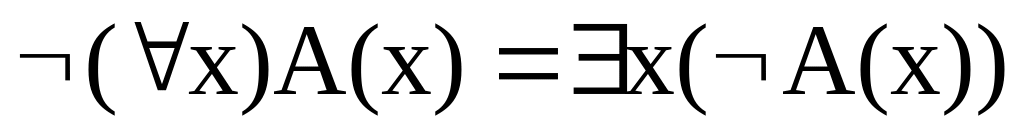
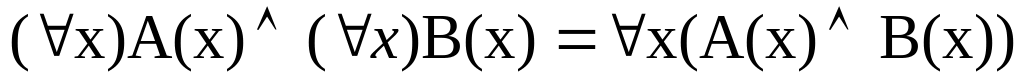
Имеется и ряд других эквивалентностей, которые будут использоваться по мере необходимости.

Здесь уместно заметить, что квантор всеобщности  и квантор существования  нельзя проносить через дизъюнкцию и конъюнкцию, соответственно, т.е.

_{В таких случаях, надо вспоминать, что связанная переменная – лишь место для подстановки какой угодно переменной и, следовательно, каждую связанную переменную можно переименовать. Например, формулу}

можно преобразовать в формулу _{где z не встречается в А(x). Тогда}

Аналогичным образом преобразуется и формула

Далее, формулу следует привести к следующему виду:

(Q₁х₁).. (Q_nх_n)(M),

где каждое Q_iх_i (i=1,2,…,n) есть или (x_i ) или (x_i),а М есть формула, не содержащая кванторов. Такой вид и будет называться предваренной нормальной формой.

Тогда (Q₁х₁).. (Q_nх_n) называют префиксом, а М- матрицей формулы

Опишем теперь кратко алгоритм приведения формул к предваренной нормальной форме [17]:

1. Если в формуле присутствуют логические связки

• и , то применим к ней законы

_{для исключения этих связок.}

_{2.Если перед формулой имеется знак отрицания, то используем законы}

_{(F) = F}

и законы

_,

_{для того чтобы пронести знак отрицания внутрь формулы.}

_{3.Если необходимо, переименовываем связанные переменные.}

4. Выносим кванторы в начало формулы, для чего используем законы

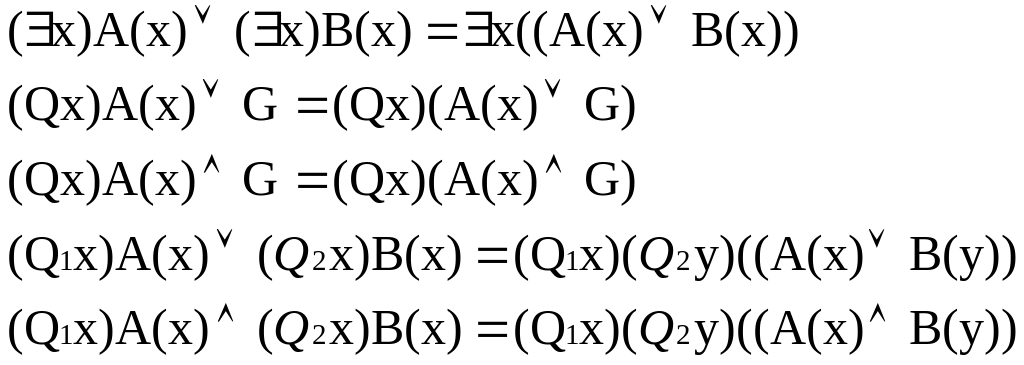
_{Далее следует М - матрицу формулы привести к конъюнктивной нормальной форме.}

_{Для этого введем следующие определения:}

_{Определение 5.1. Литерой будем называть атомарную формулу или ее отрицание.}

_{Определение 5.2. Формула F находится в конъюнктивной нормальной форме тогда и только тогда, когда F имеет вид}

n 1, а каждая F₁ ,F₂,…,F _{n есть дизъюнкция литер.}

_{Приведем схематическое описание процедуры преобразования к конъюнктивной нормальной форме (впрочем, следует заметить, что эта же схема годится и для дизъюнктивной нормальной формы):}

_{1. Элиминируем логические связки  и  применяя эквивалентности}

_{2.Проносим знак отрицания к атомам, используя, (возможно, несколько раз) законы}.

_{(F) = F}

3.Используем (возможно, несколько раз) законы

для получения нормальной формы.

После выполнения соответствующих процедур, для приведения формулы к Скулемовской нормальной форме осталось элиминировать кванторы существования. Это выполняется следующим образом:

пусть формула имеет вид (Q₁х₁).. (Q_nх_n)(M), где М есть конъюнктивная нормальная форма и пусть некоторое Q_i есть квантор существования в префиксе (Q₁х₁).. (Q_nх_n)(M).

Если в указанном префиксе левее Q_i нет никакого квантора всеобщности, выбирается новая константа c, отличная от всех иных констант, входящих в М и все x_i в М заменяются на с. Если же левее Q_i встречаются кванторы всеобщности Q_,…,Q_ выбирается новый m-местный функциональный символ f, отличный от всех иных функциональных символов в М, то все x_i в М заменяются на f(x_,…,x_) и (Q_ix_i)вычеркивается из префикса. Затем это процесс применняется ко всем кванторам существования в префиксе. Последняя из полученных таким образом формул и есть скулемовская нормальная форма. Константы и функции, используемые для замены переменных, связанных кванторами существования, называются скулемовскими функциями.

Введем понятие дизъюнкта:

Определение 5.3.Дизъюнкция литер называется дизъюнктом.

Далее, там где это будет удобно, будем рассматривать как синоним дизъюнкта множество литер.