Алгоритм strips

Алгоритм STRIPS приведен в табл.1

STRIPS вход: R, s, G выход: plan 1 S=S0 2 пока G не выполнимо в s делать 2.1. выбрать компоненту g из G 2.2. выбрать правило RR такое, что gA(R) 2.3. STRIPS (R, s, C(R)) 2.4. применить R к s 2.5. добавить R в plan 3 вернуть plan

Табл.1. Алгоритм STRIPS

На вход алгоритма STRIPS подаётся множество правил R, начальное состояние s₀, цель G.

Будем полагать, что в множестве R все правила полностью конкретизированы.

Вначале в стек целей помещается главная цель G.

Если цель не является простой, т.е. содержит конъюнкцию литералов, то система STRIPS добавляет в стек в некотором порядке каждый из литералов составной цели (п.1.1). Когда верхняя цель стека является однолитеральной, система ищет действие (п.1.2), которое содержит в списке добавлений литерал, сопоставимый с этой целью. Если такое действие не применимо к текущему состоянию, тогда его предусловие помещается в стек целей, иначе действие применяется к текущему состоянию (п.1.5.) и помещается в план (plan). Если верхняя цель в стеке соответствует текущему состоянию, то она удаляется из стека. Алгоритм STRIPS завершается, когда стек пуст.

Неполнота алгоритма strips.

Существуют задачи, для которых STRIPS либо не может построить план, либо находит не минимальный план.

Причина этого кроется в том, что STRIPS удовлетворяет каждую компоненту составной цели по отдельности, без учёта их взаимосвязи. Особенность предметной области, где цели взаимосвязаны (взаимодействуют) получила название взаимосвязи целей.

Примечание. Впервые некорректность STRIPS'а в этом случае была вскрыта в 1973 году Аленом Брауном из Массачусетского Технологического института. Браун попытался решить задачу, рассматриваемую в этом разделе на планировщике HACKER. HACKER был создан Джеральдом Суссманом на основе планировщика STRIPS, поэтому задача получила название аномалия Суссмана (Sussman Anomaly) [58] .

Рассмотрим аномалию Суссмана

Дано:

Объекты:

3 кубика – A, B, C.

Состояние описывается предикатами:

ontable (x) – кубик x на столе,

clear (x) – над кубиком x пусто,

handempty – рука агента пуста,

holding (x) – рука агента держит кубик x,

on (x,y) – кубик x находится на кубике y.

x, y –переменные.

Правила:

R1: pickup (x) – поднять кубик со стола

C (R1): ontable (x) & clear (x) handempty

A (R1): holding (x)

D (R1): ontable (x), clear (x), handempty

R2: putdown (x) – опустить кубик на стол

C (R2): holding (x)

A (R2): ontable (x), clear (x), handempty

D (R2): holding (x)

R3: stack (x,y) – положить кубик на другой кубик

C(R3): holding (x) & clear (y)

A(R3): handempty, on (x,y), clear (x)

D(R3): holding (x), clear (y)

R4: unstack (x,y) – снять кубик с другого кубика

C(R4): handempty & on(x,y) & clear (x)

A(R4): holding (x), clear (y)

D(R4): handempty, on(x,y), clear (x)

Начальное состояние s₀ и цель G изображены на рис.1.

Таким образом, цель G= {On (A,B) & On (B,C)}.

Рис.1. Аномалия Суссмана

Поскольку цель G является составной, то STRIPS расщепляет её на отдельные компоненты – On (A,B) и On (B,C), которые помещаются в стек и удовлетворяются по очереди.

Положим, что On (A,B) наверху стека, тогда планировщик находит следующую последовательность правил для удовлетворения On (A,B): UNSTACK(C,A), PUTDOWN(C), PICKUP(A), STACK (A,B). Применяет найденную последовательность к состоянию s₀. Получается ситуация, изображённая на рис.2, в которой On (A,B) выполнима. Цель On (A,B) удаляется из стека целей.

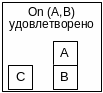
Рис. 2. Удовлетворение первой цели

Далее, из ситуации на рис.2 , удовлетворяется следующая цель в стеке – On (B,C). В результате имеем: UNSTACK(C,A), PUTDOWN(C), PICKUP(A), STACK (A,B), UNSTACK(A,B), PUTDOWN(A), PICKUP(B), STACK (B,C). Применяем последовательность подчёркнутых правил. Получаем ситуацию на рис.3. Цель On (B,C) удовлетворена и удаляется из стека. Однако цель On(A,B), удовлетворённая на предыдущем этапе, перестаёт быть выполнимой.

Рис. 3. Удовлетворение второй цели

Поэтому, далее планировщик пытается из ситуации на рис.3 удовлетворить On (A,B). Это приводит к добавлению ещё двух правил к имеющейся последовательности.

В результате получаем план: UNSTACK(C,A), PUTDOWN(C), PICKUP(A), STACK (A,B), UNSTACK(A,B), PUTDOWN(A), PICKUP(B), STACK (B,C), PICKUP(A), STACK (A,B). Подчёркнутые правила применяются. Цель On (A,B) & On (B,C) достигается. План построен.

Однако существует другой план, содержащий меньше действий:

UNSTACK(C,A), PUTDOWN(C), PICKUP(B), STACK (B,C), PICKUP(A), STACK(A,B).

Список литературы

1. C.Клини. Математическая логика.М.:МИР,1973

2. Г.Кейслер, Ч.Ч.Чен. Теория моделей. М.: Мир, 1977.

3. Мальцев А.И. Алгебраические системы. М.: Наука, 1970

4. Fikes R.E., Nilsson N.J. STRIPS: a new approach to application of theorem proving to problem

solving. Artificial Intelligence 1971, 2.

5. Нилсон Н.Принципы искусственного интеллекта. М. МИР, 1977

6. Лорьер Ж.-Л. Системы искусственного интеллекта.М.:МИР, 1991

7. Quillian M.R. Semantic memory // Semantic Information Processing, с. 227-268, MIT Press, 1968

8. Р.Ковальски, Логика в решении проблем. М.: «НАУКА», 1990

9. В.Н.Вагин. Дедукция и обобщение в системах принятия решений.

М.: НАУКА, 1988

10. Г.С.Осипов. Приобретение знаний интеллектуальными системами. М.Наука. ФИЗМАТЛИТ, 1997.

11. Жилякова Л.Ю. Об одном классе отношений в неоднородных семантических сетях.// Изв. ТРТУ №2, Таганрог, 2000, стр. 70-73.

12. Клещёв А.С. Семантические порождающие модели. Общая точка зрения на фреймы и продукции в экспертных системах. Препринт. Владивосток: ИАПУ ДВНЦ РАН, 1986,

39 стр.

6. 13. Donini, Francesco M., Maurizio Lenzerini, Daniele Nardi, Werner Nutt. The Complexity of Concept Language. // In Proc. of the 2^nd Int. Conf. On the Principles of Knowledge Representation and Reasoning (KR-91), 1991.

7. 14. Dorofeyeva A. Analysis of Semantic Networks By Means of Description Logics// In Proceedings of the 1999 International Workshop on Description Logics(DL'99) Linkцping, Sweden July 30 - August 1, 1999. pp.167 – 168.

8. 15. Шушакова А.Г. Решение задач представления и обработки знаний средствами дескриптивной логики. // Программные продукты и системы №3, 2002 – М: НТП «Фактор» – с. 14 – 19.

9. 16.Donini F.M., Lenzerini M., Nardi D., Nutt W., Reasoning in Description Logics // In Procedings of the Second International Conference on Principles of Knowledge Representation and Reasoning. (KR-91), pp. – 151 – 162, 1991.

10. 17.Donini F.M., Lenzerini M., Nardi D., Nutt W., The complexity of concept languages // Inform.and Comp. 134, 1997. pp: 1-58.

12. 18. Kurtonona N., Rijke M., Expressivenes of concept espressions in first-order description logics // Artificial Intelligence, v.107, 1999.

13. 19. F.Baader, PHanschke. A Scheme for Integrating Concrete Domains into Concept Languages.

14. Proc. IJCAI-91, Sydney, Australia, 1991, p 452-457.

15. 20. Lutz C., Reasoning with Concrete Domains // Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence (IJCAI'99), 31 july – 6 august, 1999, Stockholm, Sweden.

17. С.Ю.Маслов. Обратный метод установления выводимости в классическом исчислении предикатов // Доклады АН СССР, - 1964, т. 159, № 1, стр. 17-20

18. Robinson J. A. Machine Oriented Logic Based on the Resolution Principle. J. ACM, 12 (January 1965), pp.23 – 41.

19. Ч.Чень, Р.Ли.Математическая логика и автоматическое доказательство теорем.

М.:»Наука», 1983

20. В.К.Финн. Интеллектуальные системы и общество. М.: УРСС, 2006

21. В.Н.Вагин, Е.Ю.Головина, А.А.Загорянская, М.В. Фомина. Достоверный и правдоподобный вывод в интеллектуальных системах. М.: Физматлит, 2004

22. Финн В.К. Правдоподобные рассуждения в ителлектуальных системах тиа ДСМ // Итоги науки и техники. М., 1991. Т. 15, стр. 54-101.

23. Аншаков О.М. Об одной интерпретации ДСМ-метода автоматического порождения гипотез. // НТИ*, №1, 1999.

 

24. Prakken, H. & Vreeswijk, G.A.W. (2002). Logics for defeasible argumentation. In D.M. Gabbay & F. Guenthner (Eds.), Handbook of Philosophical Logic, 2nd edition, Vol 4 (pp. 219-318). Dordrecht/Boston/London: Kluwer Academic Publishers.

25. А.Б.Беляев, М.Н.Годовников, С.А.Голубев, Е.П.Куршев, Г.С. Осипов, Л.И.Сазонова. Технология создания распределённых интеллектуальных систем. Учебное пособие. Университет г. Переславля, Переславль-Залесский, 1997.

26. Gordon A.D., Classification. London: Chapman & Hall, 1999.

27. Эфрон Б. Нетрадиционные методы многомерноо статистического аализа. М.: Финансы и статистика, 1988.

28. Назаренко Г.И., Осипов Г.С. Основы теории медицинских технологических процессов. Ч.2. Иследование медицинских технологических процессов на основе интеллектуального анализа даных. М.: Наука, Физматлит, 2006.

29. Аркадьев А.Г., Браверман Э.М. Обучение машины распознаванию образов. М.: Наука, 1964.

30. Lenz, Mario; Bartsch-Sporl, Brigitte; Burkhard, Hans-Dieter; Wess, Stefan (ed).

Case-Based Reasoning Technology: From Foundations to Applications. Lecture Notes in Artificial Intelligence. Springer, 1998.

31. Kumar V. Algorithms for constraint-satisfaction problems: A survey. // AI Magazine, 13(1):32--44, 1992. http://citeseer.nj.nec.com/kumar92algorithms.html

32. Kambhampati S., Nigenda R., Nguyen X. AltAlt: Combining the advantages of Graphplan and Heuristic State Search. // ASU Technical Report

33. Maler O., Manna Z., Pnueli A. From Timed to Hybrid systems // Real-Time: Theory in Practice, LNCS, Vol.600, с.447-484, Springer-Verlag, 1992

34. McCarthy J. Formalisation of STRIPS in situation calculus // Technical report formal reasoning Group, Dep. of Computer Science, Stanford University, 1985

35. Williams B., Nayak P. A Reactive Planner for a Model-Based Execution // Proceedings of the Fifteenth International Joint Conference on Artificial Intelligence (IJCAI-15). – Menlo Park, California, 1997. – c.1178-1185

36. Long D., Fox M. Efficient Implementation of the Plan Graph in STAN, V.10, p. 87-115, 1999

37. Raphael B. The frame problem in problem solving systems // Artificial Intelligence and Heuristic Programming. –1971, c.159-169. Edinburgh Univ. Press, Edinburgh, Scotland

38. McDermott, D. A Heuristic Estimator for Means-Ends Analysis in Planning // In Proceedings of the Third International Conference on AI Planning Systems. – 1996. –c.142–149. Menlo Park, Calif.: AAAI Press

39. Sussman G. A Computational Model of Skill Acquisition. // PhD thesis, MIT, Cambridge, Massachusetts, August 1973

40. Chapman D. Planning for Conjunctive Goals // Artificial Intelligence. - 1987. – №32(3). – с.333–377

41. Tate A. Generating Project Networks // Proceedings of the Fifth International Joint Conference on Artificial Intelligence. – Menlo Park, California. – 1977. – с.888–893

42. McAllester D., Rosenblit D. Systematic nonlinear planning // Proceedings of AAAI-91, Anaheim, Ca, 1991

43. Sacerdoti E.D. Planning in a hierarchy of abstraction spaces // Artificial Intelligence. – 1974. – №5. – С.115-135

44. Sacerdoti E.D. The nonlinear nature of plans // Proceedings of the Fourth International Joint Conference on Artificial Intelligence (IJCAI-75). – Tbilisi, Georgia. – 1975. – c.206-214

45. Tate A., Currie K. O-Plan: The Open planning architecture // Artificial Intelligence. – 1991. – № 52. – с.49-86

46. Wilkins D. Can AI planners solve practical problems? // Computational Intelligence. – 1990. – Том 6. – №4. – с.232-246

47. Blum A., Furst M. Fast planning through planning graph analysis // Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI – 95). – Montreal, Canada. – 1995. – с.1636 – 1642

48. Kautz H., Selman B. Planning as Satisfiability // Proceedings of the Tenth European Conference on Artificial Intelligence ({ECAI}'92)", с.359-363, 1992.

49. Koehler J., Nebel B., Hoffmann J., Dimopoulos Y. Extending Planning Graphs to an ADL Subset, ECP-97, pages 273-285, Springer LNAI 1348

50. Stoerr H. BDDPlan // http://www.ki.inf.tu-dresden.de/~stoerr/bddplan.html

51. Bonet B., Geffner H. Planning as heuristic search. // Artificial Intelligence. –2001. http://citeseer.nj.nec.com/bonet01planning.html

52. Hoffmann J., Nebel B. The FF planning system: Fast plan generation through heuristic search // Journal of Artificial Intelligence Research, 2001

53. Kambhampati S., Nigenda R., Nguyen X. AltAlt: Combining the advantages of Graphplan and Heuristic State Search. // ASU Technical Report

54. Refanidis I., Vlahavas I. "The GRT Planner: Backward Heuristic Construction in Forward State-Space Planning", Journal of Artificial Intelligence Research, 15 (2001), с. 115-161

55. Green C.C. Theorem proving by resolution as a basis for question answering systems. In Bernard Meltzer and Donald Michie, editors // Machine Intelligence, Edinburgh University Press, Edinburgh, Scotland, 1969, 4

56. Fikes R.E., Nilsson N.J. STRIPS: a new approach to application of theorem proving to problem solving // Artificial Intelligence 1971, 2

57. Newell A., Simon H. GPS, a program that simulates human thought // Computers and Thought, eds: E.A. Feigenbaum and J. Feldman, McGraw Hill, NY, 1963

58. Sussman G. A Computational Model of Skill Acquisition. // PhD thesis, MIT, Cambridge, Massachusetts, August 1973

59. Erol K., Nau D., Subrahmanian V. Complexity, Decidability and Undecidability Results for Domain-Independent Planning. A Detailed Analysis / Технический отчёт Университета Мэрилэнд №CS-TR-2797

60. Pednault E. ADL and the state-transition model of action // Journal of Logic and Computation. – 1994. – № 4(5). – с. 467-512

61. Planning, scheduling and constraint satisfaction: from theory to practice. IOS Press, 2005

62.Тарханов Т.С. Семейство алгоритмов автоматического синтеза планов целенаправленного поведения в доменах планирования с обратимостью

// Препринт ИПС РАН.—2004

63.Blum A., Furst M. Fast planning through planning graph analysis // Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI – 95). – Montreal, Canada. – 1995. – с.1636 – 1642

64. Трофимов И. В. Использование фокусировки при решении задач планирования. Труды XI Национальной конференции по искусственому интеллекту. Дубна, 2008.

65 S. Hanks, D.S. Weld. A Domain-Independent Algorithm for Plan Adaptation. Journal of Artificial Intelligence Research, vol. 2, pp. 319-360, 1995

66. Laurie H. Ihrig, Subbarao Kambhampati Derivational Replay for Partial-Order Planning. In Proceedings AAAI-94, 1994.

67. D.B. Leake, A. Kinley, D.C. Wilson. A Case Study of Case-Based CBR. In proc. International Conference on Case-Based Reasoning, pp. 371-382, 1997.

68. R.Bergmann, W. Wilke. PARIS: Flexible Plan Adaptation by Abstraction and Refinement. In ECAI'96 Workshop "Adaptation in CBR", Budapest, 1996.

69. R. Alterman. Issues In Adaptive Planning. Report No. UCB/CSD 87/304, 1986.

70. K. Sycara. Using Case-Based Reasoning for Plan Adaptation and Repair. In Proc. of the DARPA Case-Based Reasoning Workshop, 1988.

71. K.J. Hammond. Explaining and Repairing Plans that Fail. Artificial Intelligence, 45(1-2):173-228, 1990.

72. Veloso M.M., Carbonell J.G. Towards Scaling Up Machine Learning: A Case Study with Derivational Analogy in PRODIGY. In Machine Learning Methods for Planning, Morgan Kaufmann, ed. S. Minton, pp. 233-272, 1993.

73. С.Н.Васильев, А.К.Жерлов, Е.А.Федосов, ,Б.Е.Федунов.

Интеллектное управление динамическими системами. М.: ФИЗМАТЛИТ, 2000

74. Осипов Г.С. Динамика в системах, основанных на знаниях // Известия РАН. Теория и системы управления. ¾ №5. – 1998. – с.24-28.

75. Osipov Gennady. Dynamics in Integrated Knowledge-Based Systems. Proceedings

of the 1998 IEEE Joint Conference, Gaithersburg, MD, USA, September , 1998.

76. Gennady Osipov. Attainable Sets and Knowledge Base Architecture in Discrete Dynamic

Knowledge-based Systems. Proc. Of Workshops of the ECAI 2000 14-th European Conference

of Artificial Intelligence. Berlin. 2000, 39-43.

77. Лебедева Т.Г., Осипов Г.С. Архитектура и управляемость дискретных динамических систем, основанных на знаниях. // Известия АН. Теория и системы управления. ¾ №5. – 2000. – с.703-709.

78. Виноградов А. Н., Осипов Г.С., Жилякова Л.Ю. Динамические интеллектуальные системы.

Ч.1. Представление знаний и основные алгоритмы. Известия АН. Теория и системы управления, М: Наука, 2002, №6, 119-127

79.Виноградов А. Н., Осипов Г.С., Жилякова Л. Ю. Динамические интеллектуальные системы.

Ч.2. Моделирование целенаправленного поведения. Известия АН.

Теория и системы управления, М: Наука, 2003, №1. стр.

80. Г.С.Осипов. Динамические интеллектуальные системы. Искусственный интеллект и

принятие решений, М.: URSS, 2008, № 1.

81. Месарович М., Такахара Я. Общая теория систем. Математические основы. – М.: Мир, 1978. – 311с.

82. Р.Калман, П.Фалб, М.Арбиб. Очерки по математической теории систем.

М.: МИР, 1971.

83. Стефанюк В.Л. Поведение квазистатической оболочки в изменяющейся нечёткой среде // Труды 4-ой национальной конференции по искусственному интеллекту (КИИ-94), т.1 // Рыбинск, 1994, с.199-203.

84. Мееров М.В. Синтез структур систем автоматического регулирования высокой точности. М.:Наука, 1967.

85. Емельянов С.В., Коровин С.К. Новые типы обратной связи. Управление при неопределённости.- М.: Наука. Физматлит, 1997, 352 стр.

86. Емельянов С.В., Коровин С.К.Расширение множества типов обратных связей и их применение при построении замкнутых динамических систем//Изв.АН СССР. Техническая кибернетика. 1981 №5, С. 173-183.

87. Емельянов С.В., Коровин С.К. Новые типы обратной связи. Синтез нелинейного управления в условиях неопределённости// Юбилейный сборник трудов ОИВТиА РАН.

Т.1. 1993. С. 115-137.

88. Т.А.Гаврилова, В.Ф.Хорошевский. Базы знаний интеллектуальных систем.

С.-Петербург.: ПИТЕР, 2000

89. Boose J.H. Personal Construct Theory and the Transfer of Human Expertise. Advances in Artificial Intelligence/Ed.T.O`Shea.North-Holland: Elsevir, 1984, p. 27-33

90. J. Kelly. The Psychology Personal Constructs.- N.Y.:Norton, 1955

91. Т.А.Гаврилова, К.Р.Червинская. Извлечение и структурирование знаний для экспертных систем. М.: Радио и связь,, 1992

92. G.S.Osipov. The Method of direct Knowledge Acquisition from human experts. Proceeding of the 5th Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, Banff, Canada, November, 1990 , pp.104-116.

93. Cтепанов Ю.С. Имена, предикаты, предложения. Семиологическая грамматика. – М.: Наука, 1981, 360 стр.

94. Караулов, Ю.Н. Общая и русская идеография. – М.: Наука, 1976

95. Ю.И.Журавлев. Об алгебраическом подходе к решению задач распознавания или классификации. Проблемы кибернетики, Т.38, с. 5-68.

96. Quinlan, J, R. Induction of Decision Trees. Machine Learning 1:81-106,1986

97. Michalski, R. S. A Theory and Methodology of Inductive Learning. Artificial Inteligence, 20:111-161, 1983

98. Michalski, R.S. and Stepp, R. Learning from Observation: Conceptual Clustering. In: R.S.

Michalski, J.G. Carbonnell, and T.M.Mitchell (eds): Machine Learning: An Artificial Intelligence Approach, Morgan Kaufmann.

99. Mitchell, T.M. Machine Learning, McGraw Hill, 1996.

100. Hirsh, H. Incremental Version-Space Merging: A General Framework for Concept Learning. Kluwer Academic Publishers, 1990.

101. Winston, P.H. Learning Structural Descriptions from Examples. Technical report AI-TR-231, MIT Cambridge, MA, 1970

102. Miroslav Kubat, Ivan Bratko, Ryszard Michalsky. A Review of Machine Learning Methods. In: Machine Learning and Data Mining: Methods and Applications, John Wiley&Sons Ltd, 1996

103. Niblett, T. and Bratko, I. Learning decision Trees in noisy domains. In: Expert Systems 86: Proc. Expert Systems 86 Conf. Cambridge Univ. Press

104. Michalski, R.S. AQVAL/1-Computer Implementation of a Variable-Valued Logic System VL1 and Examples of its Application to Pattern ecognition. Proc. Of the First Int. Joint Conf. on Pattern Recognition, Washington, DS, pp.3-17, 1973.

109.Люгер Д. Ф. Искусственный интеллект: стратегии и методы решения сложных проблем. - М.: Изд. дом «Вильямс», 2003. – 864 с.

114. И.М.Кобозева. Лингвистическая семантика. М.:УРСС, 2000

115. Хомский Н. Синтаксические структуры. Пер. с англ. К. И. Бабицкого и В. А. Успенского // Новое в зарубежной лингвистике. II. М.: ИИЛ, 1962. С. 412—527.

116. Montague, Richard. Formal Philosophy: Selected Papers of Richard Montague. Edited and with an introduction by Richmond Thomason, New Haven: Yale Univ. Press. 1974

117. Филлмор Ч. Дело о падеже. // Новое в зарубежной лингвистике. Вып. X. М., 1981. С. 400-444

118.Филлмор Ч. Дело о падеже открывается вновь. // Новое в зарубежной лингвистике. Вып. X. М., 1981. С. 496-530.

119. И.А.Мельчук. Опыт теории лингвистических моделей «СМЫСЛ ↔ ТЕКСТ». М.: Наука, 1974

120. Ю.Д.Апресян. Лексическая семантика. Синонимические средства языка. Избранные труы, Т.1. М.:ЯРК, 1995.

121.Золотова, Г.А.; Онипенко, Н.К.; Сидорова, М.Ю. Коммуникативная граматика руского языка. М.: Институт русского языка им. В.В.Виноградова РАН, 2004.

122. Золотова, Г.А. Синтаксическй словарь. Репертуар элементарных единиц русского синтаксиса. М.:Наука, 1988.

123. Смирнов И.В. Метод автоматического установления значений минимальных семантико-синтаксических единиц текста. Информационные технологии и вычислительные системы. 2008, № 3, с. 30-45.

124. Г.С.Осипов, И.В.Смирнов, И.А. Тихомиров. Реляционно-ситуационный метод поиска и анализа текстов и его приложения. Искусственный интеллект и принятие решений. 2008, №2, с. 3-10.

125. http://www.aot.ru

1 Структур человеческого сознания, отражающих представление личности о действительности

79