Вариант № 5.
Р ешить систему уравнений. а) по формулам Крамера; б) методом Гаусса; в) методом обратной матрицы
2x – y – z = 4,
3x + 4y – 2z = 11,
3x – 2y + 4z = 11.
Даны координаты вершин пирамиды А1А2А3А4 : А1(10;6;6), А2(-2;8;2), А3(6;8;9), А4(7;10;3).
Найти: 1)длину вектора А1А2;
2)угол между векторами А1А2 и А1А4;
3)площадь грани А1А2А3;
4)объем пирамиды;
5)уравнение прямой А1А2.
Даны вершины А(-9;2), В(3;-3), С(6;1) треугольника АВС. Требуется найти:
а) длину стороны АВ; б) уравнение стороны АВ;
в) уравнение медианы ВЕ, проведенной из вершины В;
г) уравнение высоты CD, проведенной из вершины С;
д) длину h высоты CD; е) площадь треугольника АВС. Сделать чертеж.
Составить уравнение линии, расстояния каждой точки которой от точки А(2; 0) и от прямой 2x + 5 = 0 относятся как 4:5.
Линия задана уравнением r = 1/(2 + 2cos) в полярной системе координат. Требуется: построить линию по точкам, начиная от =0 до =2 и придавая значения через промежуток /8; найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;по полученному уравнению определить вид линии.
Дано комплексное число
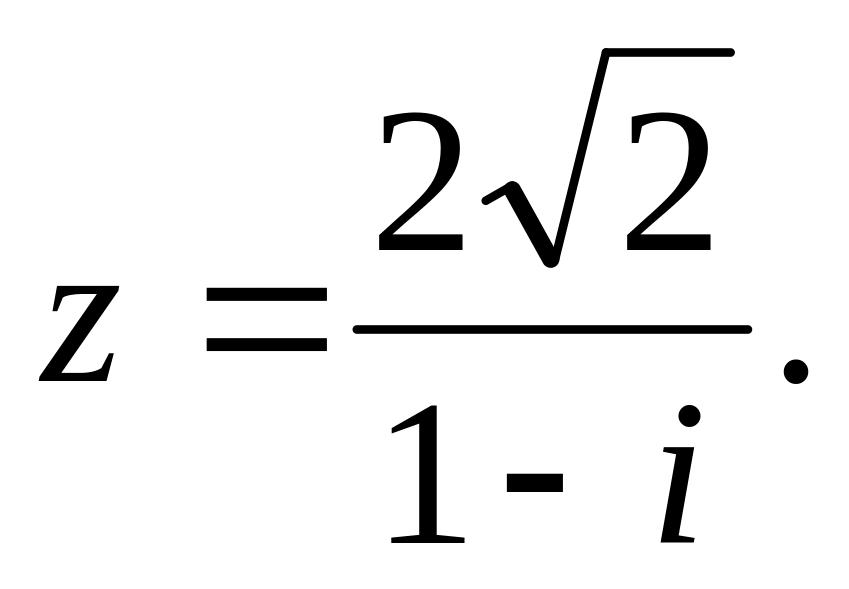Требуется:
а) записать число z в алгебраической и тригонометрической формах;
б) найти все корни уравнения a3 + z = 0.
Найти пределы функций, не пользуясь правилом Лопиталя.
1)
2)
3)
4)
Найти производные следующих функций.
1)
2)
3)
4)
5)
Найти 1)
2)
Найти приближенное значение cos32° с помощью дифференциала соответствующей функции.
Найти наибольшее и наименьшее значения функции y = x – sin x на отрезке
.Исследовать методами дифференциального исчисления функцию
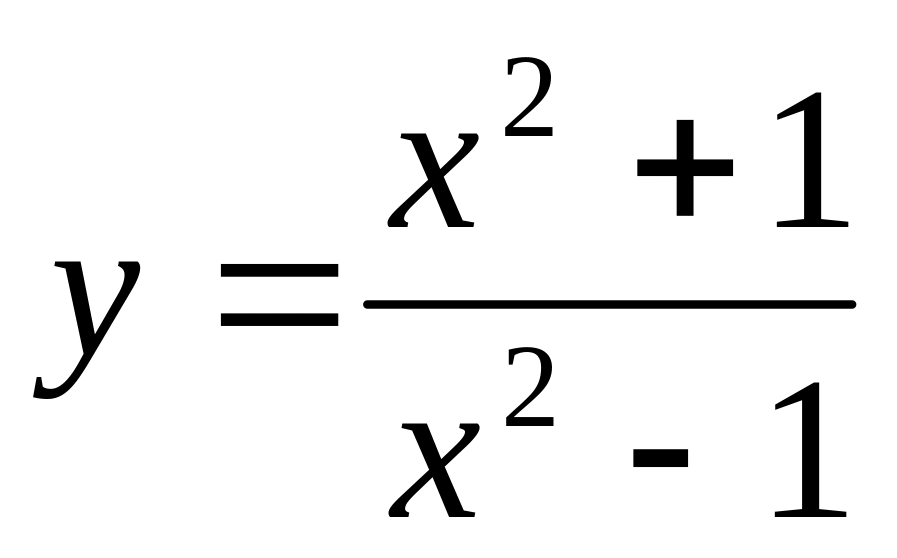и построить ее график.
Найти частные производные до второго порядка включительно ( ) заданной функции:
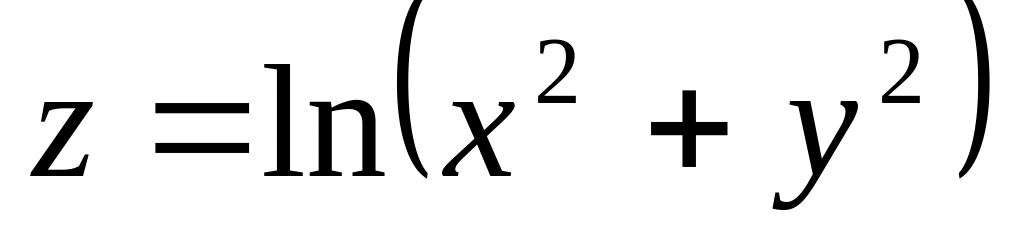
Найти градиент функции
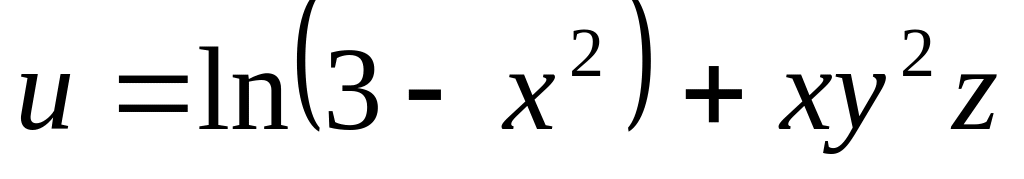в точке
Найти производную функции в точке по направлению к точке
Найти производные и функции
,где
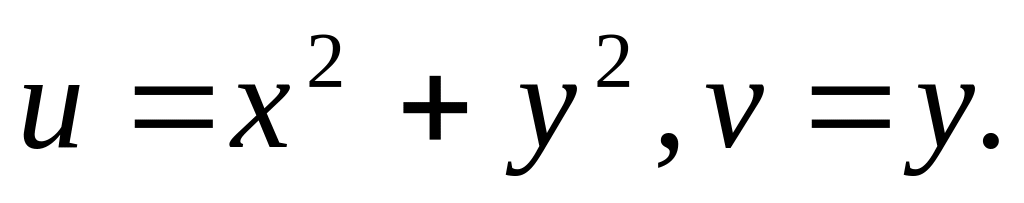
Найти уравнения касательной плоскости и нормали к поверхности
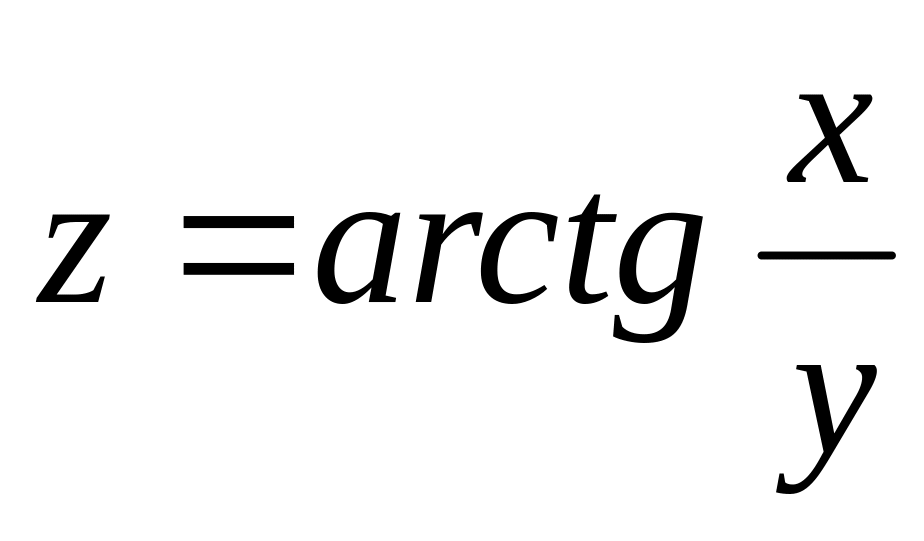в заданной точке
Найти точки экстремума функции
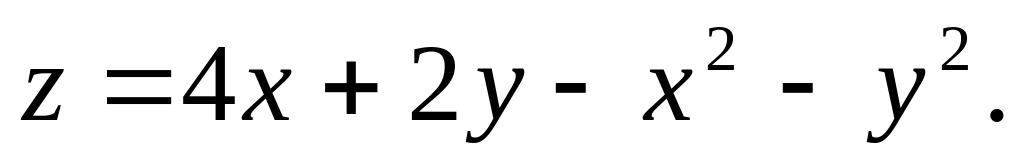
Вариант № 6.
Решить систему уравнений: а) по формулам Крамера; б) методом Гаусса; в) методом обратной матрицы
3 x + 4y + 2z = 8,
2x - y - 3z = -1,
x + 5y + z = 0.
Даны координаты вершин пирамиды А1А2А3А4 : А1(1;8;2), А2(5;2;6), А3(5;7;4), А4(4;10;9).
Найти: 1)длину вектора А1А2;
2)угол между векторами А1А2 и А1А4;
3)площадь грани А1А2А3;
4)объем пирамиды;
5)уравнение прямой А1А2.
Даны вершины А(7;-4), В(3;-7), С(-2;5) треугольника АВС. Требуется найти:
а) длину стороны АВ; б) уравнение стороны АВ;
в) уравнение медианы ВЕ, проведенной из вершины В;
г) уравнение высоты CD, проведенной из вершины С;
д) длину h высоты CD; е) площадь треугольника АВС. Сделать чертеж.
Составить уравнение линии, расстояние каждой точки которой от точки А(3; 0) вдвое меньше
расстояния от точки В(26; 0).
Линия задана уравнением r = 1/(2 + 2cos) в полярной системе координат. Требуется: построить линию по точкам, начиная от =0 до =2 и придавая значения через промежуток /8; найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;по полученному уравнению определить вид линии.
Дано комплексное число
Требуется:
а) записать число z в алгебраической и тригонометрической формах;
б) найти все корни уравнения a3 + z = 0.
Найти пределы функций, не пользуясь правилом Лопиталя.
1)
2)
3)
4)
Найти производные следующих функций.
1)
2)
3)
4)
5)
Найти 1)
2)
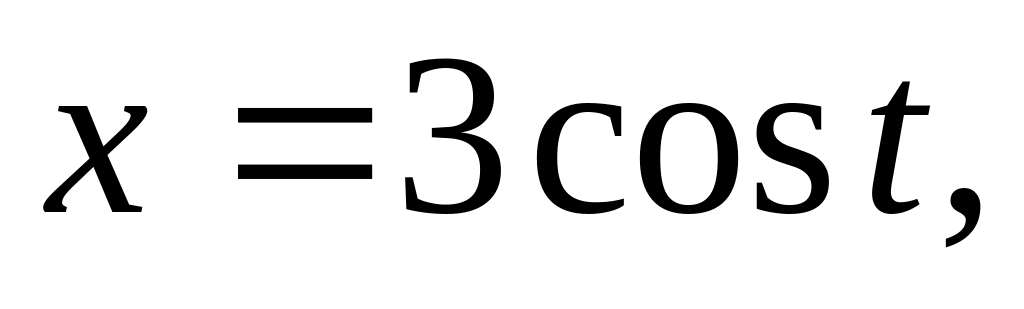
Найти приближенное значение sin62° с помощью дифференциала соответствующей функции.
Найти наибольшее и наименьшее значения функции y = 3 – х2 на отрезке
.
Исследовать методами дифференциального исчисления функцию
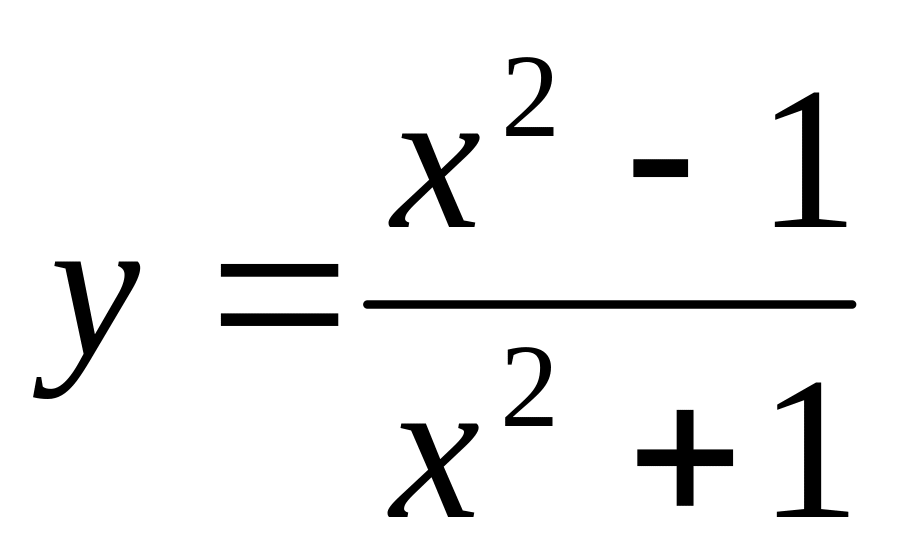и построить ее график.
Найти частные производные до второго порядка включительно ( ) заданной функции:
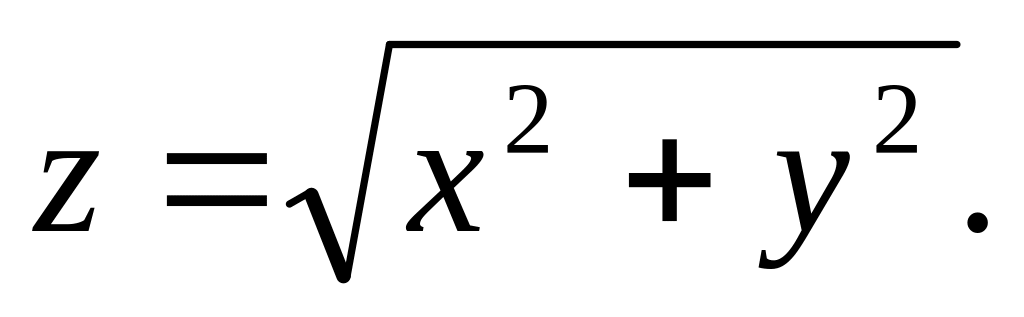
Найти градиент функции
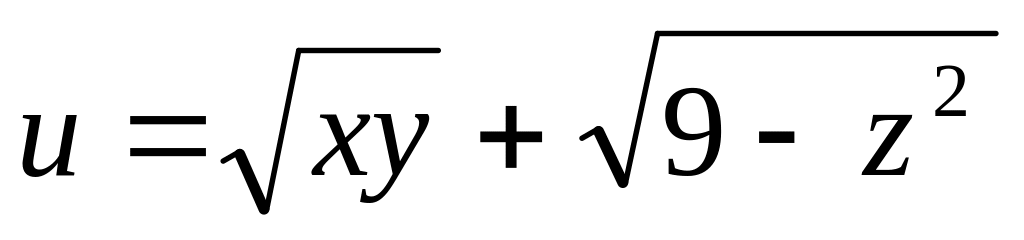в
точке
Найти производную функции в точке по направлению к точке
Найти производные и функции
,где
Найти уравнения касательной плоскости и нормали к поверхности
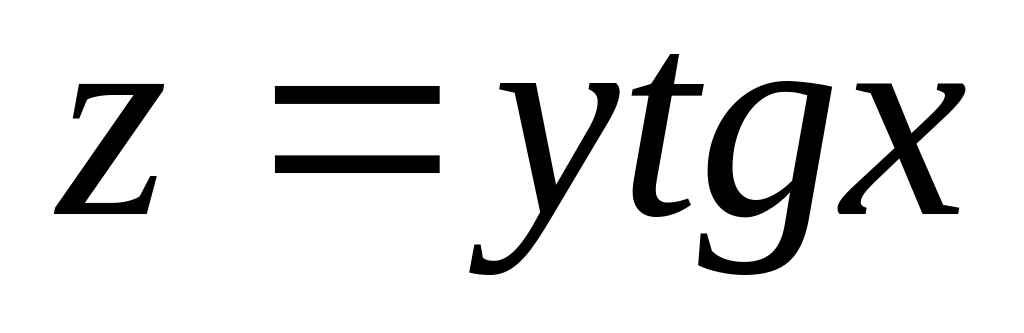в
заданной точке
Найти точки экстремума функции
