
- •Тема: «Відсоткові розрахунки»
- •Збільшилась на 10%;
- •Тема: «Функції, їх властивості і графіки»
- •Тема: «Перетворення виразів зі степенями та коренями»
- •Тема: «Перетворення логарифмічних виразів»
- •Тема: «Ірраціональні, показникові та логарифмічні рівняння»
- •Тема: «Показникові, логарифмічні та ірраціональні нерівності»
- •Тема: «Перетворення тригонометричних виразів»
- •Тема: «Тригонометричні рівняння»
- •Тема: «Вектори і координати у просторі»
- •Тема: «Основи стереометрії»
- •Тема: «Похідна та її застосування»
- •Для функції знайдіть .
- •Тема: «Інтеграл і його застосування»
- •Тема: «Многогранники. Об’єми і площі поверхонь многогранників»
- •Тема: «Тіла обертання. Об’єми і площі поверхонь тіл обертання»
- •Тема: «Елементи комбінаторики і теорії ймовірностей»
- •У школі 60% учнів займаються в спортивних секціях, з них 20% співають у хорі. Скільки відсотків учнів школи і займаються у спортивних секціях, і співають у хорі?
Тема: «Тіла обертання. Об’єми і площі поверхонь тіл обертання»
Знайдіть об’єм циліндра, у якого радіус основи дорівнює 4 см, а висота – 5 см.
16π см3;
100π см3;
40π см3;
80π см3.
Висота конуса дорівнює 6 см, а твірна – 10 см. Знайдіть радіус конуса.
4 см;
8 см;
16 см;
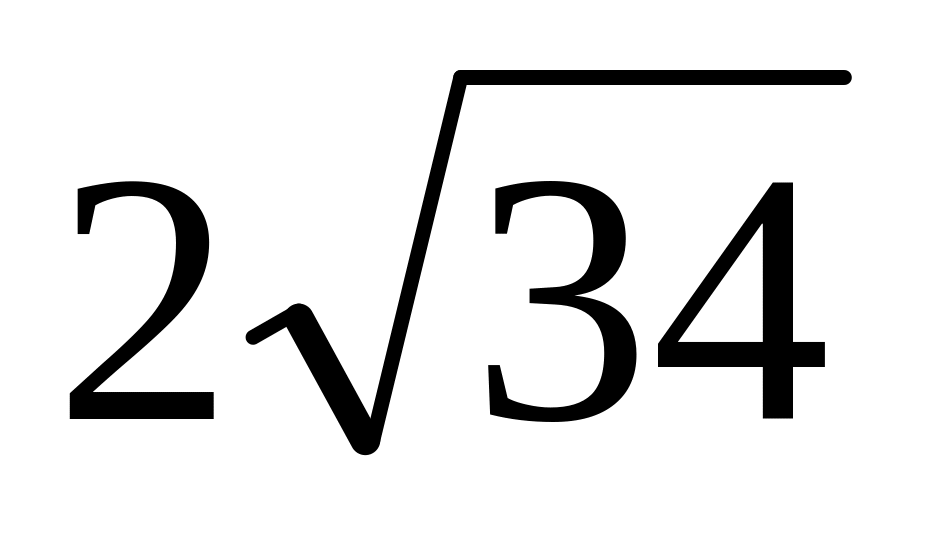 см.
см.
Радіус основи циліндра дорівнює 3 см, а висота – 8 см. Знайдіть діагональ осьового перерізу циліндра.
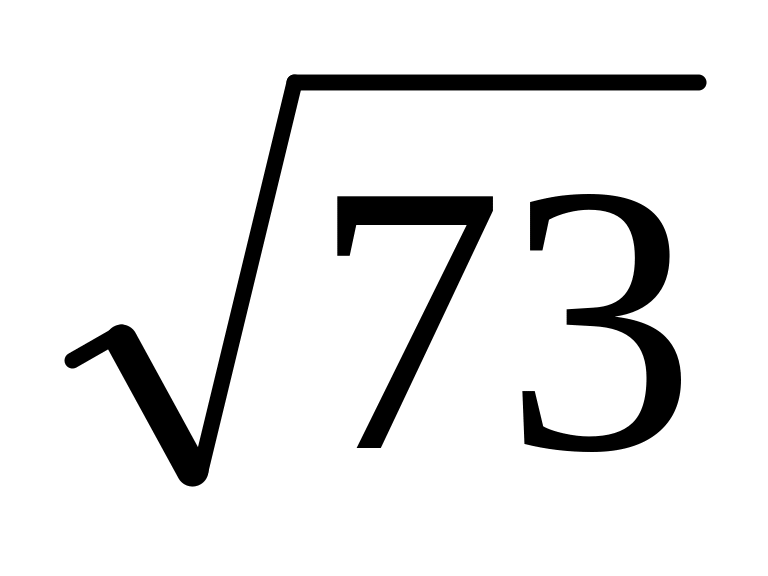 см;
см;10 см;
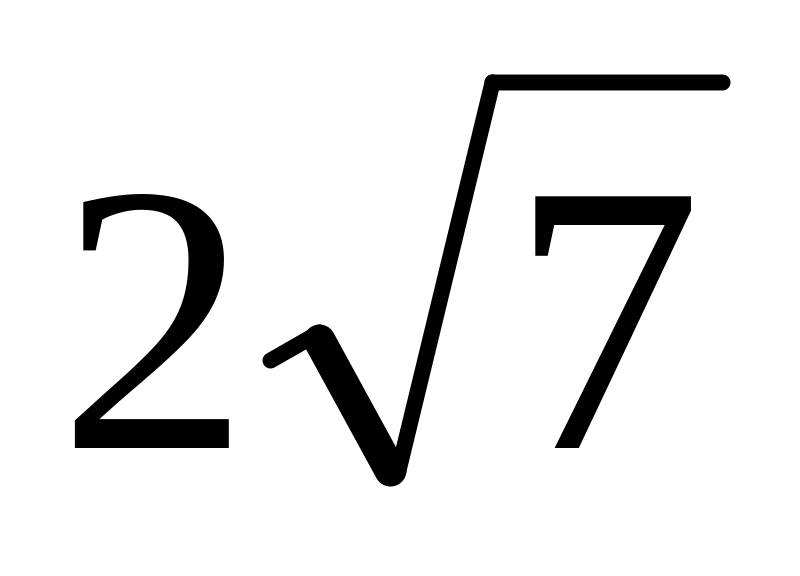 см;
см;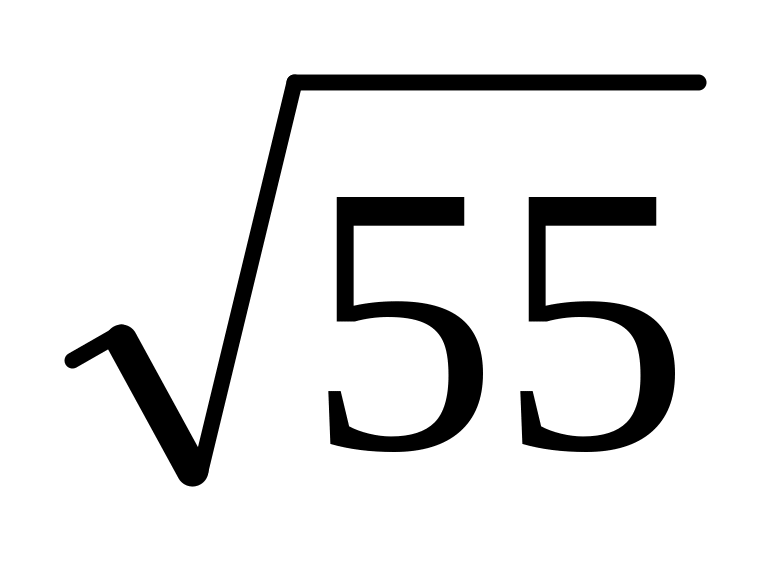 см.
см.
Чому дорівнює висота циліндра, об’єм якого становить 24π см3, а радіус основи дорівнює 2 см?
 см;
см;4 см;
6 см;
12 см.
На відстані 6 см від центра сфери проведено переріз, що перетинає сферу по колу, довжина якого дорівнює 16π см. Знайдіть площу сфери.
А)100π см2;
Б) 256π см2;
В) 400π см2;
Г) 800π см2;
Твірна конуса дорівнює 8 см і утворює кут 60º із висотою. Знайдіть площу осьового перерізу конуса.
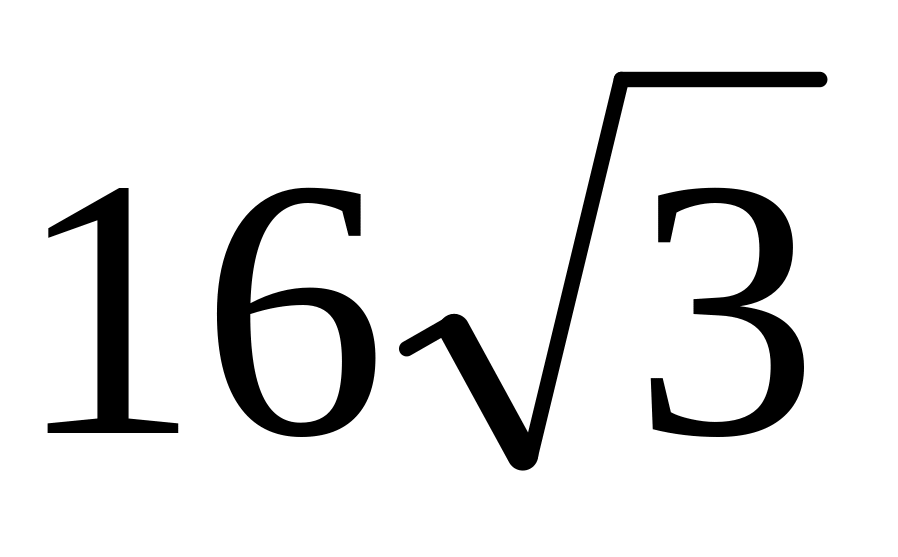 см2;
см2;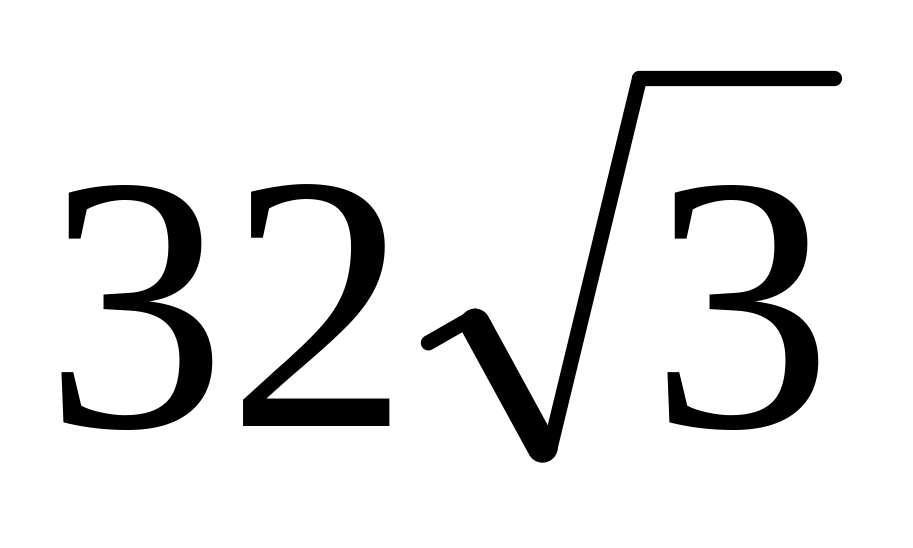 см2;
см2;32 см2;
інша відповідь.
Прямокутник зі сторонами 5 см і 6 см обертається навколо більшої сторони. Знайдіть довжину діаметра утвореного циліндра.
5 см;
10 см;
6 см;
12 см.
Чому дорівнює об’єм конуса, радіус основи якого
 ,
а висота дорівнює радіусу основи?
,
а висота дорівнює радіусу основи?
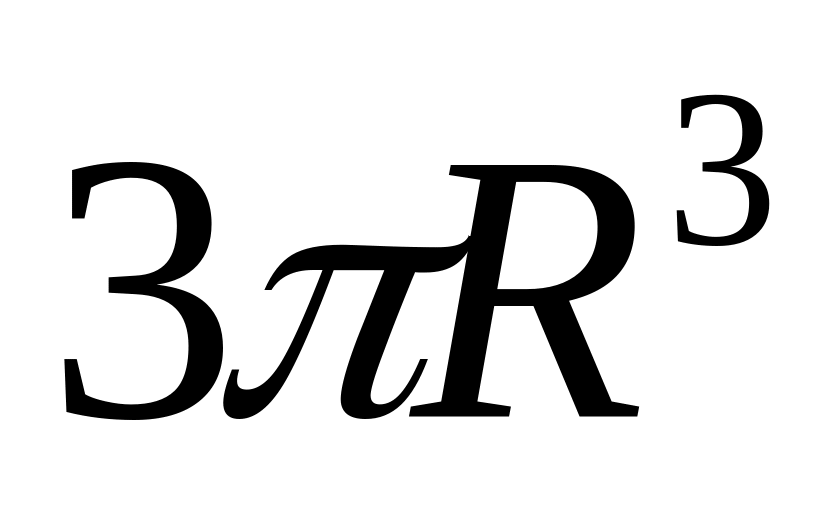 ;
;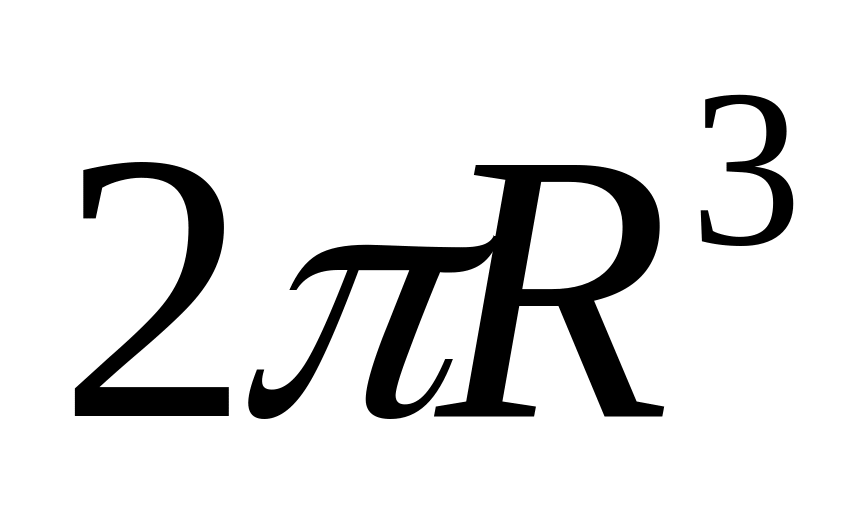 ;
;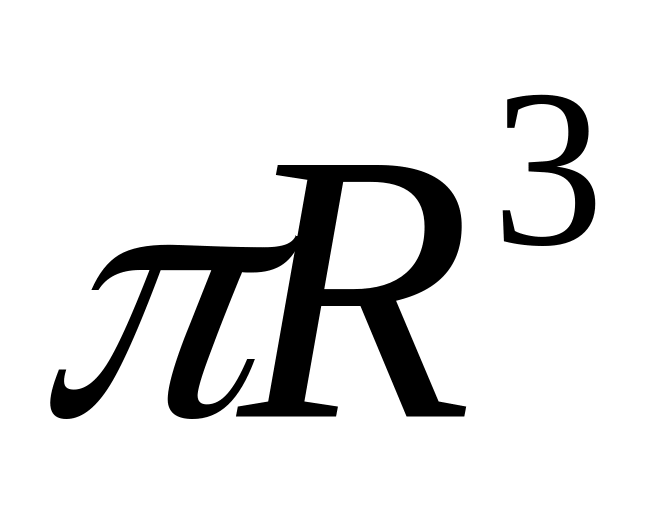 ;
; .
.
Об’єм циліндра дорівнює 250π см3, а його висота – 10 см. Знайдіть площу основи циліндра.
А) 25π см2;
Б) 5π см2;
В) 10π см2;
Г) 15π см2.
Діагональ осьового перерізу циліндра дорівнює
 см і утворює з площиною основи кут 45°.
Знайдіть площу повної поверхні циліндра.
см і утворює з площиною основи кут 45°.
Знайдіть площу повної поверхні циліндра.
96π см2;
48π см2;
24π см2;
64π см2.
Радіус основи конуса дорівнює 2 см, а твірна – 3 см. Знайдіть площу бічної поверхні конуса.
2π см2;
4π см2;
6π см2;
9π см2.
Перерізом кулі площиною, яка проведена на відстані 4 см від центра, є круг площею 9
 см2.
Знайдіть об’єм кулі.
см2.
Знайдіть об’єм кулі.
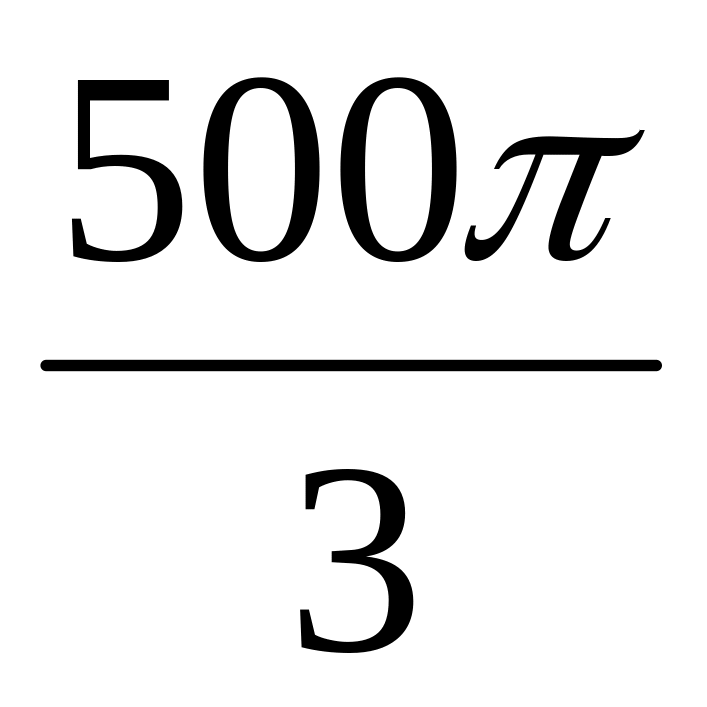 см3;
см3;125π см3;
600π см3;
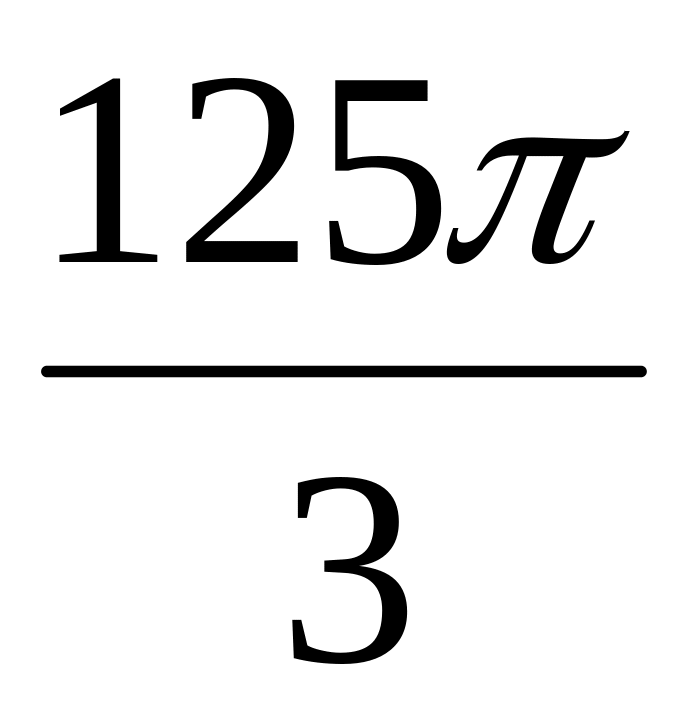 см3.
см3.
Обчисліть об’єм циліндра, висота якого дорівнює 6 см., а діаметр основи – 4 см.
А) 24π см3;
Б) 8π см3;
В) 4π см3;
Г) 12π см3.
Знайдіть площу поверхні кулі, діаметр якої дорівнює 8 см.
36π см2;
256π см2;
16π см2;
64π см2.
Радіус сфери дорівнює 6 см. Якою не може бути відстань між деякими двома точками сфери?
5 см;
11 см;
12 см;
13 см.
Точка А – деяка точка простору. Яку геометричну фігуру утворюють усі точки простору, відстань від яких до точки А не більша, ніж 6 см?
коло;
круг;
сферу;
кулю.
Площа основи конуса дорівнює 9π см2, а його об’єм - 12π см3. Знайдіть висоту конуса.
2 см;
12 см;
4 см;
8 см.
Осьовий переріз конуса – прямокутний трикутник із гіпотенузою 8 см. Знайдіть висоту конуса.
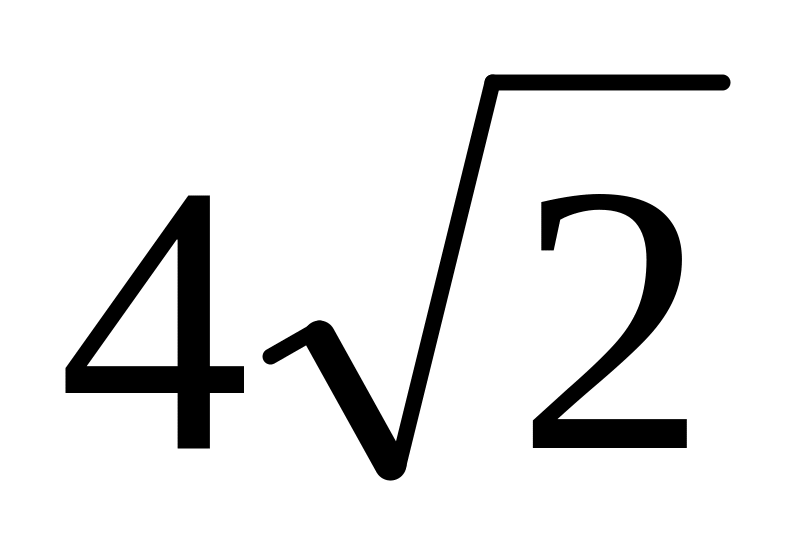 см;
см;4 см;
8 см;
інша відповідь.
Обчисліть площу бічної поверхні циліндра, осьовим перерізом якого є квадрат зі стороною 8 см.
32π см2;
64π см2;
128π см2;
256π см2.
Діагональ осьового перерізу циліндра дорівнює 17 см, а висота – 15 см. Знайдіть об’єм циліндра.
А) 960π см3;
Б) 120π см3;
В) 255π см3;
Г) 240π см3.
Прямокутний трикутник з катетом 4 см і гіпотенузою 5 см обертається навколо даного катета. Знайдіть площу повної поверхні утвореного конуса.
100π см2;
80π см2;
32π см2;
24π см2.
Обчисліть об’єм циліндра, радіус основи якого дорівнює 7 см, а твірна – 5 см.
35π см3;
175π см3;
70π см3;
245π см3.
Діаметр циліндра дорівнює 8 см, а висота – 15 см. Знайдіть об’єм циліндра.
960π см3;
120π см3;
255π см3;
240π см3.
Об’єм першої кулі у 27 разів більший за об’єм другої кулі. Чому дорівнює радіус першої кулі, якщо радіус другої кулі дорівнює 1 см?
3 см;
6 см;
9 см;
27 см.
Осьовий переріз циліндра – квадрат, площа якого дорівнює 36 см2. Знайдіть радіус основи циліндра.
9 см;
3 см;
6 см;
12 см.
Обчисліть об’єм кулі з радіусом 3см.
36π см3;
9π см3;
108π см3;
54π см3.
Обчисліть площу бічної поверхні конуса, радіус основи якого дорівнює 8 см, а твірна – 12 см.
32π см2;
48 см2;
48π см2;
96π см2.
Діагональ осьового перерізу циліндра дорівнює 4 см і утворює кут 450 з основою циліндра. Знайдіть радіус циліндра.
8 см;
см;
4 см;
2 см.
Обчисліть об’єм конуса, висота якого дорівнює 6 см, а радіус основи – 5 см.
50π см3;
150π см3;
30π см3;
10π см3.
Діаметр кулі дорівнює 8 см. Точка А належить дотичній площині до кулі і знаходиться на відстані 3 см від точки дотику кулі і площини. Знайдіть відстань від точки А до центра кулі.
см;
см;
19 см;
5 см.
Радіус основи циліндра дорівнює 3 см, а висота – 5 см. Знайдіть площу бічної поверхні циліндра.
15π см2;
30π см2;
75π см2;
45π см2.
Чому дорівнює об’єм циліндра, діаметр основи якого дорівнює 6 см, а твірна – 7 см?
21π см3;
63π см3;
42π см3;
252π см3.
Твірна циліндра дорівнює 12 см, а діагональ осьового перерізу – 13 см. Знайдіть діаметр основи циліндра.
А) 10 см;
Б) 5 см;
В) 2,5 см;
Г) 6 см.
Чому дорівнює радіус кулі, об’єм якої становить 36π см3?
6 см;
3 см;
9 см;
4 см.
Прямокутник зі сторонами 3 см і 4 см обертається навколо меншої сторони. Знайдіть довжину твірної утвореного циліндра.
8 см;
4 см;
6 см;
3 см.
Чому дорівнює площа бічної поверхні циліндра, діаметр основи якого дорівнює 4 см, а твірна – 9 см?
36π см2;
72π см2;
12π см2;
24π см2.
Радіус однієї кулі у 2 рази більший за радіус другої кулі. Чому дорівнює об’єм кулі більшого радіуса, якщо об’єм кулі меншого радіуса дорівнює 1 см3?
2 см3;
4 см3;
6 см3;
8 см3.
Точка А – деяка точка простору. Яку геометричну фігуру утворюють усі точки простору, віддалені від точки А на відстань 5 см?
А) коло;
Б) круг;
В) кулю;
Г)сферу.
Обчисліть об’єм циліндра, осьовим перерізом якого є квадрат зі стороною 8 см.
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() ;
;
Г)
![]()
Обчисліть об’єм циліндра, радіус основи якого дорівнює 9 см, а твірна 4 см.
А)
![]() ;
;
Б)
![]() ;
;
В)
![]() ;
;
Г)
![]()
Висота конуса дорівнює 6 см, а твірна – 10 см. Знайдіть радіус конуса.
4 см;
8 см;
16 см;
см.
Чому дорівнює радіус сфери, площа поверхні якої становить 100 см2?
100 см;
50 см;
5 см;
20 см.
Обчисліть об’єм кулі радіусом 6 см.
А) ;
Б)
![]() ;
;
В)
Г)
![]()
Обчисліть площу бічної поверхні конуса, радіус основи якого дорівнює 3 см, а твірна у 3 рази довша за радіус?
27π см2;
81π см2;
12π см2;
30π см2.
Висота конуса дорівнює 9 см, а його об’єм -
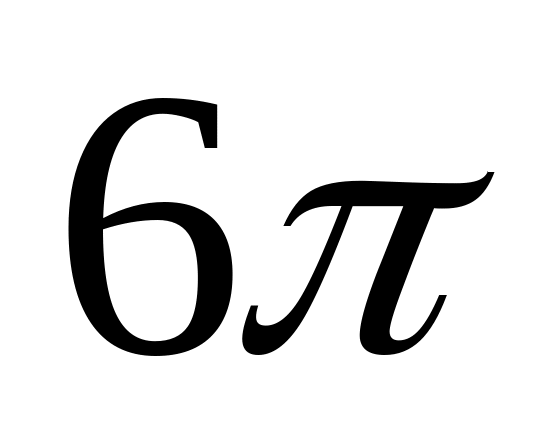 см3.Чому
дорівнює площа основи конуса?
см3.Чому
дорівнює площа основи конуса?
А) 2 см2;
Б) 2π см2;
В) 3π см2;
Г) 6 см2.
Висота циліндра дорівнює 6 см, а його об’єм – 18 см3. Чому дорівнює площа основи циліндра?
 см2;
см2;3/π см2;
3 см2;
12 см2.
Обчисліть площу бічної поверхні конуса, твірна якого дорівнює 10 см, а радіус основи – 8 см.
А) 40π см2;
Б) 80π см2;
В) 40 см2;
Г) 80 см2.
