2.2. Модуль 2. Сетевое планирование и другие модели управления
Практическое занятие 4
Цель: закрепление теоретических знаний, овладение навыками сравнения различных прогнозирующих трендов и проведение расчетов ошибки прогноза.
4.1. Применение метода наименьших квадратов
Представив в графическом виде данные, можно с помощью метода наименьших квадратов подобрать линию, в наибольшей степени соответствующую полученным данным и определить прогнозную величину исследуемого признака.
Рассмотрим метод наименьших квадратов, который находит применение в прогнозах с использованием статистического моделирования.
Для линейного тренда
=
a+bt
система нормальных уравнений:
yt=na + bt,
(4.1)
ytt =at + bt2
Подставив в систему (4.1) имеющуюся исходную информацию (yt и t) можно рассчитать параметры прогнозирующей функции, а и b. Сомножитель n - длина временного ряда.
Пример 4.1
В таблице 4.1 представлен объем продаж онкологических препаратов на оптовой фирме (тыс. руб.) за 14 месяцев. Провести расчет параметров линейного тренда и сделать прогноз на 15, 16 и 17 месяцы.
Построить графики ряда динамики и тренда.
Таблица 4.1
-
Месяцы, t
объем продаж онкологических препаратов (тыс. руб.), yt
ytt
Линейный тренд
1
145
145,000
246,967
2
314
628,000
294,960
3
430
1290,000
342,953
4
525
2100,000
390,946
5
347
1735,000
438,939
6
295
1770,000
486,932
7
426
2982,000
534,925
8
603
4824,000
582,918
9
548
4932,000
630,911
10
598
5980,000
678,904
11
665
7315,000
726,897
12
808
9696,000
774,890
13
898
11674,000
822,883
14
825
11550,000
870,876
Итого
7427
66621,000
7824,901
Для определения численных значений констант уравнения (4.1) удобно пользоваться таблицей 4.1.
Необходимо посчитать все суммы:
t = 105, t2 = 1015, yt = 7427, yt t = 66621 ,
и подставить их в систему нормальных уравнений:
7427,0 = 14 a + b 105
66621,0 = a 105 + b 1015
найдем свободный член уравнения a =198,974 и коэффициент пропорциональности b = 47,993. Таким образом, прогнозная модель имеет вид
= 198,974 + 47,993 t
Подставляя значения t=1,2…14, получим значения линейного тренда (табл.4.1). После того как мы получили линейный тренд, можно прогнозировать развитие процесса в будущем. Для этого надо подставить в полученную формулу значения t = 15, 16, 17.
Расчеты выполним по формулам:
yt=15 = 198,974 + 47,993 15 = 918,869 тыс. руб.
yt=16 = 198,974 + 47,993 16 = 966,862 тыс. руб.
yt=17 = 198,974 + 47,993 17 = 1014,855 тыс. руб.
Нанесем полученные данные на график (рис. 4.1).
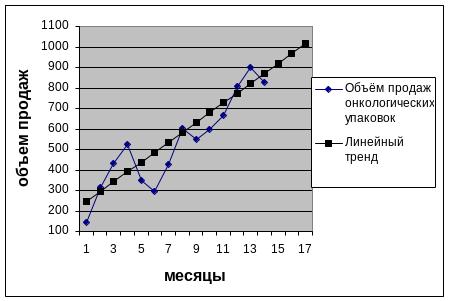
Рис. 4.1 Построение линейного тренда к исходному ряду
Из графика видно, что изменение выпуска продукции можно приблизить линейной зависимостью.
Пример 4.2
Используя исходные данные предыдущего примера (табл. 4.1) провести расчет параметров логарифмического тренда и сделать прогноз на 15, 16 и 17 месяцы. Построить графики ряда динамики и тренда.
Для нелинейных функций, например логарифмической, степенной, экспоненциальной и других процессу построения системы нормальных уравнений предшествует этап линеаризации кривой, предусматривающий переход от нелинейных связей к линейной зависимости изменения признака. С этой целью осуществляется замена переменных.
Составим
систему нормальных уравнений для
логарифмической прогнозирующей функции
=a+bln
t.
Для этого необходимо выполнить замену переменных.
Линеаризованное уравнение — yt = a + b t1 , где t1= ln t;
Система нормальных уравнений:
yt = an + b t1
yt t1 = a t1 + b t12
Сомножитель n в первом уравнении системы характеризует объем выборочной совокупности (n = 14). Определим все суммы, включенные в систему нормальных уравнений. Результаты вычислений удобно записать в специальную таблицу (табл. 4.2).
Таблица 4.2
-
Месяцы, t
объем продаж онкологических препаратов (тыс. руб.), yt
ln t
yt lnt
(lnt)2
(прогноз.)
1
145
0,000
0,000
0,000
110,195
2
314
0,693
217,648
0,480
278,167
3
430
1,099
472,403
1,207
376,425
4
525
1,386
727,805
1,922
446,140
5
347
1,609
558,475
2,590
500,215
6
295
1,792
528,569
3,210
544,397
7
426
1,946
828,958
3,787
581,753
8
603
2,079
1253,903
4,324
614,112
9
548
2,197
1204,079
4,828
642,655
10
598
2,303
1376,946
5,302
668,187
11
665
2,398
1594,600
5,750
691,284
12
808
2,485
2007,805
6,175
712,370
13
898
2,565
2303,325
6,579
731,767
14
825
2,639
2177,222
6,965
749,726
Всего: 105
7427
25,191
15251,738
53,118
7647,394
Таким образом:
t1 = ln t = 25,191; t12 = 53,118; yt = 7427; yt t1 = 15251,738.
Подставим полученные результаты в систему
7427 =14a +25,191b;
15251,738= 25,191a + 53,118b.
Решив систему, найдем константы прогнозирующей функции:
a = 110,195; b = 242,333.
Следовательно, уравнение прогноза имеет вид:
= 110,195+ 242,333 lnt
Зная параметры уравнения тренда, можно определить расчетные значения переменной для всех месяцев предпрогнозного периода. Так расчетная величина (t = 1) составляет:
yt=1 = 110,195+ 242,333 ln1 = 110,195 тыс.руб.
После того как получили логарифмический тренд, можно прогнозировать развитие процесса в будущем. Для этого надо просто подставить в формулу значения t = 15, 16, 17.
Расчеты выполним по формулам:
yt=15 = 110,195+ 242,333 ln15 = 766,44 тыс.руб.
yt=16 = 110,195+ 242,333 ln16 = 782,08 тыс.руб.
yt=17 = 110,195+ 242,333 ln17 = 796,78 тыс.руб.
Практическое занятие 5
Цель: приобрести навыки прогнозирования экономических показателей в среде Excel, на основе модели научиться выбирать одну из альтернатив, сравнение прогнозирующих функций с помощью остаточной дисперсии и других статистических показателей.