10.Марковские цепи с конечным числом состоянии и непрерывным временем

Пусть физическая система, возможные состояния которой А₁,А₂, .... , А_k может переходить из со­стояния в состояние не в определенные моменты времени, а в любой момент времени случайным образом. При этом воз­никает случайный процесс (цепь) с непрерывным временем.

Если процесс с непрерывным временем обладает отсутствием последействия, то его называют марковским случайным процессом с непрерыв­ным временем или непрерывной цепью Маркова.

Для непрерывной цепи Маркова. вероятность перехода из состояния А_i в состояние А_j в любой момент времени равна нулю. Поэтому вместо вероятности перехода Р_ij рассматривают плотность вероят­ности перехода _ij которая определяется как предел отно­шения вероятности перехода Р_ij{t} за время t из состо­яния A_i в состояние A_j; к длине промежутка t при t 0, т. е.

_ij = . (1)

Плотность вероятности _ij может быть как постоянной величиной, так и величиной, зависящей от момента времени t, с которого начинается промежуток t.

Если плотность ве­роятности перехода _ij не зависит от t, марковский процесс(цепь) называется однородным.

В дальнейшем будем пред­полагать, что рассматриваемые процессы удовлетворяют ус­ловию ординарности: в один и тот же момент времени t си­стема не может изменить свое состояние более чем один раз.

Из курса дифференциального исчисления известно, что соотношение (1) можно записать в виде Р_ij(t)=_ijt + _ij(t), где _ij(t)— бесконечно малая высшего порядка по сравнению с t. Тогда с точностью до бесконеч­но малой имеем:

P_ij(t) = _ijt, i j (2)

т. е. вероятность перехода Р_ij(t) за малое время t равна произведению плотности вероятности перехода _ij на t. По­этому _ij еще называют интенсивностью перехода системы из А_i в Aj.

Из величин _ij составим квадратную матрицу интенсивностей переходов:

 = (3)

обладающую свойствами:

1) _ij 0, i j, это следует из (2), так как P_ij(t) 0;

2) _ij 0, i=j, так как _ii = (P_ii(t) – 1);

3) = 0 действительно, (_i1 + _i2 + … _ii + … _ik)t = P_i1(t) + P_i2(t) +…+( P_ii(t) – 1) + …+ P_ik(t)) = 0.

Интенсивности переходов _ij удобно задавать на графе состояний. На графе указывают обычно интенсивности _ij >0.

Зная матрицу интенсивностей переходов или размеченный граф состояний, можно определить вероятности состояний:

p₁ (t), p₂ (t), …, p_k(t), = 1, (4)

т. е. вероятности нахождения системы в состоянии А₁, А₂, … , А_k в момент времени t. Вероятности p_i(t) как функции t удовлетворяют системе дифференциальных уравнении Колмо­горова, которая в матричной форме имеет вид

p^’(t) = p(t)  (5)

где p^’(t) = ( p₁^’(t), p₂^’(t),…, p_k^’(t)); p(t) = ( p₁(t), p₂(t),…, p_k(t)),  —

матрица интенсивностей переходов (З).

Распределение вероятностей состояний системы называется стационарным, если оно не меняется с течением времени, т. е. если

p(t) = p, (6)

где p = ( p₁, p₂, …, p_k) = const, j = 1, 2, ..., k. Дифференцируя равенство (6) по t, получим: p^’(t) = 0.

С учетом уравнения (5) приходим к выводу, что стационар­ное распределение удовлетворяет соотно­шению

p  = 0, (7)

т. е. для получения стационарного распределения достаточно в системе дифференциальных уравнений Колмогорова поло­жить p^'_j =0; j =1, 2,.., k.

Уравнения системы (7) не в матричной форме удобно вы­писывать непосредственно по размеченному графику состоя­ний в соответствии со следующим правилом:

сумма произведений _jip_i, j i для стрелок, выходящих из i-го состояния, рав­на сумме произведений _ijp_j, j i для стрелок, входящих в i-е состояние.

Задача 2. Задана матрица

интенсивностей переходов непрерывной цепи Маркова. Со­ставить размеченный граф состояний, соответствующий мат­рице ; выписать систему дифференциальных уравнений Колмогорова для вероятностей состояний; найти стационар­ное распределение вероятностей.

Решение. Размеченный граф должен иметь 3 состояния А₁, А₂, А₃. Из матрицы  находим интенсивности переходов _ij>0, i j и отмечаем их над соответствующими стрелка­ми (рис. 2). Имеем ₁₂=5, соединяем состояния А₁ и А₂ стрел­кой, направленной от А₁ к А₂, отмечая интенсивность перехода над стрелкой; ₁₃=0, следовательно, состояния А₁ и А₃ стрелкой не соединяем и т. д. Составляем

уравнения Колмогорова: положим в уравнении (5); p(t) = (p₁(t), p₂(t), p₃(t)); p^’(t) = (p₁^’(t), p₂^’(t), p₃^’(t)),

тогда

(p₁^’(t), p₂^’(t), p₃^’(t)) = (p₁(t), p₂(t), p₃(t))

умножая вектор p(t) на матрицу  будем иметь:

p₁^’(t) = - 5 p₁(t) + p₂(t) + p₃(t);

p₂^’(t ) = 5p₁(t) - p₂(t) + p₃(t);

p₃^’(t ) = -2 p₃(t).

Для нахождения стационарного распределения достаточ­но в последней дифференциальной системе положить все производные p_i^’(t ) = 0, i = 1, 2, 3. Пусть p = (p₁, p₂, p₃) есть стационарное распределение, тогда:

0 = - 5 p₁ + p₂ + p₃;

0 = 5p₁ - p₂ + p₃; (8)

0 = -2 p₃.

Решая систему, получим p₃ = 0, p₂= 5p₁. В силу уравнения (4) p₁ + p₂ + p₃ = 1,следовательно, p = ( 1/6; 5/6; 0).

Заметим, что для определения стационарного распределе­ния мы получили бы такую же систему, если бы воспользо­вались правилом, приведенным выше. Действительно, для состояния А₁ имеем 5 p_{1 =} 1 p₂ + 1 p₃ , для состояния А₂: 1 p₂ = 5p₁ + 1 p₃, для состояния A₃: 1 p₃ + 1p₃ = 0. Составляя из этих уравнений систему, убедимся, что она эквивалентна си­стеме (8).

Для многих практических случаев важно знать, как ведут себя вероятности p_i(t}, i=l, 2,..., k при большом времени работы системы, т. е. при t . Если при определенных ус­ловиях существуют предельные вероятности состояний

p_i = p_i(t), i = 1, 2, …, k, (9)

не зависящие от того, в каком состоянии система находилась в начальный момент, то это означает, что с течением времени в системе устанавливается предельный стационарный режим.

Система, для которой существуют предельные вероятно­сти, называется эргодической, а возникающий в ней случай­ный процесс эргодическим.

Выясним условия, при которых существуют предельные вероятности состояний. Введем ряд понятий.

Состояние А_i называется несущественным, если найдется такое состояние А_j что из A_i в А_j, перейти можно, а из Aj в A_i — нельзя. Состояние A_i называется существенным, если оно не является несущественным. Например, для систе­мы, граф состояний которой дан на рис. 2, состояние А₃ не­существенно (так как из него можно перейти в состояние А₁ или А₂ но обратно вернуться нельзя), состояния А₁ и A₂ — существенны. Два существенных состояния A_i и A_j назы­ваются сообщающимися, если из A_i можно попасть в A_j и из A_j в A_i. На рис. 2 представлены сообщающиеся состоя­ния A₁ и А₂.

Теорема 1. Если A_i — несущественное состояние, то

p_i(t) = 0. (10)

Смысл этой теоремы состоит в том, что в конечном итоге система выйдет из несущественного состояния A_i и больше в него не вернется.

Теорема 2. Чтобы цепь (процесс) с конечным числом состояний имела единственное стационарное распределение вероятностей, совпадающее с предельным, необходимо и до­статочно, чтобы все ее существенные состояния сообщались между собой.

Пример. В условиях задачи 2 найти предельные веро­ятности состояний.

Решение. В рассматриваемой цепи состояния A₁ и A₂ являются существенными сообщающимися состояниями, A₃ — несущественно. Следовательно, по теореме 2 предель­ное распределение совпадает со стационарным и имеет вид p = ( 1/6; 5/6; 0). Заметим, что результат p₃(t) = 0 можно было получить непосредственно из теоремы 1, так как состояние A₃ несущественно.

Пример. Задана матрица интенсивностей переходов непрерывной цепи Маркова. Составить размеченный граф со­стояний, соответствующий матрице ; составить систему диф­ференциальных уравнений Колмогорова для вероятностей состояний; найти предельное распределение вероятностей.

Дано:

Решение: Однородная цепь Маркова с конечным числом состояний A₁,A₂,…,A_k характеризуется матрицей интенсивностей переходов

,

где - интенсивность перехода цепи Маркова из состояния A_i в состояние A_j;

- вероятность перехода A_i A_j за интервал времени .

Переходы системы из состояния в состояние удобно задавать с помощью размеченного графа состояний, на котором отмечаются дуги, соответствующие интенсивностям .

Составим размеченный граф состояний для заданной матрицы интенсивностей переходов.

Пусть - вектор вероятностей , нахождения системы в состоянии A_j в момент t. Очевидно, что и . Тогда по правилу дифференцирования векторной функции скалярного аргумента получим . Вероятности удовлетворяют системе дифференциальных уравнений Колмогорова (СДУК), которая в матричной форме имеет вид

(6)

,

Если в начальный момент система находилась в состоянии A_j, то СДУК следует решать при начальных условиях

(7)

Совокупность СДУК (6) и начальных условий (7) однозначно описывает однородную цепь Маркова непрерывным временем и конечным числом состояний.

Составим СДУК для заданной цепи Маркова. Поскольку k=3, то j=1,2,3. Из соотношения (6) получим

Отсюда будем иметь:

Последнее условие называется нормировочным.

Распределение вероятностей по состояниям называется стационарным, если оно не меняется с течением времени, то есть , где p_j=const, j=1,2,…,k.

Отсюда . Тогда из СДУК (6) получаем систему для нахождения стационарного распределения , где .

Для данной задачи из СДУК будет иметь

Из нормировочного условия получим

Ответ: предельное распределение имеет вид .

Пример. Определить, существует ли стационарный режим для марковского случайного процесса, размеченный граф состояний которого изображен на рисунке. Если стационарный режим существует, то найти стационарное распределение вероятностей.

Указание. Проведите классификацию состояний системы и примените следствия из теоремы Маркова.

а) Состояние 6 - существенное. Остальные - несущественные состояния. Поэтому единственное стационарное распределение совпадает с предельным.

Для несущественных состояний предельные вероятности равны нулю. Учитывая, что сумма всех вероятностей = 1 получим искомое стационарное распределение:

б) Несущественные состояния 1, 2, 6. Состояния 3, 4, 5 - существенные сообщающиеся поэтому единственное стационарное распределение совпадает с предельным.

Приравнивая к каждую из строк-уравнений к 0 и учитывая, что сумма вероятностей = 1 получим:

11.Процесс гибели и размножения

Процессом гибели и размножения называется марковская цепь, размеченный граф состояний которой изображен на рис. 3. Здесь ₀, ₁, …,_k-1— интенсивности переходов си­стемы из состояния в состояние слева направо; ₁, ₂,…, _k—

Рис. 3

интенсивности переходов справа налево. Очевидно, все со­стояния A₀, A₁, ..., A_k являются существенными сообщающи­мися состояниями. Следовательно, в силу теоремы 2 сущест­вует предельное распределение вероятностей состояний, ко­торое имеет вид:

p₀ = ;

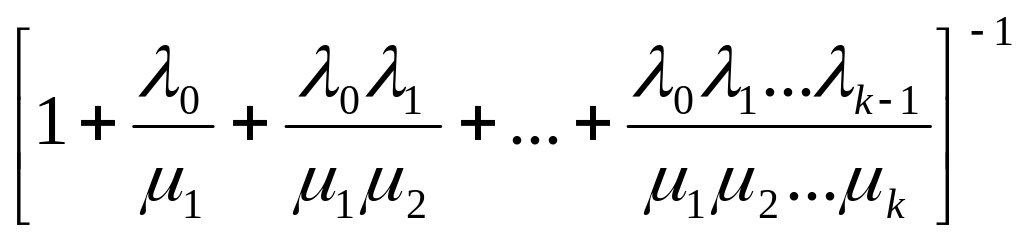p₁ = p₀; p₂ = p₀; … ; p_k = p₀. (11)

12.Системы массового обслуживания и их классификация.

Математический аппарат для изучения закономерностей функционирования систем, удовлетворяющих массовый спрос, и образования очередей в такого рода системах называется теорией массового обслуживания.

Методы теории массового обслуживания все более широ­ко применяются на транспорте для расчета рациональной ор­ганизации подачи вагонов под разгрузку и погрузку, для рас­чета мощностей пунктов текущего ремонта вагонов, для вы­бора рационального числа кассовых аппаратов на вокзалах и станциях метрополитена. Поэтому современному инженеру железнодорожного транспорта необходимо знать основы тео­рии массового обслуживания.

Заявкой (требованием) назовем спрос на удовлетворение какой-либо потребности. Далее будем подразумевать, что все заявки однотипные. Удовлетворение спроса назовем об­служиванием заявки.

Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания каких-либо заявок, поступающих в нее в случайные моменты време­ни. Устройство, непосредственно обслуживающее заявку, на­зывается каналом обслуживания. СМО может содержать одно такое устройство, тогда она называется одноканальной. Если СМО содержит несколько обслуживающих устройств, то она называется многоканальной.

Поступление заявки в СМО назовем событием. Последо­вательность событий, состоящих в поступлении заявок в СМО, назовем входящим потоком заявок. Последовательность собы­тий, состоящих в выходе заявок из СМО, назовем выходящим потоком заявок.

В зависимости от поведения заявки в СМО различают СМО с отказами и СМО с очередью (или ожиданием). В СМО с отказами заявка, поступившая в момент занятости всех каналов, получает отказ и покидает СМО. В СМО с оче­редью (или ожиданием) заявка, поступившая в момент за­нятости всех каналов, становится в очередь и ожидает осво­бождения одного из каналов обслуживания.

Возможны СМО смешанного типа. Например, СМО с ог­раниченной очередью. В такой СМО заявка становится в оче­редь при занятости всех каналов, если очередь невелика, скажем, не достигла длины т. Если все т мест в очереди за­няты, заявка покидает СМО. К СМО смешанного типа отно­сятся СМО с ограниченным временем ожидания. Заявка, по­ступившая в момент занятости всех каналов, становится в очередь, но может уйти из СМО необслуженной, если время ожидания слишком велико.

СМО с очередью (или с ожиданием) могут быть открыто­го и замкнутого типа. В открытых СМО интенсивность по­ступающего на нее потока заявок не зависит от состояния самой СМО, так как круг «клиентов» (поступающих заявок) практически не ограничен. Примерами таких СМО являются вокзальные кассы, метрополитен, телевизионные ателье больших городов и т. д. В СМО с очередью замкнутого типа об­служивается ограниченный круг «клиентов», поэтому интен­сивность потока заявок существенно зависит от состояния си­стемы. Примерами таких СМО являются различные ремонт­ные системы в автопарках, цехах и т. д.

СМО с очередью и смешанного типа различаются также по дисциплине обслуживания; обслуживаются ли заявки в порядке поступления, или в случайном порядке, или есть заявки, которые обслуживаются вне очереди (СМО с приорите­том).