2. Операції оцінювання
Оцінювання речовинних виражень
В Maple є наступні команди оцінювання дійсних виразів:
frac(expr) – обчислення дробової частини виразу expr;
trunc(expr) – обчислення цілої частини виразу expr;
round(expr) – округлення виразу expr;
Оцінювання комплексних виразів
Дійсну й мниму частини комплексного виразу z=x+iy можна знайти за допомогою команд Re(z) і Im(z). Наприклад:
> z:=3+I*2:
> Re(z);Im(z);
3, 2
Якщо z=x+iy, то комплексний спряжений йому вираз w=z*=x–iy можна знайти за допомогою команди conjugate(z). Продовження попереднього прикладу:
w:=conjugate(z);
w:=3–2 I
Модуль і аргумент комплексного виразу z можна знайти за допомогою команди polar(z), яку необхідно попередньо викликати зі стандартної бібліотеки командою readlib. Наприклад:
> readlib(polar): polar(I);
polar
У
рядку виводу в дужках через кому
зазначений модуль числа i,
дорівнює одиниці і його аргументу,
рівний
.
Якщо комплексне число дуже складне або містить параметри, то команди Re(z) і Im(z) не дають необхідного результату. Одержати дійсну й мниму частини комплексного виразу z можна, якщо використовувати команду перетворення комплексних виразів evalc(z). Наприклад:
> z:=ln(1-I*sqrt(3))^2;
> evalc(Re(z)); evalc(Im(z));
Приклад 2.
Дано число а=57/13. Знайти його цілу частину x і дробову частину y і переконатися, що a=x+y. Наберіть:
> a:=57/13:
> y:=frac(a);
> x:=trunc(a);
4
> x+y;
Дано комплексне число
.
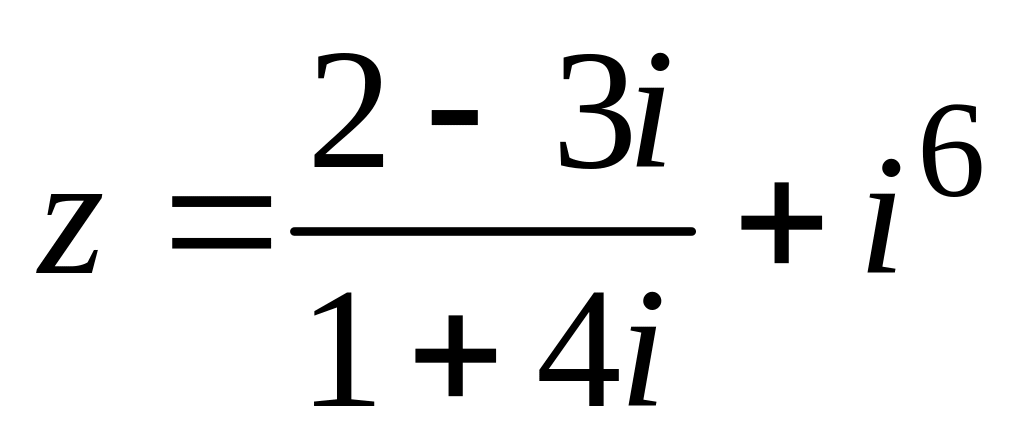Знайти його дійсну й мниму частини, а
потім комплексно сполучене йому число
w і
переконатися, що w+z=2Re(z).
У командному рядку наберіть:
> z:=(2-3*I)/(1+4*I)+I^6:
> Re(z); Im(z);
> w:=conjugate(z);
> z+w;
Знайти модуль і аргумент комплексного числа
й обчислити z4.
Наберіть:
> z:=-1-I*sqrt(3):
> readlib(polar): polar(z);
polar
Чому дорівнює модуль і аргумент цього числа?
> evalc(z^4);
3. Розв’язання рівнянь
Розв’язання звичайних рівнянь
Для розв’язання рівнянь в Maple існує універсальна команда solve(eq,x), де eq – рівняння, x – змінна, щодо якої рівняння треба розв’язати. У результаті виконання цієї команди в рядку виводу з'явиться вираз, що є розв’язанням даного рівняння. Наприклад:
> solve(a*x+b=c,x);
Якщо рівняння має кілька розв’язків, які вам знадобляться для подальших розрахунків, то команді solve варто привласнити яке-небудь ім'я name. Звертання до якого-небудь k-ого рішення даного рівняння робиться вказівкою його ім'я з номером розв’язання k у квадратних дужках: name[k]. Наприклад:
> x:=solve(x^2-a=0,x);
> x[1];
> x[2];
> x[1]+x[2];
0
Розв’язання систем рівнянь
Системи рівнянь вирішуються за допомогою такої ж команди solve({eq1,eq2,…},{x1,x2,…}), тільки тепер у параметрах команди треба вказувати в перших фігурних дужках через кому рівняння, а в других фігурних дужках перераховуються через кому змінні, щодо яких потрібно розв’язати систему. Якщо вам буде необхідно для подальших обчислень використовувати отримані розв’язання рівнянь, то команді solve варто привласнити яке-небудь ім'я name. Потім виконується присвоєння команда assign(name. Після цього над розв’язаннями можна буде робити математичні операції. Наприклад:
> s:=solve({a*x-y=1,5*x+a*y=1},{x,y});
s:={
}
> assign(s); simplify(x-y);
Чисельне розв’язання рівнянь
Для чисельного розв’язання рівнянь, у тих випадках, коли трансцендентні рівняння не мають аналітичних розв’язків, використовується спеціальна команда fsolve(eq,x), параметри якої такі ж, як і команди solve. Наприклад:
> x:=fsolve(cos(x)=x,x);
x:=.7390851332
Розв’язання рекурентних і функціональних рівнянь.
Команда rsolve(eq,f) дозволяє розв’язати рекурентне рівняння eq для цілої функції f. Можна задати деяку початкову умову для функції f(n), тоді отримаємо часний розв’язок даного рекурентного рівняння. Наприклад:
> eq:=2*f(n)=3*f(n-1)-f(n-2);
> rsolve({eq,f(1)=0,f(2)=1},f);
Універсальна команда solve дозволяє розв’язувати функціональні рівняння, наприклад:
> F:=solve(f(x)^2-3*f(x)+2*x,f);
F:= proc(x) RootOf(_Z^2 - 3*_Z + 2*x) end
У результаті отримаємо розв’язок в неявному виді. Однак Maple може працювати з такими розв’язками. Неявний розв’язок функціонального рівняння можна спробувати перетворити в яку-небудь елементарну функцію за допомогою команди convert. Продовжуючи наведений вище приклад, можна одержати розв’язок в явному виді:
> f:=convert(F(x),radical);
Розв’язання тригонометричних рівнянь
Команда solve, застосована для розв’язання тригонометричного рівняння, видає тільки головні розв’язки, тобто розв’язок в інтервалі [0,2]. Для того, щоб одержати всі розв’язки, варто попередньо ввести додаткову команду _EnvAllSolutions:=true. Наприклад:
> _EnvAllSolutions:=true:
> solve(sin(x)=cos(x),x);
~
В
Maple
символ _Z~
позначає константу цілого типу,
тому розв’язок даного
рівняння у звичній формі має вигляд
,
де n
– цілі числа.
Розв’язання трансцендентних рівнянь
При розв’язанні трансцендентних рівнянь для одержання розв’язків в явному виді перед командою solve треба ввести додаткову команду _EnvExplicit:=true. Приклад розв’язання складної системи трансцендентних рівнянь і спрощення виду розв’язків:
> eq:={ 7*3^x-3*2^(z+y-x+2)=15, 2*3^(x+1)+
3*2^(z+y-x)=66, ln(x+y+z)-3*ln(x)-ln(y*z)=-ln(4) }:
> _EnvExplicit:=true:
> s:=solve(eq,{x,y,z}):
> simplify(s[1]);simplify(s[2]);
{x=2, y=3, z=1}, {x=2, y=1, z=3}
Приклад 3.
Знайти всі розв’язки системи рівнянь
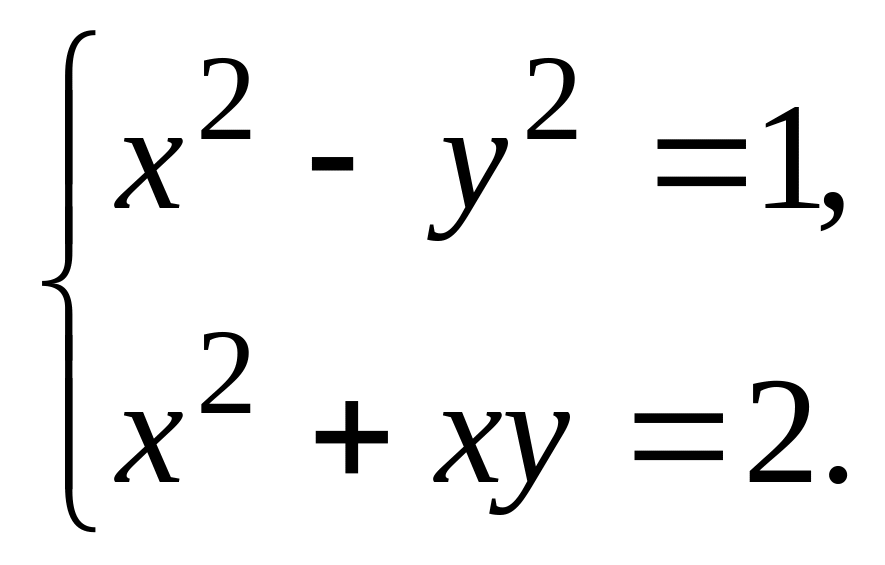
Наберіть:
> eq:={x^2-y^2=1,x^2+x*y=2};
> _EnvExplicit:=true:
> s:=solve(eq,{x,y});
,
Тепер знайдіть суму двох наборів розв’язків. Наберіть:
> x1:=subs(s[1],x): y1:=subs(s[1],y):
x2:=subs(s[2],x): y2:=subs(s[2],y):
> x1+x2; y1+y2;
Чому дорівнюють ці суми розв’язків?
Чисельно розв’яжіть рівняння
.
Наберіть:
> x=fsolve(x^2=cos(x),x);
x=.8241323123
Знайдіть функцію f(x), що задовольняє рівнянню
.
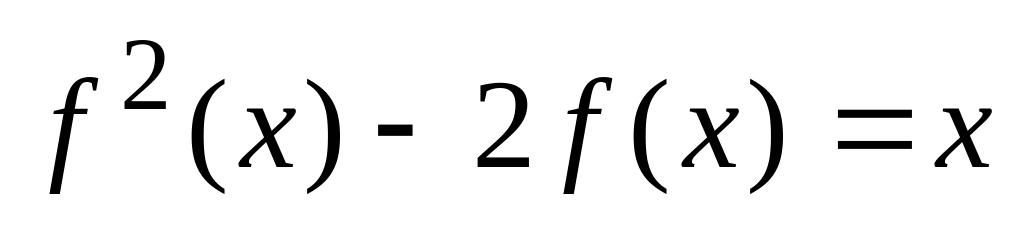Наберіть:
> F:=solve(f(x)^2-2*f(x)=x,f);
F:= proc(x) RootOf(_Z^22*_Zx) end
> f:=convert(F(x), radical);
Знайдіть всі розв’язки рівняння
.
Наберіть:
> _EnvAllSolutions:=true:
> solve(5*sin(x)+12*cos(x)=13,x);
~