2. Арифметичні операції. Цілі й раціональні числа, константи в Maple

Математичні константи й арифметичні операції.

Основні математичні константи:

Pi – число ; I – мнима одиниця i; infinity – нескінченність; Gamma – константа Ейлера; true, false – логічні константи, що позначають істинність і хибність висловлення.

Знаки арифметичних операцій:

+ - додавання; – - віднімання;

* - добуток; / - частка;

^ - піднесення до степеня; ! - факторіал.

Знаки порівняння: <, >, >=,<=, <>, =.

Комплексні, цілі й раціональні числа.

Числа в Maple бувають дійсні (real) і комплексні (compleх). Комплексне число записується в алгебраїчній формі z=x+iy, і в командному рядку такий запис повиннен виглядати так:

> z:=x+I*y;

Дійсні числа поділяються на цілі й раціональні. Цілі числа (integer) виражаються цифрами в десятковому записі. Раціональні числа можуть бути представлені в 3-х видах:

1. раціонального дробу з використанням оператора розподілу, наприклад: 28/70;

2. с плаваючою комою (float), наприклад: 2.3;

3. у показниковій формі, наприклад: 1,602*10^(-19) означає

1,60210^-19.

Для того, щоб одержати раціональне число не в точній формі, а у вигляді наближеного значення (числа із плаваючої коми), варто дописувати до цілої частини числа .0. Приклад:

> 75/4;

> 75/4.0;

18.75000000

В Maple можна записати букви грецького алфавіту в поліграфічному виді. Для цього в командному рядку набирається назва грецької букви. Наприклад, буква вийде, якщо набрати alpha.

Таблиця рядкових грецьких букв і їхніх назв:

	alpha			ita			sigma
	beta			kappa			upsilon
	gamma			lambda			phi
	delta			nu			chi
	epsilon			mu			psi
	zeta			xi			omega
	eta			pi
	theta			rho

Заголовні грецькі букви можна записати, якщо набирати назву грецької букви із великої літери, наприклад, щоб одержати , варто набрати Omega. Грецькі букви також можна набирати за допомогою спеціального меню.

Приклад 2.

1. Обчисліть значення . Для цього в командному рядку наберіть:

> (sqrt(6+2*sqrt(5))-sqrt(6-2*sqrt(5)))/sqrt(3);

і натисніть Enter. У результаті вийде точне значення .

2. Наберіть формули 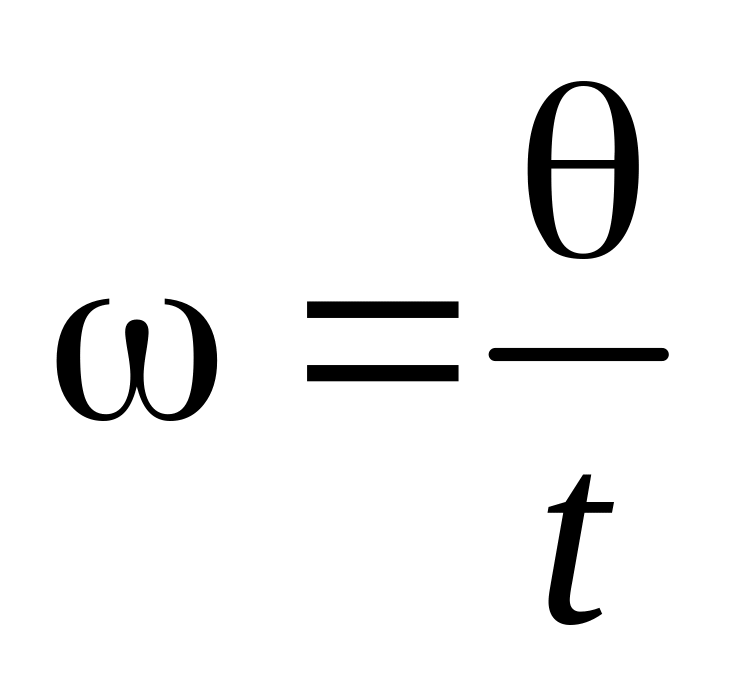й . Для цього в командному рядку наберіть:

> omega=theta/t; abs(f(x)+delta)<epsilon;

натисніть Enter.