2. Диференціювання
Обчислення похідних
Для обчислення похідних в Maple є дві команди:
прямого виконання – diff(f,x), де f – функція, яку треба продиференціювати, x – ім'я змінної, по якій здійснюється диференціювання.
відкладеного виконання – Diff(f,x), де параметри команди такі ж, як і в попередній. Дія цієї команди зводиться до аналітичного запису похідної у вигляді
.
Після виконання диференціювання,
отриманий вираз бажано спростити. Для
цього треба використовувати команди
simplify, factor
або expand,
залежно від того, у якому виді вам
потрібний результат.
Наприклад:
> Diff(sin(x^2),x)=diff(sin(x^2),x);
Для обчислення похідних старших порядків треба вказати в параметрах x$n, де n – порядок похідної; наприклад:
> Diff(cos(2*x)^2,x$4)=diff(cos(2*x)^2,x$4);
Отриманий вираз можна спростити двома способами:
> simplify(%);
> combine(%);
Диференціальний оператор
Для визначення диференціального оператора використовується команда D(f) – f-функція. Наприклад:
> D(sin);
cos
Обчислення похідної в точці:
> D(sin)(Pi):eval(%);
-1
Оператор диференціювання застосовується до функціональних операторів
> f:=x-> ln(x^2)+exp(3*x):
> D(f);
Приклад 2.
Обчислити похідну
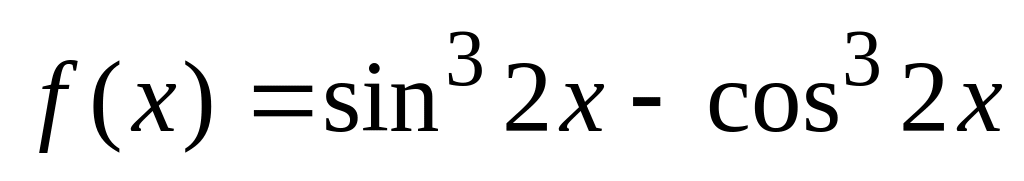
> Diff(sin(2*x)^3-cos(2*x)^3,x)=diff(sin(2*x)^3-cos(2*x)^3,x);
Обчислити
.
Наберіть:
> Diff(exp(x)*(x^2-1),x$24)=diff(exp(x)*(x^2-1),x$24):
> collect(%,exp(x));
Обчислити другу похідну функції
в точках
x=/2,
x=.
> y:=sin(x)^2/(2+sin(x)): d2:=diff(y,x$2):
> x:=Pi; d2y(x)=d2;
x:= d2y()=0
> x:=Pi/2;d2y(x)=d2;
х:=
3. Інтегрування
Аналітичне й чисельне інтегрування
Невизначений інтеграл
обчислюється за допомогою 2-х команд:
прямого виконання – int(f, x), де f – підінтегральна функція, x – змінна інтегрування;
відкладеного виконання – Int(f, x) – де параметри команди такі ж, як і в команді прямого виконання int. Команда Int видає на екран інтеграл в аналітичному виді математичної формули.
Для обчислення визначеного
інтегралу
до команд int
і Int
додаються границі інтегрування,
наприклад,
> Int((1+cos(x))^2, x=0..Pi)=int((1+cos(x))^2, x=0..Pi);
Якщо в команді інтегрування додати опцію continuous: int(f, x, continuous), то Maple буде ігнорувати будь-які можливі розриви підінтегральної функції в діапазоні інтегрування. Це дозволяє обчислювати невласні інтеграли від необмежених функцій. Невласні інтеграли з нескінченними границями інтегрування обчислюються, якщо в параметрах команди int вказувати, наприклад, x=0..+infinity.
Чисельне інтегрування виконується командою evalf(int(f, x=x1..x2), e), де e – точність обчислень (число знаків після коми).
Інтеграли, що залежать від параметру. Обмеження для параметрів
Якщо
потрібно обчислити інтеграл, що залежить
від параметру, то його значення може
залежати від знаку цього параметру або
яких-небудь інших обмежень. Розглянемо
як приклад інтеграл
,
що, як відомо з математичного аналізу,
сходиться при
а>0
і розходиться при а<0.
Якщо обчислити його відразу, то вийде:
> Int(exp(-a*x),x=0..+infinity)=int(exp(-a*x),x=0..+infinity);
Definite integration: Can't determine if the integral is convergent.
Need to know the sign of -і> a
Will now try indefinite integration and then take limits.
.
Таким способом інтеграл із параметром не обчислити. Для одержання явного аналітичного результату обчислень треба зробити які-небудь припущення про значення параметрів, тобто накласти на них обмеження. Це можна зробити за допомогою команди assume(expr1), де expr1 – нерівність. Додаткові обмеження вводяться за допомогою команди additionally(expr2), де expr2 – інша нерівність, що обмежує значення параметру з іншого боку.
Після накладення обмежень на параметр Maple додає до його ім'ені символ (~), наприклад параметр a, на який були накладені деякі обмеження, в строці виводу буде мати вигляд: a~.
Опис накладених обмежень параметру a можна викликати командою about(a). Приклад: накласти обмеження на параметр a такі, що a>-1, a3:
> assume(a>-1); additionally(a<=3);
> about(a);
Originally a, renamed a~:
is assumed to be: RealRange(Open(-1),3)
Повернемося до обчислення інтегралу з параметром , яке треба робити в такому порядку:
> assume(a>0);
> Int(exp(-a*x),x=0..+infinity)=int(exp(-a*x),x=0..+infinity);
Навчання основним методам інтегрування
В Maple є пакет student, призначений для навчання математиці. Він містить набір підпрограм, призначених для виконання розрахунків крок за кроком, так, щоб була зрозуміла послідовність дій, що приводять до результату. До таких команд належать інтегрування за частинами inparts і заміна змінної changevar.
Формула інтегрування вроздріб:
Якщо позначити підінтегральну функцію f=u(x)v’(x), то параметри команди інтегрування за частинами такі: intparts(Int(f, x), u), де u – саме та функція u(x), похідну від якої треба обчислити по формулі інтегрування за частинами.
Якщо в інтегралі потрібно зробити заміну змінних x=g(t) або t=h(x), то параметри команди заміни змінних такі: changevar(h(x)=t, Int(f, x), t), де t нова змінна.
Обидві команди intparts і changevar не обчислюють остаточно інтеграл, а лише роблять проміжне викладення. Для того, щоб одержати остаточну відповідь, треба, після виконання цих команд ввести команду value(%); де % - позначають попередній рядок.
Не забудьте, перед використанням описаних тут команд обов'язково завантажити пакет student командою with(student).
Приклад 3.
Знайти невизначені інтеграли: а)
;
б)
.
> Int(cos(x)*cos(2*x)*cos(3*x),x)=int(cos(x)*cos(2*x)*cos(3*x), x);
> Int((3*x^4+4)/(x^2*(x^2+1)^3),x)=int((3*x^4+4)/(x^2*(x^2+1)^3),x);
Знайти визначений інтеграл
,
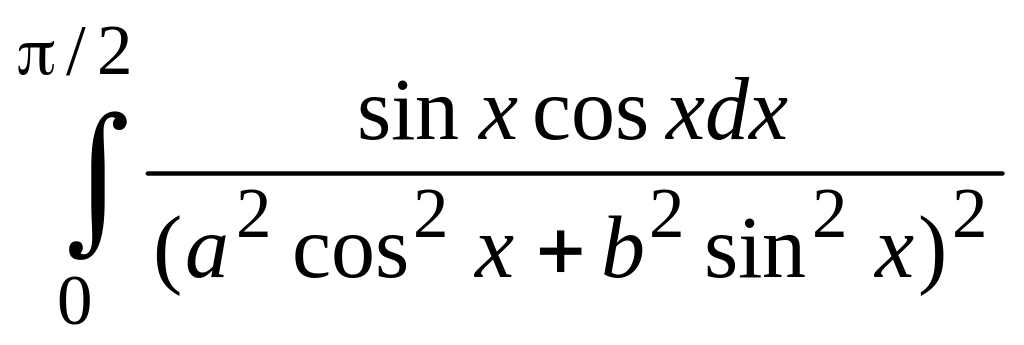за умови a>0,
b>0.
> assume (a>0); assume (b>0);
> Int(sin(x)*cos(x)/(a^2*cos(x)^2+b^2*sin(x)^2), x=0..Pi/2)= int(sin(x)*cos(x)/(a^2*cos(x)^2+ b^2*sin(x)^2), x=0..Pi/2);
Знайти невласний інтеграл
,
при a>-1
> restart; assume(a>-1);
> Int((1-exp(-a*x^2))/(x*exp(x^2)), x=0..+infinity)=int((1-exp(-a*x^2))/(x*exp(x^2)), x=0..+infinity);
Чисельно знайти інтеграл
> Int(cos(x)/x, x=Pi/6..Pi/4)=evalf(int(cos(x)/x, x=Pi/6..Pi/4), 15);
Повністю проробити всі етапи обчислення інтеграла
вроздріб.
> restart; with(student): J=Int(x^3*sin(x),x);
> J=intparts(Int(x^3*sin(x),x),x^3);
> intparts(%,x^2);
> intparts(%,x);
> value(%);
Обчислити інтеграл
за допомогою універсальної підстановки
.
> J=Int(1/(1+cos(x)), x=-Pi/2..Pi/2);
> J=changevar(tan(x/2)=t,Int(1/(1+cos(x)), x=-Pi/2..Pi/2), t);
> value(%);
J=2