4. Переходные процессы в цепях

с индуктивно связанными элементами

Известно, что число корней характеристического уравнения равняется числу независимых накопителей энергии в цепи. Влияет ли наличие индук-тивной связи элементов на число корней и, следовательно, на вид переход-ного процесса? Можно сразу сказать: не влияет, так как взаимная индуктивность М не создаёт нового элемента, она лишь изменяет индуктивности существующих элементов.

При последовательном соединении катушек это утверждение не вызыва-ет сомнений. Здесь хотя и имеется две катушки, но с точки зрения расчёта они могут быть заменены одним эквивалентным индуктивным элементом:

Lэкв = L₁+ L₂ ± 2M.

В случае разветвленной цепи и в трансформаторных схемах этот посыл доказывается применением развязки связи.

5. Переходные процессы при "некорректных коммутациях".

Законы коммутации в обобщённой форме.

В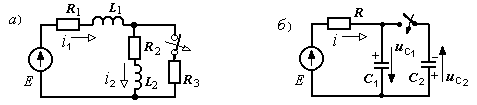 самом начале рассмотрения переходных процессов было принято допущение о том, что коммутация происходит мгновенно: tкомм = 0. На самом деле это не так, и в некоторых случаях, которые назовём "некорректными коммутациями", время коммутации приходится учитывать. Ниже приведе-ны два характерных случая процесса: в RL и в RC-цепи.

В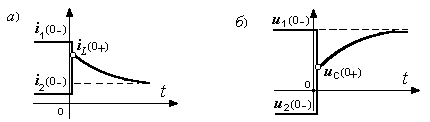 схеме “а” до коммутации ток i_1L (0-) больше тока i_2L (0-). В первый же момент после коммутации индуктивности соедине­ны последовательно, и эти токи должны быть одинаковыми. В схеме “б” первый конденсатор заря-жен до напряжения источника, второй конденсатор может быть не заряжен, или даже иметь обратную полярность напряжения, как показано на схеме. В первый же момент после коммутации напряжения на обоих конденсаторах должны быть одинаковыми.

На первый взгляд кажется, что в этих случаях наруша­ются законы ком-мутации. Это впечатление снимается, если учесть, пусть и очень малое, время коммутации от t = 0- до t = 0₊. Именно за это время происходит очень быст-рое выравнивание токов i в индуктивностях или напряжений u на конденсаторах, которое по отношению к плавной остальной части процесса воспринимается как скачкообразное. Значения тока i_L (0+) и напряжения u_С (0+) в этом случае рассчитывают исходя из общих принципов электрофизики - принципа непрерывности потокосцепления и принципа непрерывности заряда, которые и называют обобщёнными законами коммутации.

1. Суммарное потокосцепление системы, контура непрерывно, и в момент коммутации не может изменяться скачком:

Применительно к схеме “а” это означает, что потокосцепление контура из L₁ и L₂ в первый момент после коммутации будет равно алгебраической сумме потокосцеплений этих элементов непосредственно перед коммутацией:

.

Из этого выражения и находится значение тока i_L(0+). Соотношение спра-ведливо и в случаях, если до коммутации какая-то индуктивность не входила в контур, образовавшийся после коммутации, а также в случае индук-тивно связанных элементов. Знак же составляющих потокосцепления ψ(0-) принимается в зависимости от того, совпадает ли направление тока в эле-менте до коммутации с направлением тока после коммутации, или они яв-ляются встречными.

2. Суммарный заряд сходящихся в узле цепи ёмкостей непрерывен, и в момент коммутации не может изменяться скачком:

В этом случае суммарный заряд конденсаторов до коммутации также оп-ределяется алгебраически, с учётом направления токов заряда или напряжений на конденсаторах по отношению к рассматриваемому узлу цепи. Например, в схеме “б” заряд второго конденсатора должен быть принят со знаком минус. Величина напряжения u_C(0+) определяется из соотношения:

Об энергетической стороне процессов при некорректных коммутациях можно прочесть в учебнике: Атабеков Г.И. ТОЭ, 1978г, с.429 или Зевеке Г.В. ОТЦ, 1989г., стр.276.

------------- Скорректировано. АВХ, 1 ноября 2014г.------------------

Содержание стр.

ВВЕДЕНИЕ: определение, допущения, законы коммутации ……. 3

1. Основные положения классического метода расчёта ПП

- получение характеристического уравнения цепи ……… 6

- начальные условия процесса, постоянные интегрирования ……... 7

- рекомендуемая последовательность расчёта …………………….. 8

2. Переходные процессы в цепях с одним накопителем энергии:

- Включение RL-цепи на постоянное напряжение, tпп …………….. 8

- Включение RC-цепи на постоянное напряжение, tпп ………….... 11

- Особенности ПП в цепях синусоидального тока ……………..…. 11

Пример 1. ПП в цепи постоянного тока с индуктивностью … 12

Пример 2. ПП от серии прямоугольных импульсов

(квазиустановившийся режим) …………………… 14

Пример 3. ПП в цепи sin-тока с конденсатором ……………... 16

3.ПП в цепях с двумя разнородными накопителями энергии … 18

Пример 4. Расчёт апериодического процесса …………….. … 20

Пример 5. Расчёт предельного апериодического процесса … 21

Пример 6. Расчёт колебательного переходного процесса …... 23

4. ПП в цепях с индуктивно связанными элементами ………….. 25

5. Переходные процессы при некорректных коммутациях.

Законы коммутации в обобщённой форме …………………27-28.

-------------------------------------------- _*** ----------------------------------------------

Классический метод расчёта ПП.

Лекции. Типовые примеры расчёта.

Составитель – доц. Антамонов Валентин Харитонович

-------------------------------------------- _*** ----------------------------------------------

Литература

1. Атабеков Г.И. ТОЭ. Линейные электрические цепи. -М: Энергия, 1978г.

2. Основы теории цепей /Г.В.Зевеке, П.А.Ионкин, А.Нетушил, С.Страхов.

–М.: Энергоатомиздат, 1989г., стр.234-278.

3. Бессонов Л.А. ТОЭ. Электрические цепи. –М.: Высшая школа, 1978г.

4. Учебное пособие по решению задач по теоретической электротехнике.