3. Переходные процессы в цепях с двумя разнородными накопителями энергии

В цепях с двумя разнородными накопителями энергии, в зависимости от соотношения R,L,C-параметров, возможны апериодический и колебательный процессы. Иногда выделяют процесс на границе этих режимов, так называемый предельный апериодический процесс.

С физической точки зрения это объясняется тем, что, например, при разряде ёмкости часть энергии накапливается в индуктивном элементе. Если эта часть энер­гии мала, то она лишь затягивает процесс разряда, но если она доста­точно велика, то между индуктивностью и ёмкостью становится возможным обмен энергией, и в цепи возникает колебательный процесс.

Все эти виды ПП можно рассмотреть на примере простейшей цепи, в которой заряженный предварительно конденсатор разряжается на RL-нагрузку. Пример удобен и тем, что в схеме цепи нет источни­ков ЭДС, процесс заканчивается полным разрядом конденсатора. Ток и н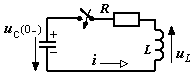 апряжения на эле­ментах в переходном процессе имеют только свободные составляющие. Обратим вни-мание на направление то­ка, которое, чтобы избежать путаницы со знаком в выражении iс = С∙duc /dt, всегда следует выбирать по направлению нап-ряжения на конденсаторе.

Итак, после замыкания рубильника цепь описывается одним уравнением по вто­рому закону Кирхгофа:

.

Для решения сводим его к чисто дифференциальному уравнению относи­тельно тока или относительно напряжения на конденсаторе:

.

Характеристическое уравнение цепи и его корни имеют вид:

;

Теперь уже математически очевидно, что в зависимости от соотношения R L C-параметров возможны три варианта корней характеристического уравнения и, следовательно, три вида процесса.

Случай А. Если соотношение параметров цепи будет таково, что

, или , или , то

корни уравнения будут вещественными, отрицательными, неравными. Сво-бодные составляющие токов и напряжений запишутся в виде суммы двух затухающих с разной интенсивностью экспонент:

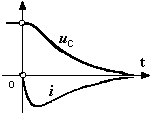
Процесс будет иметь аперио­дический характер /см. рисунок/. Но заметим, что апериодичес-кий процесс в цепи с двумя накопителями энергии отличается от подобного процесса в цепях с одним накопителем энергии. Здесь цепь характеризуется двумя постоянны­ми времени τ₁ , τ₂. Сначала она сравнительно быстро реагирует на воз­действие, а затем процесс протекает несколько спокойнее. Кривые u_C(t), i(t), u_L(t) представляют собой наложение двух экспонент, могут иметь точ-ки экстре­мума и точки перегиба. Длительность переходного процесса определяется большей постоянной времени: .

С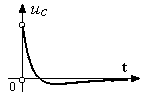 лучай Б. Если соотношение параметров таково, что , то кор-ни характеристического уравнения будут вещественные, отрица­тельные и равные: р₁= р₂ = р. Процесс в этом случае называют предельным апериоди-ческим, а свободные составляющие токов и напряжений записывают в виде:

Напряжение на конденсаторе в этом случае, убывая, переходит через значение iпр (t) = 0, но далее устанавливаются без совершения колебаний. По-этому такой режим и называют предельным апериодическим, а не «преде-льным» колебательным.

С лучай В. Если , то корни получаются комплексно-сопря-жёнными: . Свободные составляющие токов и напряжений в таком случае записывают в виде затухающих синусоиды и косинусоиды или в виде синусоиды с ненулевой начальной фазой, имеет мес­то колебательный процесс.

.

.

Колебательный процесс характеризуют частотой свободных колебаний ωсв и коэффициентом затухания этих колебаний δ, которые зависят и, со-ответственно, могут быть определены через соотношения параметров цепи непосредственно из корней характеристического уравнения:

; , рад/с.

Величины δ и ωсв можно определить и экспериментально, по осциллограммам – см. лабораторную работу по переходным процессам в RLC- цепи:

ωсв = , рад/с Δ = δ = , 1/с.

Величина, обратная коэффициенту затухания колебаний δ, соответству-ет постоянной времени τ цепи, через которую определяется длительность колебательного процесса: .

* Таким образом, для последовательного соединения RLC- элементов соотноше­ние параметров = Rкр является критическим. При та-ком соот­ношении происходит смена характера процесса в цепи.

О влиянии величины индуктивности или ёмкости на характер процессов, а также об энергетических соотношениях в цепи рекомендуем прочесть са-мостоятельно, например, в учебнике Зевеке Г.В, стр.246.

ПРИМЕРЫ РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В RLC-ЦЕПЯХ