1. Основные положения классического метода

РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

Н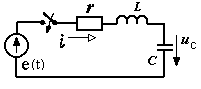 еразветвлённая RLС-цепь в переходном процессе описывается одним интегро-дифференциальным уравнением по II закону Кирхгофа

.

Для решения его сводят к чисто дифференци­альному уравнению вида:

В математике решение таких уравнений находится в виде суммы общего и частного решений. Частное решение зависит от вида правой части урав-нения, т.е. в данном случае от вида принуждающей ЭДС. Общее решение - это решение уравнения при нулевой правой части, т.е. при отсутствии в це-пи источников. Поэтому в электротехнике их называют принуждённой и свободной составляющими тока или напряжения ПП.

.

Принуждённые составляющие токов и напряжений i_пр (t), u_пр (t) рассчи-тываются по схе­ме цепи в установившемся после коммутации режиме. Это обычный расчёт цепи постоянного или переменного тока.

Расчёт составляющих i_св (t), u_св (t) выполняется в следующем порядке:

- для цепи после коммутации в свободном режиме (источники исключены) составляется характеристическое уравнение и находятся его корни;

- по виду корней записывается общий вид свободных составляю­щих;

- в выражениях свободных составляющих рассчитываются постоянные интегрирования.

После этого, как сумма составляющих, записывается полное решение:

i (t) = i пр(t) + i св(t) ; u (t) = u пр(t) + u св(t)

* Способы получения характеристического уравнения цепи

Если цепь содержит несколько накопителей энергии, то характеристическое уравнение цепи получают следующим образом: для цепи после коммутации в свободном режиме по МЗК составляются диф-ференциальные уравнения, которые затем алгебраизируются путём замены d /dt → p, . Приравнивая главный определитель систе­мы к нулю, получают искомое характеристическое уравнение цепи:

,

Если же цепь достаточно простая, то характеристическое уравнение получают через запись входного операторного сопротивления це-пи Zвх(р) = 0 в свободном режиме, причём, относительно любой ветви.

Пример.

R = 10 Ом, L = 18,4 мГн, С = 500 мкФ.

Найти Zвх(р) и записать характеристичес-кое уравнение цепи в переходном процессе.

Выражение получается проще, если входное сопротивление записывать относительно ветви с накопителем энергии.

= = 0,

р² + 200р + 108695.65 = 0 = -100 ± j314 1/c.

* Корни уравнения, их свойства и вид свободных составляющих.

Число корней и порядок характеристического уравнения определяют­ся числом независимых накопителей энергии в цепи. Поскольку цепь линейная, переходный процесс в ней всегда затуха­ет, поэтому корни характеристического уравнения отрицательны или имеют отрицательную веществен-ную часть. Свободные составляющие то­ков и напряжений записывают в ви-де затухающих экспонент:

;

.

Выражения свободных составляющих, как видим, содержат постоянные интегрирования, которые предстоит определить. Их находят через начальные значения функций и их производных, т.е. в нашем понимании, через начальные условия переходного процесса iq(0+), uq(0+), i' (0+), u'(0+).

* Начальные условия процесса.

* Расчёт постоянных интегрирования.

В электротехнике различают докоммутационные /t = 0-/ и послеком-мутационные / t = 0₊/, нулевые и не­нулевые, зависимые и независимые на-чальные условия. К независимым начальным условиям относят­ся значения тока в индуктивности i_L(0) и напряжения на ёмкости u_C(0), посколь-ку в момент коммутации они не могут измениться скачком. Их рассчитывают по схеме цепи ещё до коммутации: i_L (0₊) = i_L(0_-), u_C (0₊) = u_C(0-).

Значения остальных токов и напряжений являются зависимыми начальны­ми условиями. Их рассчитывают в момент t = 0+, т.е. в первый же момент после коммутации, рассчитывают по МЗК или любому иному методу. После этого постоянные интегрирования находят из выражений свободной составляющей, рассмотренной при t = 0+:

при одном корне А = i (0+) - iпр (0+) ;

при двух корнях А₁ + А₂ = i (0+) – iпр (0+) ;

р₁А₁ + р₂А₂ = i' (0+) – i’пр (0+) .

Рекомендуемый порядок расчёта переходного процесса

классическим методом

1. До коммутации рассчитываются независимые начальные условия процесса: i_L(0-), u_C(0-).

2. После коммутации в установившемся режиме цепи рассчитываются при­нуждённые составляющие токов и напряжений i пр(t), uпр(t).

3. В свободном режиме цепи после коммутации получают характеристическое уравнение цепи, находят его корни, по виду которых записывают общий вид свободных составляющих iсв(t), uсв(t).

4. Для определения постоянных интегрирования рассчитывают на­чальные значения величин i (0₊), u (0₊) и их производных: i^′(0₊), u^’(0₊). Расчёт цепи в момент времени t = 0₊ обычно выполняют по МЗК.

Через полученные начальные значения величин и определяют постоянные интегрирования в выражениях свободных составляющих.

5. Полные выражения токов и напряжений в переход­ном процессе записывают в виде суммы: u (t) = uпр(t) + uсв(t), i (t) = i пр (t) + iсв(t).