4.2.2. Кривые безразличия и их свойства

Графически система предпочтений потребителя изображает­ся с помощью кривых безразличия (впервые применены англий­ским экономистом Ф. Эджуортом в 1881 г.).

Кривая безразличия — геометрическое место точек, каждая из которых представляет такую комбинацию двух видов товаров (х и у), что потребителю безразлично, какую ему выбрать. Другими словами, кривая безразличия показывает альтернативные наборы товаров, обеспечивающие оди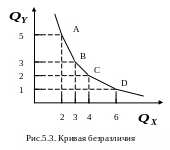 наковый уровень полезности (рис. 4.3).

Н а представленной кривой безразличия выделены четыре равнополезные комбинации двух видов благ в точках А, В, С, D.

Эти комбинации дают потребителю одинаковое общее удовлетворение, то есть

Набор кривых безразличия для одного потребителя и одной пары благ образует карту безразличия (рис. 5.4).

Свойства кривых безразличия вытекают из аксиом, на которых базируется порядковый подход:

1. Наборы, представленные кривыми безразличия, более удаленными от начала координат, обеспечивают потребителю большую полезность, а потому – предпочтительнее, чем наборы на менее удаленных кривых. Это вытекает из предположения, что большее количество благ предпочитается меньшему. На рис. 5.4.

2. Касательная, проведенная к любой точке кривой безразличия, имеет отрицательный угол наклона.

Пусть точка А (рис. 5.5.) представляет определенный набор товаров X и Y. Проведем через нее две взаимно перпен­дикулярные прямые.

Все точки, лежащие в III квадранте, представляют большие, а все точки, лежащие в I квадранте — меньшие количества товаров X и Y, чем точка А. В соответствии с аксиомой ненасыщения наборы, представленные в III квадранте, предпочтительнее, а наборы в I квадранте — менее предпочтительны, чем набор А. Значит, наборы, эквивалентные А, должны быть представлены точками, находящимися во II и IV квадрантах (В,D). Следовательно, кривая безразличия имеет отрицательный наклон.

3 . Кривые безразличия не пересекаются.

Представим обратное. Предположим, что две кривые безразличия пересекаются в точке А (рис. 5.6).

Наборы А и B находятся на одной кривой . Значит они эквивалентны. То же самое можно сказать о наборах А и С, которые расположены на одной кривой . Если B ~ A ~ C, то B ~ C. Но набор С соответствует большему количеству X и Y. Отсюда следует, что . Поскольку потребитель не может одновременно предпочитать С перед В и не делать различия между ними, пересечение двух кривых означает противоречие.

5.2.3 Предельная норма замены и конфигурация кривой безразличия

Конфигурация кривой безразличия определяется предельной нормой замещения (предельной нормой замены, предельной нормой субституции).

Предельной нормой замены благом X блага Y называется количество блага Y, которым потребитель должен пожертвовать ради увеличения потребления блага X на одну единицу при неизменном уровне общего удовлетворения потребителя (рис. 5.7).

П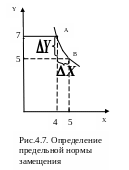 ереходя от набора А к набору В потребитель сокращает потребление товара Y на ед. в обмен на увеличение товара X на ед., но общий уровень удовлетворения потребителя при этом остается неизменным.

Тогда предельную норму замены благом X блага Y можно определить по формуле:

Если перейти к бесконечно малым изменениям (максимально приблизить точку В к точке А), то в этом случае MRS равна угловому коэффициенту наклона касательной к кривой безразличия в точке А.

Знак минус означает, что изменения количества двух благ происходят в противоположных направлениях, то есть положительному из­менению одного блага соответствует отрицательное изменение другого. Это является дополнительным доказательством того, что касательная, проведенная к любой точке кривой безразли­чия, имеет отрицательный угол наклона.

Если потребитель при выборе другого набора желает остать­ся на той же кривой безразличия, то прирост полезности от добавленного должен быть равен потере полезности от изъятого , то есть:

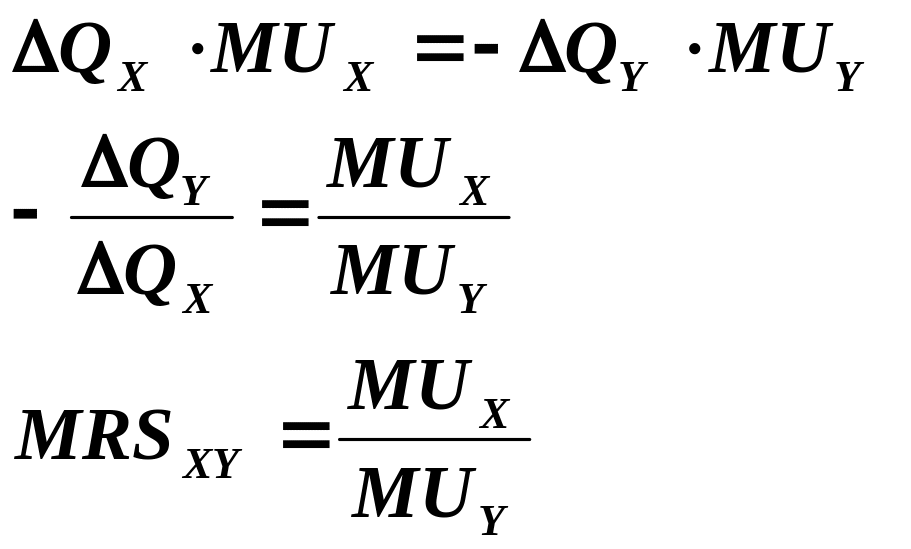
Значит, предельная норма замены благом X блага Y может

рассматриваться как соотношение предельных полезностей этих благ.

Поскольку уменьшается по мере замены товаром X товара Y, a , соответственно, увеличивается, отношение , равное , уменьшается. Это проявляется на графике в убывании углового коэффициента наклона касательной по мере движения вниз вдоль кривой безразличия и объясняет ее вогнутый характер.

Умень­шающаяся предельная норма замены в порядковой теории имеет тот же смысл, что и убывающая предельная полезность в ко­личественной теории. Только во втором случае полезность каждой дополнительной единицы товара оценивается в ютилах, а в первом — объемом другого товара, от которого потреби­тель готов отказаться.

Вогнутый характер кривых безразличия — наиболее общая и распространенная ситуация. Однако условие уменьшающейся предельной нормы замены не всегда соблюдается (см. рис. 5.8, 5.9, 5.10, 5.11).

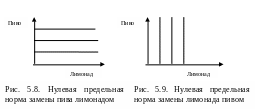Нулевая предельная норма замены характерна для тех случаев, когда потребитель не поступится даже бесконечно малым количеством товара в пользу другого (рис.5.8 и 5.9).

Предельная норма замены также равна нулю для товаров, жестко дополняющих друг друга (рис. 4.10).

В этом случае кривые безразличия имеют L-образный вид (вид прямых углов).

Д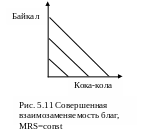 ля двух совершенно взаимозаменяемых товаров MRS — постоянная величина (рис.5.11).

В данной ситуации потребителю все равно, выпить ли стакан кока-колы или напитка «Байкал», поскольку оба товара воспринимаются им как один. Тогда кривые безразличия представляют собой прямые линии, имеющие отри­цательный наклон.