Линейно-зависимые и линейно независимые системы векторов.

Система векторов называется линейно-зависимой, если можно подобрать такие числа , , . . . , не все равные нулю ( есть ≠0), что

( - нуль-вектор)

Система векторов называется линейно-независимой, если из данных векторов нельзя составить нулевую линейную комбинацию с отличными от нуля коэффициентами, т.е. для линейно-независимой системы векторов выражение (1.3) справедливо тогда, когда все коэффициенты =0, .

Справедливы следующие утверждения.

Лемма. Если часть системы векторов линейно-зависима, то и вся система векторов линейно-зависима.

Теорема 1. Если система векторов линейно-зависима, то хотя бы один из них можно представить в виде линейной комбинации остальных векторов.

Следствие 1. Если хотя бы один вектор системы линейно выражается через остальные векторы, то система линейно-зависима.

Следствие 2. В линейно-независимой системе ни один из векторов нельзя выразить через остальные.

Теорема 2: Если каждый из векторов системы линейно выражается через векторы (k<m), то система векторов линейно зависима.

Теорема 3: В n-мерном пространстве любая система, содержащая более чем n векторов линейно - зависима.

Следствие: В n-мерном пространстве любая линейно – зависимая система может содержать не более n векторов.

Таким образом, на плоскости линейно – независимыми могут быть только два вектора. Любой третий вектор можно представить линейной комбинацией этих двух векторов. В 3-х мерном пространстве линейно - независимыми могут быть не более трёх векторов и т.д.

Начало формы

Пример : Является ли система векторов = (1;0;0); = (0;1;0) и = (0;0;1) линейно зависимой?

Решение: Составляем нулевую линейную комбинацию:

(1;0;0)λ₁ + (0;1;0)λ₂ + (0;0;1)λ₃ =(0;0;0)

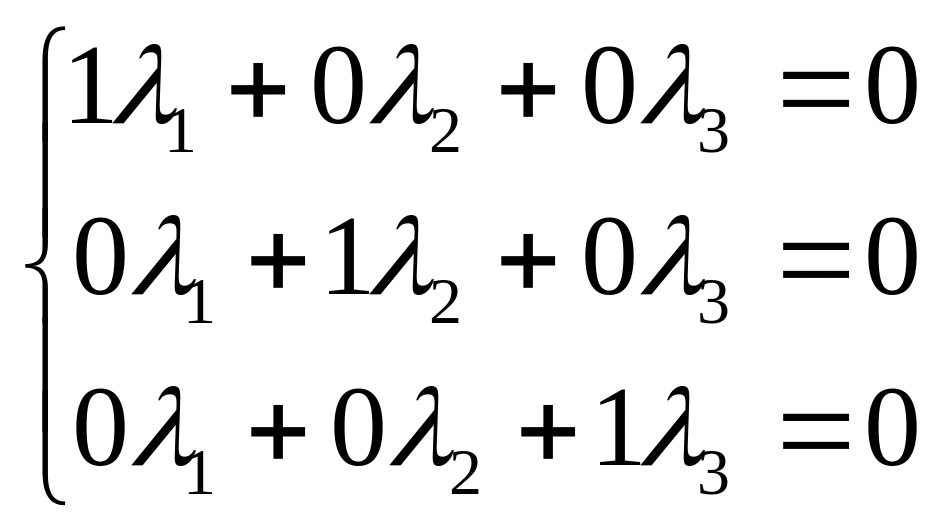или

Все значения , следовательно, система векторов – линейно – независима. Очевидно, что система из n n-мерных ортов является линейно-независимой.

Ранг и базис системы векторов

Наибольшее число r линейно-независимых векторов данной системы (n-мерного пространства) называется рангом данной системы векторов (n-мерного пространства).

Базисом системы векторов, имеющей ранг r, называется любая группа из r линейно-независимых векторов данной системы.

Базисом n-мерного пространства является любая система из n линейно-независимых векторов. Базисов в n-мерном пространстве бесчисленное множество, один из них система из n n-мерных ортов:

Такой базис называется единичным.

Теорема: Если набор линейно-независимых векторов является базисом некоторого множества векторов, то любой вектор этого множества можно представить линейной комбинацией базисных векторов:

Такое представление называется разложением вектора по базису , коэффициенты разложения определяются для данного вектора однозначно.

Пример : Дана система векторов и

Показать, что векторы образуют базис трехмерного пространства и найти разложение вектора в этом базисе.

Найдем решение системы уравнений:

(-1; 2; 0)λ₁+(3; 1; -1)λ₂+(4; 0; 2)λ₃=(-3; 5; -3).

Решив систему получили единственное решение системы уравнений: , подставляя в которое получаем разложение вектора по базису, который образуют векторы :

20