2. Действия над матрицами.

1) Сложение матриц и умножение матриц на число.

Складывать можно только матрицы одинакового порядка ( с одинаковым числом строк и столбцов).

Суммой матриц и называется матрица , элементы которой равны суммам соответствующих элементов матриц и .

, .

Пример: .

Чтобы умножить матрицу на число , нужно каждый элемент матрицы умножить на .

Пример: , . .

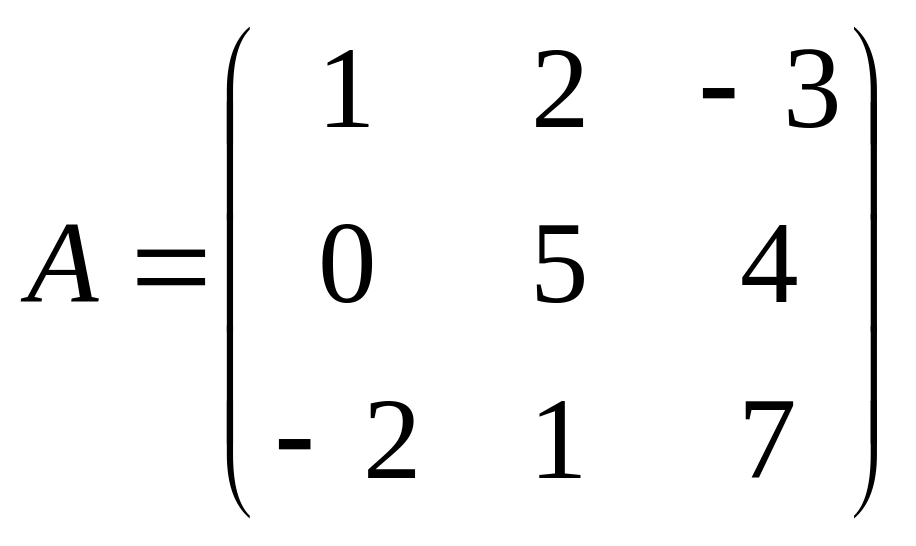Матрица называется противоположной матрице и обозначается .

Свойства умножения матрицы на число и сложения матриц

( – матрицы, – числа)

1. 5.

2. 6.

3. 7.

4. 8.

2) Умножение матриц.

Произведение матриц на определено только в том случае, когда число столбцов матрицы равно числу строк матрицы . В результате умножения получается матрица , у которой столько же строк, сколько их в матрице , и столько же столбцов сколько их в матрице .

Элемент матрицы , стоящий в -й строке и -м столбце равен сумме произведений элементов -й строки матрицы на соответственные элементы -го столбца матрицы . Поэтому правило умножения матриц часто называют правило умножения «строки на столбец».

; .

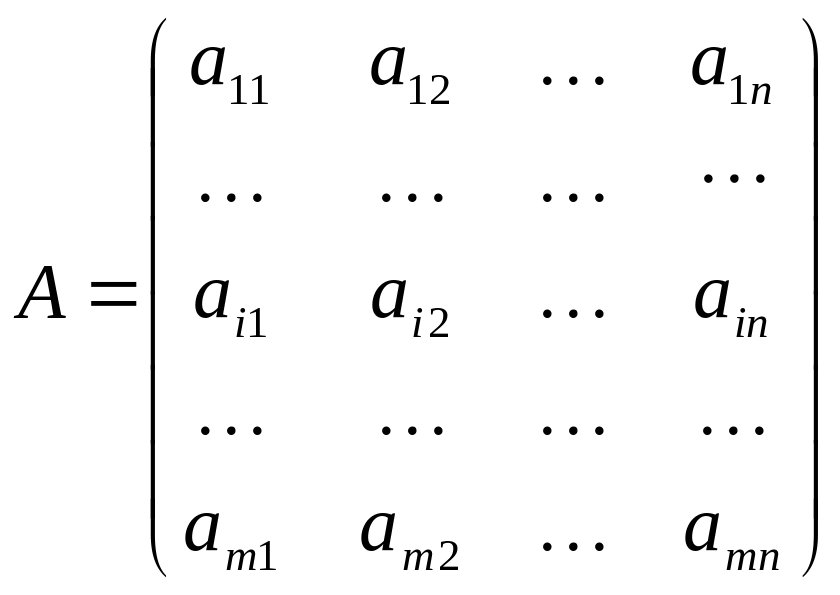Обозначим элементы через . Тогда .

Свойства умножения матриц

1.

2.

3.

4.

5. . Матрицы, для которых выполняется равенство , называются перестановочными.

6. , где – единичная матрица. Т. об., матрица при умножении матриц играет такую же роль, что и число 1 при умножении чисел.

7.

8. произведение матриц может оказаться нулевой матрицей, хотя оба сомножителя не являются нулевыми матрицами.

; ; .

Транспонированная и обратная матрица.

Пусть даны матрицы 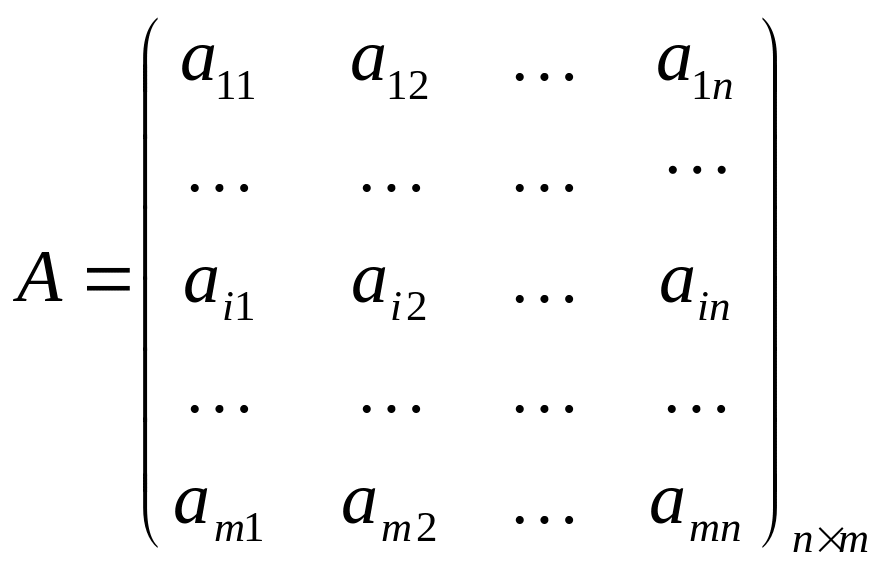и ,

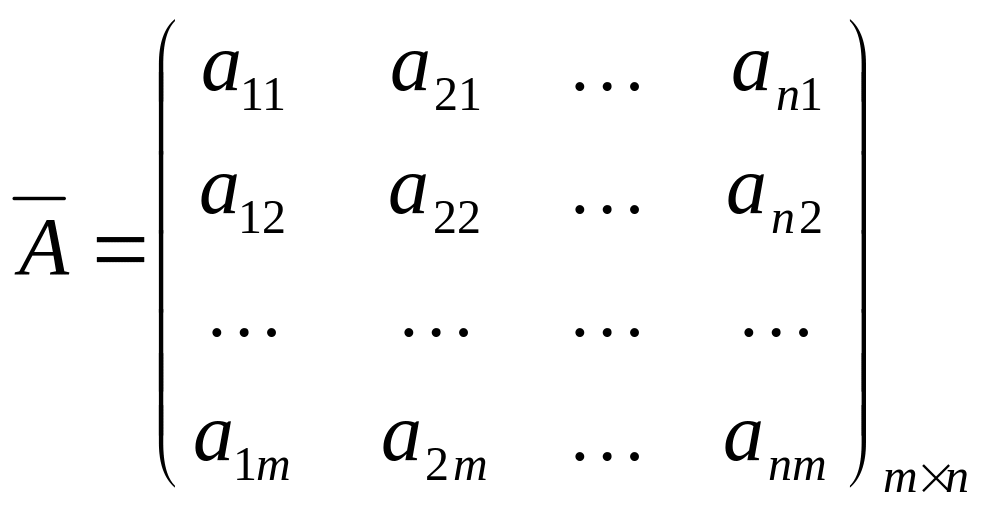которую получают из матрицы , заменяя строки на столбцы, а столбцы на строки, называется транспонированной матрицей по отношению к матрице .

Если размер матрицы , то размер матрицы

Повторное транспонирование приводит к исходной матрице.

Свойства транспонирования

1.

2.

3.

Рассмотрим квадратную матрицу .

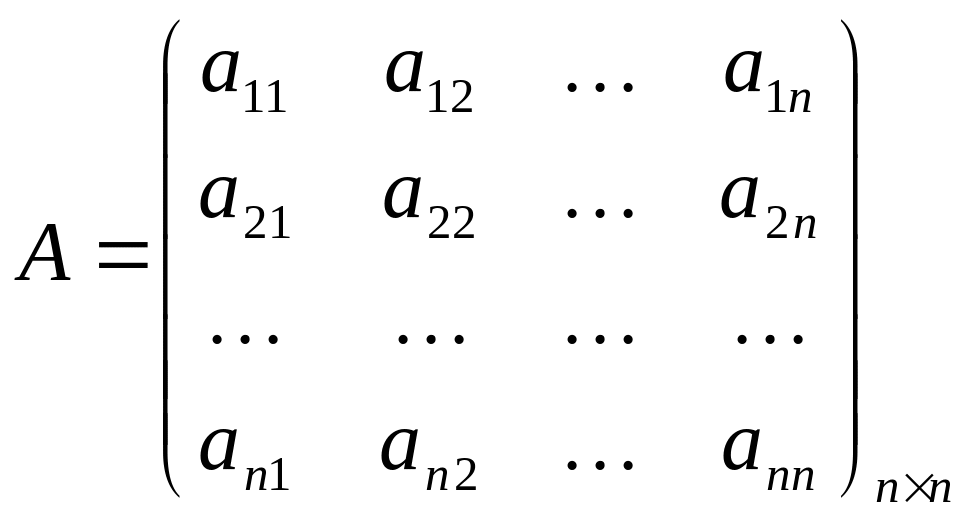Эта матрица называется обратимой, если можно подобрать такую матрицу , что .

Здесь матрица называется обратной квадратной матрице . Для каждой матрицы существует лишь одна обратная матрица. Если для матрицы существует обратная матрица, то ее будем обозначать . Итак, квадратная матрица обратима, если она имеет матрицу , такую что .

Не каждая квадратная матрица имеет обратную. Например, нулевая матрица не имеет обратной матрицы .

Квадратная матрица называется вырожденной, если ее определитель равен нулю и невырожденной в противном случае.

Квадратная матрица обратима тогда и только тогда, когда она невырождена.

Пусть дана матрица . Вычислим определитель матрицы

.

Если , то матрица имеет обратную матрицу, которая вычисляется по формуле:

,

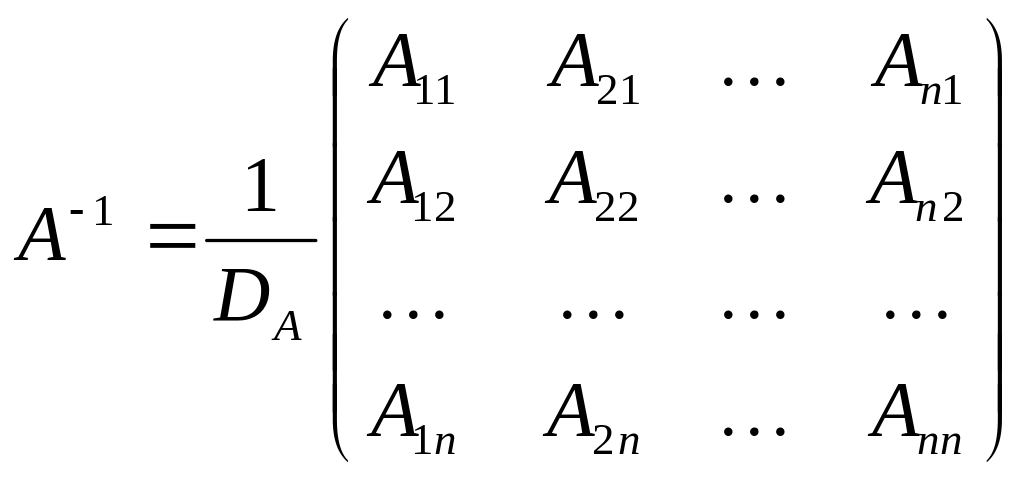Где – алгебраические дополнения определителя .

Свойства, связанные с обратной матрицей

1) ; 2) ; 3) .