Определители второго и третьего порядка, их вычисление и свойства.
1. Определители второго порядка.
Определение:
Системой линейных уравнений относительно
неизвестных
называется конечная совокупность
уравнений вида:
Где
–действительные числа,
– коэффициент при неизвестной
;
–
свободный член в
-
м уравнении.
Определение:
Решением системы уравнений называется
упорядоченная совокупность
чисел
,
которая является решением каждого
уравнения системы.
Любую линейную систему уравнений, в которой число строк совпадает с числом столбцов, можно решить, используя понятие определителя.
Определение: Определителем (детерминантом) II порядка называется выражение вида
.
Числа
называются элементами определителя.
Они расположены в двух строках и двух
столбцах, называемых рядами определителя.
Из определения определителя вытекает правило «развертывания » определителя II – го порядка, а именно: определитель II – го порядка равен разности произведений его элементов первой (главной) и второй диагонали.
Пример: Вычислить определитель:
2. Определители третьего порядка.
Определение:
Выражение вида
называется определителем III-го
порядка. Элементы определителя расположены
в трех строках и трех столбцах (ряды
определителя). Вычислять определитель
III-го
порядка можно несколькими способами:
1) правило Саррюса ( правило треугольника):
.
Из этой формулы следует правило вычисления определителя третьего порядка, которое называется правилом «треугольника». Вычислять определитель можно по схеме:
+ –
Пример: Вычислить определитель:
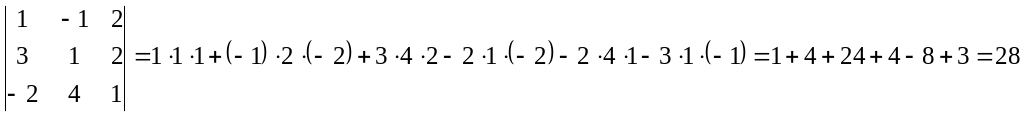
2) правило приписывания строк:
3) правило приписывания столбцов.
Определение: Под минором элемента определителя III-го порядка понимается определитель младшего (II-го) порядка, получающийся из данного определителя, в результате вычеркивания строки и столбца, содержащих данный элемент.
Минор обозначают
,
где
-
номер строки,
-
номер столбца.
Пример: Для предыдущего определителя найдем миноры
;
.
В дальнейшем будем говорить, что элемент определителя занимает четное место, если сумма номеров его строки и столбца есть число четное и нечетное, если такая сумма есть число нечетное.
Знаки элементов определителя, приписываемые минорам, можно задать таблично:
+ |
– |
+ |
– |
+ |
– |
+ |
– |
+ |
Определение: Алгебраическим дополнением (минором со знаком) элемента определителя III-го порядка называется минор этого элемента, взятый со знаком «+», если элемент занимает четное место и со знаком «–» – если его место нечетное.
Алгебраические дополнения вычисляются по формуле:
.
Пример:
.
Теорема разложения определителя III-го порядка: Определитель III-го порядка равен сумме парных произведений элементов какого – либо ряда его на их соответствующие алгебраические дополнения ( под рядом понимают строку или столбец).
Т. об., для определителя III-го порядка справедливы 6 разложений :
а) по трем строкам: б) по трем строкам:
.
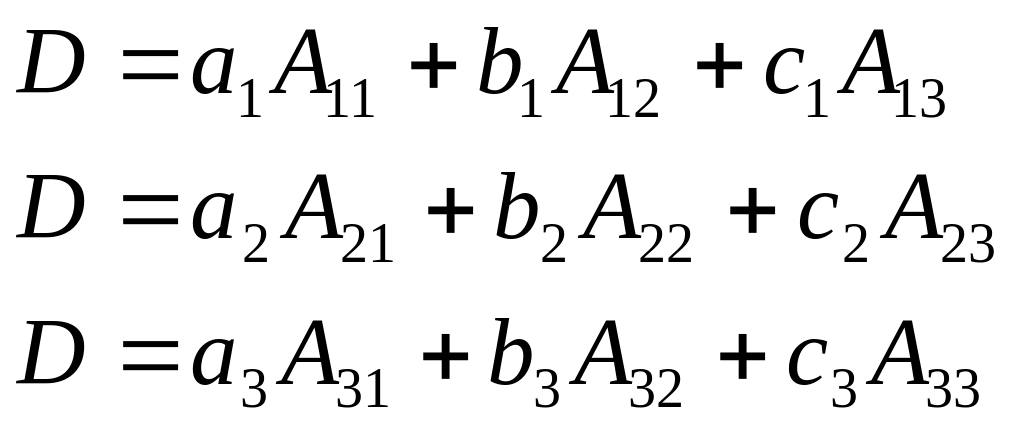
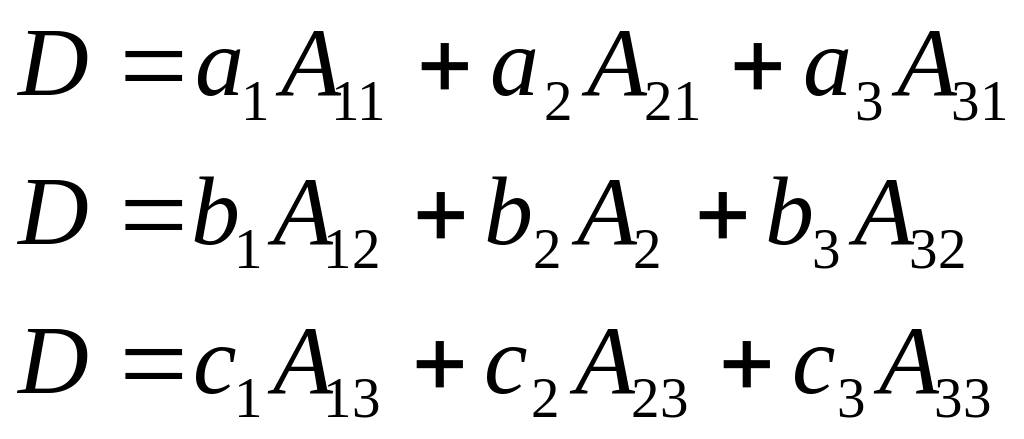Пример: вычислить определитель, разложив его по элементам того ряда, который содержит наибольшее число нулей
.