Радиотехнические системы передачи информации

4. Элементы теории линейного разделения каналов

4.1. Функциональная схема многоканальной спи

Современные системы передачи информации (радиотелеграфия, радиоуправление, телефония, телеграфия и т.д.) обеспечивающие передачу информации от сотен источников строятся по следующей схеме

Рис. 4.1

Операции кодирования и декодирования сообщений исключены, т.к. не являются обязательными.

Канальные сообщения 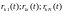поступающие от N независимых источников, с помощью канальных передатчиков преобразуются в канальные сигналы (модулированные поднесущие).

Преобразование представляется некоторым оператором , так что

Все N канальных сигналов складываются, и в результате получаем сложное колебание

- линейное (линия связи) многоканальное сообщение (групповой сигнал).

В общем передатчике это колебание вновь преобразуется в сигнал, но теперь уже высокочастотный. Преобразование отражается оператором М, в результате образуется сигнал

,

который излучается в пространство.

Общий передатчик, среда и общий приемник образует линию связи многоканальной системы, которая не отличается от одноканальной по своей структуре.

На вход приемника воздействует колебание

,

где h(t)-колебание обусловленное действием аддитивных помех и искажений,

k(t) –коэффициент, учитывающий действие мультипликативных помех и искажений.

Работа приемника характеризуется оператором , обратным оператору М. Без учета мультипликативных помех

- продукты помех и искажений на выходе приемника.

Действие каждого канального демодулятора характеризуется некоторым оператором P_l который, действуя на колебание выделяется на выходе l-го канала сигнал , а все остальные сигналы задерживаются, т.е. при отсутствии помех и искажений

,

то есть селектор l канала окликается лишь на сигналы .

В канальных приемниках происходит обратное преобразование канальных сигналов в сообщения при помощи оператора

.

Существуют линейные и нелинейные способы разделения каналов. Система линейна, если разделение каналов происходит в линейных селекторах (фильтрах) с постоянными или переменными параметрами, в противоположном случае – система нелинейна.

Теория разделения каналов должна отвечать на следующие вопросы:

1. Каким требованиям должны удовлетворять канальные сигналы, чтобы обеспечить их наилучшее разделение и по каким параметрам сигналов такое разделение можно осуществить?

2. Какова структура приемного устройства, при которой обеспечивается минимум взаимных помех между каналами, если, параметры канальных сигналов известны точно?

Эти вопросы могут решаться с учетом действия помех.

Основы линейного разделения сигналов заложил в 1935 г. наш соотечественник Д.В. Агеев, «Основы теории линейной селекции».

4.2. Геометрическое представление сигналов

Сигнал может быть представлен наглядно на основе геометрической интерпретации. Запишем его в виде ряда Котельникова (некоторая разновидность ряда Фурье).

Ряд Котельникова отличается тем, что его коэффициенты разложения представляют собой эффективные (а не амплитудные) значения гармоник ряда. Кроме того, в нем учитывается конечное число компонент спектра, т.к. любой радиоприемник обладает конечной полосой пропускания.

Итак, ряд Фурье имеет вид

Ряд Котельникова:

.

Не трудно показать, что

Верхняя и нижняя частоты спектра

Число гармоник . Коэффициент 2 перед скобкой, т.к. каждой частоте соответствуют синусная и косинусная составляющие

.

Сигнал с длительностью и спектром характеризуется независимыми значениями.

Если обозначить

то ряд Котельникова можно выразить в виде

Полученное выражение можно рассматривать как радиус-вектор в многомерном пространстве.

Из векторной алгебры известно, что (рис. 4.2)

,

Рис. 4.2

где , , - проекции вектора А на оси ОХ, ОУ, ОZ (скаляры вектора А),

i, j, k – орты (единичные векторы, определяющие направления).

Из определения скалярного произведения двух векторов

следует, что скалярное произведение ортов друг на друга равно нулю, а орта самого на себя равно единице

Скалярное произведение двух функций A(t) и B(t) есть среднее значение их произведения в интервале времени [-T/2; T/2], т.е.

Если произведение А(t) B(t) = 0, то функции А(t) и B(t) называются ортогональными.

Сигнал S(t) можно представить некоторым радиус-вектором m-мерного пространства или точкой, соответствующей концу этого вектора.

Проекции радиус-вектора на координатные оси определяются значениями коэффициентов C_k. Число таких проекций m = 2 . Т.к. сигналы являются функциями времени, то соответствующие им векторы в многомерных пространствах (их концы) описывают линии, называемые линиями сигналов.

Скалярное произведение сигнала самого на себя есть средняя мощность сигнала, которую он развивает на сопротивлении в 1 ом

.

Эффективное значение

Средняя удельная энергия сигнала

Если для ряда сигналов

выполняется условие

то такие сигналы называются ортогональными.