41.Ферромагнетизм. Свойства ферромагнетиков. Объяснение природы.

Возникновение магнитных свойств у ферромагнетиков связано с их доменным строением. Домены - это области самопроизвольной намагниченности, возникающие даже в отсутствие внешнего магнитного поля, в которых магнитные моменты атомов ориентированы параллельно.

Атомы или ионы приобретают магнитный момент, как правило, если они имеют нескомпенсированные спины электронов. Например в атомах железа на внутренней 3d-оболочке имеется четыре нескомпенсированных спина. Так как самопроизвольная намагниченность относится к внутриатомным явлениям, то ее природа может быть установлена только на основе квантово-механических понятий.

По Я.И.Френкелю и В.Гейзенбергу главную роль в возникновении ферромагнитного состояния играют силы обменного взаимодействия между атомами, имеющие квантовый характер и по происхождению являющиеся электростатическими.

Природа ферромагнетизма. Ферромагнетизм объясняется магнитными свойствами электронов. Электрон эквивалентен круговому току или вращающемуся заряженному телу и поэтому обладает собственным магнитным полем. В большинстве кристаллов магнитные поля электронов взаимно компенсируются благодаря попарной антипараллельной ориентации магнитных полей электронов. Лишь в некоторых кристаллах, например в кристаллах железа, возникают условия для параллельной ориентации собственных магнитных полей электронов. В результате этого внутри кристалла ферромагнетика возникают намагниченные области протяженностью 10^-2 - 10^-4 см. Эти самопроизвольно намагниченные области называются доменами (рис. 191, а).

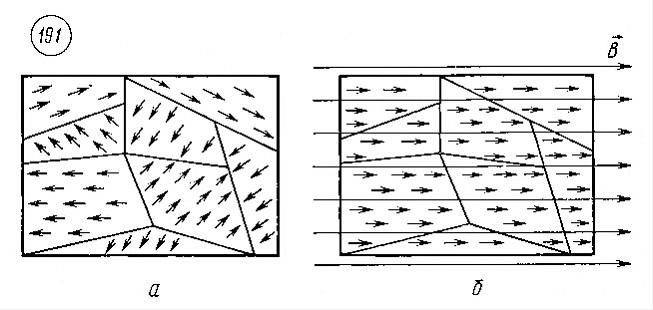
В отдельных доменах магнитные поля имеют различные направления и в большом кристалле взаимно компенсируют друг друга. При внесении ферромагнитного образца во внешнее магнитное поле происходит упорядочение ориентации магнитных полей отдельных доменов. С увеличением магнитной индукции  внешнего поля возрастает степень упорядоченности ориентации отдельных доменов — магнитная индукция  возрастает. При некотором значении индукции внешнего поля наступает полное упорядочение ориентации доменов (рис. 191, б), возрастание магнитной индукции прекращается. Это явление называетсямагнитным насыщением.

ФЕРРОМАГНЕТИЗМ - магнитоупорядоченное состояние вещества, в к-ром большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной (спонтанной) намагниченностью. Ф. устанавливается при темп-ре Т ниже Кюри точки Т_C в отсутствие внеш. магн. поля Н. В более широком смысле Ф. наз. совокупность физ. свойств вещества в указанном состоянии. Вещества, в к-рых возникает ферро-магн. упорядочение магн. моментов (рис. 1), наз. ферромагнетиками ,к их числу относятся как твёрдые кри-сталлич. вещества (см., напр., Магнитные диэлектрики, Магнитные полупроводники, Редкоземельные магнетики), так и нек-рые аморфные магнетики и металлические стёкла, а также магнитные жидкости .Ответственным за Ф. является обменное взаимодействие в м а г н е т и з м е, стремящееся установить спины (а следовательно, и магн. моменты) соседних атомов или ионов параллельно друг другу; в этом случае обменный интеграл имеет положит. значение.

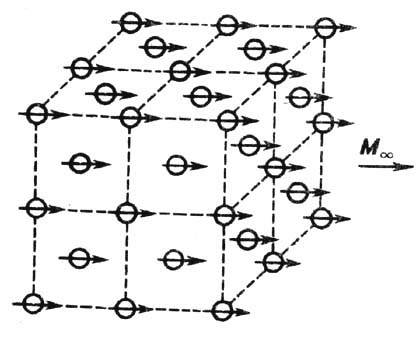
Рис. 1. Ферромагнитная коллинеарная атомная структура в гранецентрированной кубической решётке ниже точки Кюри Т_C;стрелками обозначены направления атомных магнитных моментов.

Ф. обычно наблюдается в трёхмерных системах, однако возможно его возникновение и в реальных квазиодномерных и квазидвумерных системах (см., напр., Слоистые магнетики)без нарушения Мёрмина-Вагнера теоремы. Ферромагн. атомный порядок можно непосредственно наблюдать методом магнитной нейтронографии, к-рый позволяет также определить величины атомных магн. моментов в узлах кристаллич. решёток разл. типов и пространственное распределение плотности магн. момента вблизи них. Кроме нейтронов аналогичную информацию (в т. ч. о внутр. полях на ядрах) могут дать ядерный магнитный резонанс, а также мюонной спиновой релаксации метод и мёссбауэровская спектроскопия.

Магнитная восприимчивость ферромагнетиков может достигать значений 10⁴-10⁵ Гс/Э; их намагниченность М, возникающая во внеш. магн. поле H, растёт с его величиной нелинейно (см. Намагничивание)и в полях   может достигать магнитного насыщения, характеризуемого значением  Величина М зависит также от "магн. предыстории" образца, что приводит к неоднозначности ф-ции M(H), или к гистерезису магнитному. При намагничивании и перемагничивании ферромагнетика происходит изменение. размеров и формы образца (см. Магнитострикция; )благодаря этому кривые намагничивания и петли гистерезиса зависят от внеш. напряжений. Наблюдаются также аномалии в величине и температурной зависимости упругих постоянных ферромагнетиков - т. н. DE-эффект и др. (см. Механострикция, Магнитомеха-нические явления), а также коэф. линейного и объёмного расширения. При адиабатич. намагничивании или размагничивании ферромагнетики изменяют свою темп-ру (см. Магнитокалорический эффект, Магнитное охлаждение). В ферромагн. монокристаллах наблюдается обычно резкая магнитная анизотропия (рис. 2). В поликрйсталлах с хаотич. распределением ориентации зёрен анизотропия в среднем по образцу отсутствует, но при однородном распределении этих ориентации она может возникать (см. Магнитная текстура). В результате конкуренции обменного и магн. дипольного взаимодействий происходит разбиение конечного ферромагн. образца наферромагнитные домены (см. также Магнитная доменная структура ).Магн. и др. физ. свойства (в т. ч. электрич., тепловые, гальваномагн., магнитооптические) ферромагнетиков обладают ярко выраженной зависимостью от темп-ры, особенно вблизи Т_C. Спонтанная (при H=0) намагниченность M_s имеет максимум при 0 К и монотонно стремится к нулю при (рис. 3). Выше Т_C ферромагнетик переходит в парамагн. состояние, а в нек-рых случаях (редкоземельные металлы)-в антиферромагнитное, что представляет собой частный случаймагнитного фазового перехода 2-го рода. Магнитная проницаемость (или магн. восприимчивость) ферромагнетиков имеет резко выраженный максимум вблизи Т_C; при Т> Т_C уд. восприимчивость c обычно следует Кюри - Вепса закону. В более общих случаях в ферромагнетиках могут происходить ориентаци-онные фазовые переходы, при к-рых перестраивается магнитная атомная структура и изменяется магнитная симметрияферромагнетика. Важный класс ферромагнетиков представляют собой магнитные сверхпроводники, в к-рых достигается сосуществование явлений Ф. и сверхпроводимости.

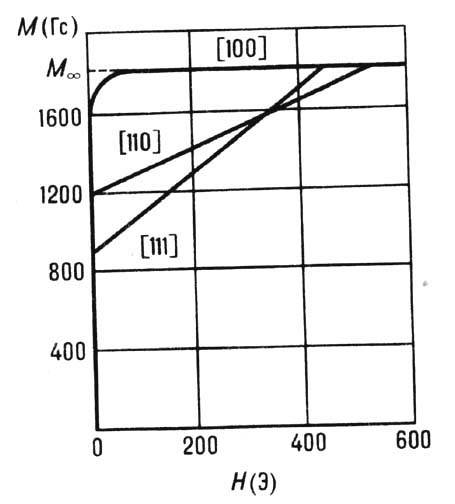
Рис. 2. Зависимость намагниченности М от магнитного поля для трёх главных кристаллографических осей монокристалла Fe (тип решётки - объёмнопентрированная кубическая, направление [100] -ось лёгкого, [110] - ось трудного и [111] - ось труднейшего намагничивания).

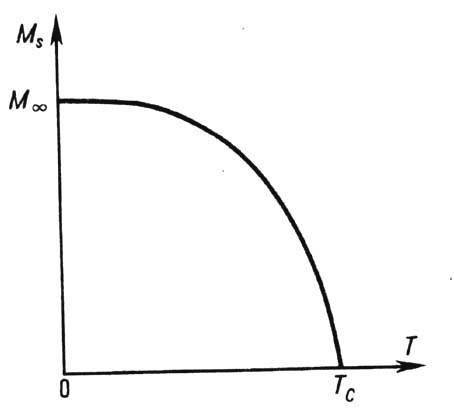
Рис. 3. Схематический ход температурной зависимости спонтанной намагниченности ферромагнетика; М_oo - значение M_s в состоянии магнитного насыщения, Т_C - точка Кюри.

Классификация и основные модели ферромагнетиков. Необходимый признак Ф. вещества - наличие постоянных (не зависящих от внеш. магн. полей) магн. (спиновых или орбитальных, либо тех и других вместе) моментов электронных оболочек у составляющих его атомов (ионов) (Fe, Со, Ni и др.). Однако при конденсации магнитно-активных атомов (ионов) в кристалл или аморфное тело их электронные оболочки часто претерпевают такую деформацию, что кристалл или аморфное тело уже не обладает в своих узлах пост. магн. моментами. Наиб. перестройке при конденсации подвергается самый наружный (валентный) слой электронной оболочки. Это обусловлено тем, что волновые ф-ции валентных электронов у соседних атомов в твёрдом теле сильно перекрываются, что приводит к коллективизации бывших валентных электронов. В случае металлов они при этом образуют ферми-газ (или ферми-жидкость)электронов проводимости, а в неметал-лич. веществах - локализованные спин-насыщенные связи. В обоих случаях, как правило, для осн. состояния (T=0 К и H = 0) намагниченность М=0. Если атомы, из к-рых построен образец, не относятся к переходным элементам, то электронная оболочка ионных остовов в соответствии с Паули принципом имеет замкнутый характер и обладает диамагнетизмом .Более детальные исследования с помощью ядерного магнитного резонанса, Мёссбауэра эффекта и ядерной теплоёмкости обнаружили на атомных ядрах (Fe, Co, Ni и др.) очень сильные магн. поля - до 10⁵ - 10⁶ Э, источником к-рых являются "деформированные" внутренние 1s-, 2s- и 3s-слои оболочки ионных остовов. Электроны проводимости, подмагниченные благодаря обменному взаимодействию с d- или f-слоями атомной оболочки, участвуют в спонтанной намагниченности ферромагнетика.

В случае, когда ферромагнетик построен из атомов переходных элементов, в нём возможно сохранение не зависящего от внеш. поля магн. момента. При этом можно различать 4 осн. типа веществ: 1) металлич. вещества (чистые металлы, сплавы и соединения) на основе переходных элементов с недостроенными d-слоями (прежде всего 3d-слоями у атомов группы Fe); 2) металлич. вещества на основе переходныхf-элементов [в первую очередь редкоземельных (РЗМ) с недостроенным 4f-слоем]; 3) неме-таллич. соединения при наличии хотя бы одного компонента из переходных d- или f-элементов; 4) сильно разбавленные растворы парамагн. ионов d- или f-элементов в диамагн. веществах. Появление во всех этих веществах атомного магн. порядка обусловлено обменным взаимодействием в магнетике. В неметаллич. веществах (тип 3) это взаимодействие носит косвенный характер (см. Косвенное обменное взаимодействие ),при к-ром магн. порядок электронных магн. моментов недостроенных d- или f-слоев в ближайших соседних парамагн. ионах устанавливается при активном участии электронов внешних замкнутых слоев магн--нейтральных ионов (О^2-, S^2-, Se^2- и т. п.), расположенных между магнитно-активными ионами. В большинстве случаев здесь устанавливается антиферромагн. порядок, к-рый может привести либо к чистому антиферромагнетизму ,если в каждой элементарной ячейке кристалла суммарный магн. момент всех ионов равен нулю, либо к ферримагнетизму или слабому ферромагнетизму, если он отличен от нуля. Есть такие случаи, когда взаимодействие и в неметаллич. веществах носит ферромагн. характер (все магн. моменты в ячейке параллельны). Общим для веществ типа 1, 2 и 4 является наличие в них системы ферми-частиц - коллективизированных (зонных) электронов проводимости. Эта система, хотя в ней существует подмагничивающая тенденция (обменные силы), как правило, не имеет магн. порядка и обладает парамагнетизмом Паули, если он не подавлен диамагнетизмом самих электронов проводимости или системы ионных остовов с замкнутыми оболочками. Парамагнетизм преобладает во всех непереходных металлах и большинстве переходных d-металлов (целиком группы Pd и Pt, а в группе Fe-у Sc, Тi и V).

Магн. порядок в металлич. веществах (тип 1, 2 и 4) различен по своему происхождению. Недостроенные 4f-слои ионов РЗМ-элементов (тип 2) имеют очень малый радиус по сравнению с параметром кристаллич. решётки, и поэтому волновые ф-ции этих электронов у соседних узлов в кристалле или у соседей в аморфном теле практически не перекрываются. Следовательно, в таких веществах невозможен сколько-нибудь существенный прямой обмен. Его также нельзя ожидать и между сильно удалёнными друг от друга парамагн. d- или f-ионами в сильно разбавленных сплавах (тип 4). Т. о., следует ожидать, что в веществах типа 2 и 4 энергетич. параметр (обменный интеграл) прямого обмена исчезающе мал. Поэтому в таких веществах обменное взаимодействие, приводящее к магн. атомному порядку, должно носить характер косвенной связи магн. ионов через электроны проводимости, или т. н. РККИ-обменного взаимодействия. Наконец, в веществах типа 1 электроны; принимающие активное участие в атомном магн. порядке, состоят из бывших 3d-и 4s-электронов изолир. атомов. В отличие от 4f-слоев РЗМ-ионов, имеющих очень малый радиус, более близкие к периферии 3d-электроны атомов группы Fe испытывают более существенную коллективизацию и совместно с 4s-электронами образуют общую ферми-жидкость электронов проводимости. Однако в отличие от нормальных (непереходных) металлов, эта система в d-металлах обладает гораздо большей плотностью состояний вблизи поверхности Ферми, что благоприятствует обменным силам в их конкуренции с размагничивающими "тенденциями" фер-ми-газа (см. Паули парамагнетизм)и приводит к Ф. в Fe, Со, Ni и их многочисл. сплавах и соединениях. В последнее время начали интенсивно исследоваться т. н. к о н д о в-с к и е ф е р р о м а г н е т и к и (CeRh₃Be₂, CeSi_x и др.), в к-рых f-электроны (обычно от Се) частично делокализуют-ся за счёт Кондо эффекта .Эти вещества по ряду свойств напоминают РЗМ-ферромагнетики, а по другим - зонные магнетики на основе d-металлов; не совсем обычными свойствами обладают и а к т и н и д н ы е м а г н е т и к и, среди к-рых встречаются ферромагнетики. 

В целом квантовая теория Ф. даёт возможность качественно понять возникновение Ф. как результата положит. обменного взаимодействия. Однако количественно она далека от завершения. В последовательной микроскопич. теории прежде всего нужно определить знак осн. энергетич. параметра обменного взаимодействия (e_об, см. в ст. Магнетизм). Для этого необходимо знать энергетич. спектр и волновые ф-ции системы электронов, участвующих в Ф. Однако пока точных сведений об этих величинах нет, и поэтому приходится пользоваться приближёнными подходами. Существуют 3 осн. модели Ф.: а) модель локализованных атомных магн. моментов (см. Гейзенберга модель, а также полярная модель и Хаббарда модель; )б) модель коллективизированных электронов, предложенная Я. И. Френкелем и Э. Стонером (Е. Stoner) (см. Стокера модель, Зонный магнетизм); в) s - d(f )-обменная модель (см. Шубина-Вонсовского модель и Зинера модель).В модели а) предполагается, что атомные магн. моменты жёстко локализованы около узлов решётки и не принимают участия в процессах переноса в веществе. Эта модель лучше всего подходит для описания магн. порядка в неме-таллич. веществах (тип 3). В модели б) предполагается, что в ферми-системе электронов проводимости сильная обменная связь делает энергетически более выгодным Ф. Эта модель лучше всего подходит для объяснения Ф. d-металлов. Наконец s-d (f)-обменная модель в известном смысле объединяет первые две, допуская подмагничи-вание системы электронов проводимости. Модель в) лучше всего подходит для описания веществ типа 2 и 4. Большое эвристич. значение имеет изучение сильно разбавленных растворов (тип 4), а также Кондо-решёток, поскольку выяснение условий "сохранения", а иногда и резкого увеличения магн. моментов в сплаве (за счёт поляризации окружающей атом примеси электронов проводимости диамагн. матрицы) по сравнению с их значением в изолир. парамагн. ионах может прояснить детали возникновения Ф. в d-металлах, их сплавах и соединениях.

Теория самопроизвольной намагниченности. Конкретные расчёты по всем трём моделям Ф. могут проводиться как в квазиклассич. и феноменологич. приближениях, так и с помощью квантовомеханич. методов, в т. ч. метода функционала спиновой плотности. При квазиклассич. описании Ф. учитывают введением молекулярного поля. В простейшем расчёте для газа из N электронных спинов (на основеИзинга модели)их можно разбить соответственно двум возможным проекциям на r "правых" и N-r = l "левых". Тогда относит. намагниченность системы "впра-во" равна y = (r-l)/N. Энтропия "газа" при пренебрежении взаимодействием между спинами равна S(y) = k]n(N\/rll! (k -Больцмана постоянная ).Если энергия "газа" U не зависит от у, то свободная энергия равна

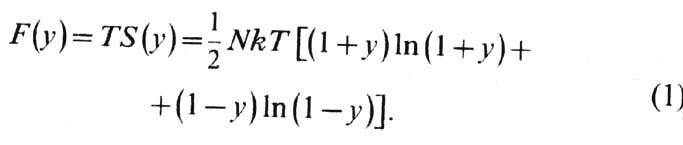
Из условия минимума (1) следует, что y = 0, т. е. Ф. отсутствует. Для его существования необходимо принять, что U зависит от у. В простейшем случае (гипотеза молекуляр-ного поля Вейса)

где А'>0-постоянная молекулярного поля, отнесённая к одному спину. Из условия минимума F(y)=-NA'y²-TS (у)находим:

где T_C = 2A'/k - точка Кюри. Ф-ла (3) даёт выражение для зависимости М_oo (Т)при H=0, качественно согласующееся с кривой на рис. 3.

В квазиклассич. и феноменологич. подходе были даны многочисл. уточнения приведённого расчёта. В частности, проводился учёт ближнего магн. порядка (м е т о д Б ет е - П а й е р л с а - В е й с а), развита термодинамич. теория ферромагн. превращения (см. Ландау теория), в рамках к-рой был также рассмотрен вопрос о температурной зависимости разл. физ. свойств ферромагнетиков вблизи точки Кюри. Последние обычно описываются степенным законом типа (Т-Т_C)^a, где показатель степени a наз. критическим показателем. Эти показатели для намагниченности, теплоёмкости, восприимчивости вычисляются в рамках моделей Изинга, Гейзенберга и более общих схем по Ландау, а также на основе ренормализационной группы по Вильсону (см. Эпсилон-разложение ).Более строгое уточнение приведённого выше расчёта далаквантовая механика, оправдавшая выбор зависимости (2) и объяснившая физ. природу параметра А' как меры обменной связи, зависящей от взаимной ориентации электронных спинов. Согласно Дираку (см. Обменное взаимодействие и Гейзенберга модель ),оператор обменной энергии системы электронных спинов имеет вид

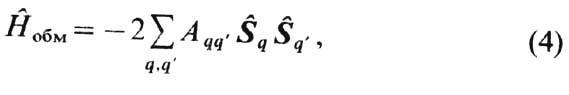
где  -оператор вектора спина атома в узле q; A_qq'-- интеграл обмена между электронами в узлах q и q'. Если A_qq' резко падает с расстояниями между узлами, то можно ограничиться приближением ближайших соседей и, введя обозначение А_q,qb1=А, написать (4) в форме

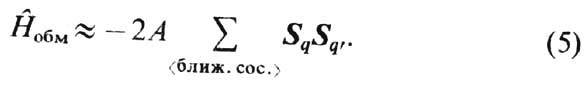
Квадрат суммарного спина всех N электронов равен

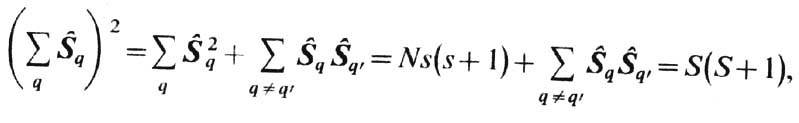
где S-полное спиновое квантовое число системы, a s - одного узла. Число членов парных произведений равно N(N-1). Поэтому ср. значение отд. члена этой суммы равно

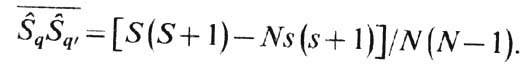
Число членов в сумме (5) равно (l/2)zN, где z-число ближайших соседей у узла решётки. Т. о., ср. значение гамильтониана системы равно

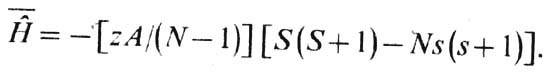
Поскольку s~ 1, a S-порядка намагниченности всей системы M=Ny (в единицах магнетона Бора m_B), то в ферромагнетике с точностью до членов ~1/N

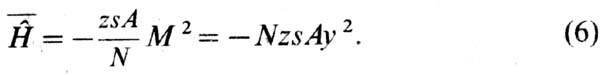
Этот расчёт проведён в т. н. п р и б л и ж е н и и э н е р г е т и ч е с к и х ц е н т р о в т я ж е с т и [4]. Из сравнения (6) и (2) видно, что параметр А' квазиклассич. теории определяется обменной энергией А, т. е. A' = zsA. Для определения величины и знака А нужна более точная теория, к-рую дают, напр., микроскопич. расчёты обменных взаимодействий в металлах методом функционала спиновой плотности, исходя лишь из кристаллич. структуры и порядкового номера в таблице Менделеева [11]. Используются также нек-рые усложнения гейзенберговского гамильтониана, напр. с помощью учёта неск. типов обменных интегралов между разл. соседями в узлах решётки (подробнее см. Спиновый гамильтониан ).При низких Т, используя метод вторичного квантования, удалось провести более точный расчёт энергетич. спектра ферромагнетика. Ограничиваясь состояниями, близкими к основному (при О К), в к-ром спины всех магнитно-активных электронов взаимно параллельны, можно найти собств. значения оператора (5), имеющие вид суммы энергий отд. элементарных возбуждений (квазичастиц) - спиновых волн, или ф е р р о-м а г н о н о в. Каждый ферромагнон несёт с собой магн. возбуждение системы и уменьшает  на величину магн. момента одного узла решётки. С ростом Т возбуждается всё больше спиновых волн. Пока их мало, они образуютидеальный газ бозевских квазичастиц (см. Бозоны; )с ростом Т их число растёт ~T^3/2; поэтому температурная зависимость   вблизи 0 К имеет вид

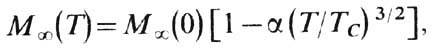
где   -предельное значение   при 0 К (см. Блоха закон ).Знание спектра спиновых волн важно для изучения явления ферромагнитного резонанса, распространения упругих колебаний в ферромагнетике и всего комплекса физ. свойств при низких темп-рах.

Применение квантово-статистич. методов (см. Грина функция, Матрица плотности)открывает новые возможности для построения более точной микроскопич. теории Ф. В частности, в рамках локализов. модели из этой теории следует, что при 0 К ср. атомный магн. момент, приходящийся на один узел, должен быть кратен m_B. Однако опыт показывает, что особенно в d-металлах, сплавах и соединениях эта величина заметно меньше момента изо-лир. атома (иона) и, кроме того, она существенно дробная (в единицах m_B). Это противоречие модели локализов. спинов с опытом связано с пренебрежением коллективизацией 3d-электронов в металле, а также обменным s - d (f)-взаимодействием.

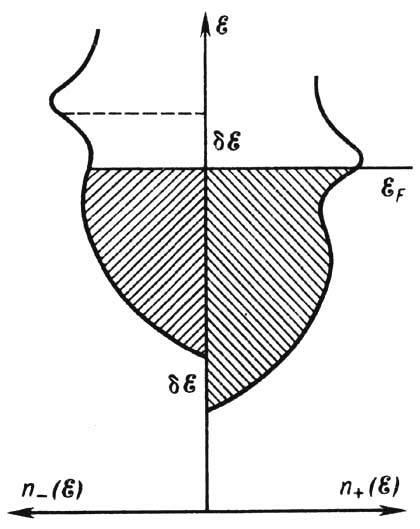
Рис. 4. Схематическое изображение смещения на   кривых плотностей электронных состояний пb( )для "правых" ( + ) и "левых" ( -) спинов, обусловленного обменным взаимодействием, в энергетической полосе проводимости d-металла;  - ферми-энергия.

В рамках зонной модели Ф. эта трудность в принципе исчезает (см. Зонный магнетизм ).Ф. в ферми-газе возможен при спонтанном "сдвиге" на   энергии уровней в подполосе для "правых" и "левых" спинов, обусловленном обменным взаимодействием (рис. 4). При таком сдвиге, для того чтобы в равновесии ферми-энергия   в подполосах была одинаковой, надо v электронов на атом перенести из левой подполосы в правую. Это увеличивает кинетич. энергию на атом на величину   (если число v не очень велико). Обменная энергия определяется связью пар электронов; она пропорц. квадрату числа электронов в каждой подполосе (числа электронов в единице объёма в правой и левой подполосах равны п₊ и п_). В парамагн. состоянии п₊=п_=п/2. Изменение энергии системы при переходе из пара- в ферромагн. состояние равно

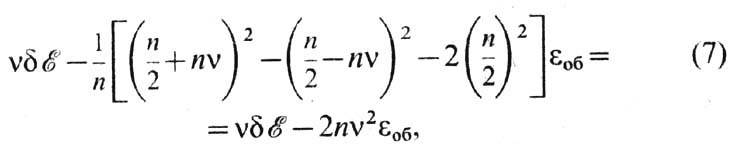
где e_об-ср. обменная энергия на пару электронов. Отношение   определяет плотность электронных уровней (рис. 4) около ферми-энергии . Если ввести безразмерный параметр  , то из (7) следует, что при h> 1 в равновесии имеет место Ф., а при h<1-парамагнетизм. Условие, или критерий, для Ф. (h>1) легче выполняется в металлах с большими плотностями состояния при  и большей энергией e_об. Из рис. 4 видно, что ср. атомный момент отнюдь не должен быть целочисленным в единицах m_B и равняться его значению для изолир. атома (иона).

Недостатком зонной модели является неучёт корреляц. энергии, к-рая может существенно изменить все количеств. и даже качеств. оценки приведённого расчёта (напр., критерий Ф.). Получены и более точные результаты, напр. при использовании метода расчёта с функционалом спиновой плотности. Помимо этого, зонная модель Ф. получила существ. развитие в работах, начатых Мория [22], в к-рых был произведён учёт спиновых флуктуации в ферромагн. системе электронов проводимости металлов и сплавов.

s - d(f)-обменная модель позволяет учесть не только пассивную роль электронов проводимости (напр., их под-магничивание со стороны "магнитных" f-слоев в РЗМ-ме-таллах), но и их активное участие в самом процессе установления Ф. благодаря косвенному РККИ-взаимодейст-вию. Качественно это можно описать так. Если ср. относит. намагниченность d(f)-электронов на узел равна m_d(f), а электронов проводимости-m_s, то энергия s - d(f)-обмена на узел равна   , где A_sd(f) - параметр s -d(f)-связи. Добавка к ферми-энергии, связанная с намагниченностью электронов проводимости, равна (1/2)А_Фт_s², где   и  - спиновая парамагн. восприимчивость (см. Паули парамагнетизм ).При квадратичном законе дисперсии электронов   , так что  . Полная энергия на узел, зависящая от m_d(f) и m_s, равна

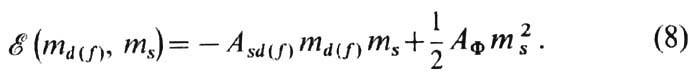
Энтропия сильно вырожденного газа электронов проводимости в металлах очень мала; поэтому равновесные значения m_d(f) и m_s находят из условия минимума энергии (8) при условиях:   и  . Одно из возможных решений имеет вид

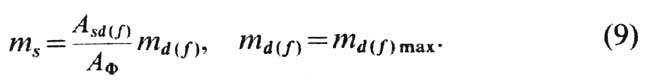
Отношение   ; m_s составляет  от  . Подстановка (9) в (8) даёт

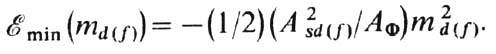
Т. о., эфф. параметр косвенного обмена типа РККИ между внутренними d(f)-электронами, взаимодействующими с электронами проводимости, равен

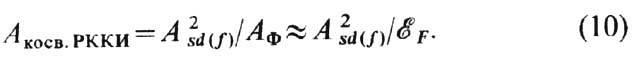
В данном приближении он всегда >0, т. е. способствует Ф. Более точный расчёт (10) показывает, что обмен типа РККИ сравнительно дальнодействующий (~ 1/r³) и носит осциллирующий знакопеременный характер.

Обменная s - d(f)-модель позволяет также установить связь между электронами проводимости РЗМ-металлов и особенностями их атомной магн. структуры, к-рая имеет вид неколлинеарных винтовых структур. Эта модель, если её дополнить учётом магн. (спин-орбитального) взаимодействия, позволяет также объяснить в принципе все аномалии электронных свойств ферромагнетиков, связанных с существованием в них спонтанной намагниченности. Учёт магн. (релятивистских) взаимодействий позволяет объяснить природу магн. анизотропии и магнитострикции.

Ещё в 1947 Ж, М. Латтинжер и Л. Тисса [12] высказали гипотезу о возможности существования "дипольного ферромагнетизма" в системе свободно вращающихся магн. диполей даже в отсутствие обменного взаимодействия или при весьма слабом обменном взаимодействии. Экспериментально такой Ф. обнаружен в 1990 [13] в образце ГЦК-структуры РЗМ-соли Cs₂NaR(NO₂)₆ (где R = Dy, Er, Gd, Nd), в к-рой магн. ионы находятся на достаточно удалённом расстоянии и поэтому обменная связь (~10 мК) на порядок меньше дипольной энергии (~100 мК), а точки Кюри расположены в интервале   К.

Теория кривой намагничивания ферромагнетиков.

Из опыта известно, что при H=0 термодинамическому устойчивому состоянию макрообразца (минимуму термодинамич. потенциала) отвечает размагниченное состояние, ибо в противном случае на поверхности образца, как правило, образуются магн. полюса, создающие размагничивающее поле , с к-рым связана большая положит. энергия. Т. о., возникает тенденция размагничивания конечных образцов, хотя обменные силы стремятся их "намагнитить".

В результате происходит разбиение фсрромагн. образца на макрообласти однородной намагниченности. Эту гипотезу высказал ещё в 1907 П. Вейсс (P. Weiss), а количественно обосновали впервые в 1935 Л. Ландау и Е. Лифшиц (см. Ферромагнитные домены и Магнитная доменная структура). Теория Ф. качественно определяет размеры и форму доменов, к-рые зависят от конкуренции разл. взаимодействий внутри ферромагнетика. Равновесная структура доменов при Н=0 имеет вид совокупности связанных замкнутых магн. потоков внутри образца. Наряду с осн. доменами могут возникать и вторичные, т. н. з а м ы к а ю щ и е, домены. Магн. доменная структура является весьма структурно чувствительной. Между доменами образуются промежуточные слои, или стенки (см. Доменная стенка, Блоха стенка, Нееля стенка), конечной толщины, в к-рых вектор   непрерывно меняет своё направление от ориентации, отвечающей вектору   в одном домене, до ориентации, отвечающей направлению  его соседа. На образование этих стенок затрачивается положит. энергия, но её величина по всему образцу меньше энергии поля  , к-рая возникла бы в отсутствие доменов. При нек-рых критически малых размерах ферромагн. образцов возникновение в них неск. доменов может стать энергетически невыгодным, тогда частицы остаются при Т<Т_Cоднородно намагниченными (см. Однодоменные частицы ).Этим объясняются особые свойства тонких ферромагн. порошков и изделий из них (см. Магнитно-твёрдые материалы ).Среди них получили довольно широкое распространение коллоидные растворы однодоменных ферромагн. частиц, образующих магн. жидкости, имеющие перспективные области применения в технике и медицине. Весьма специфич. характер носит ферромагн. доменная структура в гонкой магнитной плёнке (см. также Цилиндрические магнитные домены). Кривые намагничивания и петли гистерезиса в ферромагнетиках, т. е. все процессы перемагничивания, определяются, в первую очередь, изменениями доменной структуры во внеш. магн. поле H, т. е. путём изменения объёма доменов с разл. ориентацией векторов  в них за счёт смещения границ доменов (см.Доменной стенки динамика, Доменопродвигаюшая структура). Кроме того, играет роль и вращение векторов   в направлении внеш. поля. В размагниченном состоянии (с точностью до объёма, занятого доменными стенками) имеем

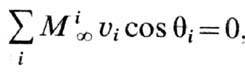
, где суммирование идёт по всем i-м доменам; u_i - объём i-го домена; q_i-угол между вектором   в i-м домене и любой фиксир. осью в образце, напр. совпадающей с ориентацией намагничивающего поля. При включении поля вдоль этой оси в направлении поля появляется отличная от нуля намагниченность:

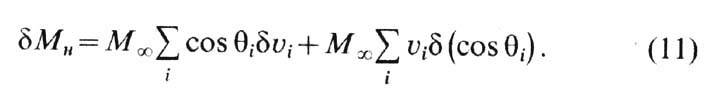
Первое слагаемое в (11) обусловлено ростом объёмов доменов,   в к-рых направлены относительно Н энергетически более выгодно, за счёт объёмов доменов, намагниченных менее выгодно; всё это осуществляется путём процессов смещения доменных стенок. Второе слагаемое в (11) обусловлено процессами вращения векторов  . Уд. магн. восприимчивость ферромагнетиков, т. о., приближённо равна сумме  Анализ реальных кривых показывает, что в слабых полях  а в более сильных (после крутого подъёма кривой)  При размагничивании ферромагнетика из состояния магн. насыщения происходит восстановление доменной структуры путём возникновения з а р о д ы ш е й п е р е м а г н и ч и-в а н и я - областей с обратной (по отношению к первоначальной) намагниченностью. В. Дёрингом (W. Doring) в 1939 была разработана достаточно строгая и общая теория роста таких зародышей, к-рая хорошо подтверждена экспериментально [9, 4].

Из-за структурной чувствительности доменной структуры и процессов намагничивания и перемагничивания количеств. теория кривых намагничивания и петель гистерезиса ферромагнетиков находится в нач. стадии развития. Лишь в случае расчёта кривых намагничивания идеальных монокристаллов определ. формы в области, где  [1 ], можно развить строгую количеств. теорию для образцов простой формы (напр., эллипсоидов), допускающей однородность намагниченности при их структурной и хим. однородности. Теория кривых намагничивания и петель гистерезиса имеет важное значение для разработки новых и улучшения существующих магнитных материалов, играющих весьма важную и всё возрастающую роль в совр. технике (напр., в магн. дефектоскопии и структурном анализе, а также при конструировании элементов памяти ЭВМ, ускорительных секций, накопительных колец и т. п.).

42.Свободные электромагнитные колебания в колебательном контуре.

Колебательным контуром в общем случае называется электрическая цепь, состоящая из последовательно соединенных и конденсатора с емкостью  (с емкостным сопротивлением  ), катушки с индуктивностью  (с индуктивным сопротивлением  ) и электрического (активного) сопротивления  . Полное сопротивление цепи  . Электромагнитные колебания распространяются по цепи с огромной скоростью, равной скорости света  , . Пусть  частота колебаний в контуре. Если линейные размеры  контура не слишком велики  , то мгновенные значения силы тока во всех сечениях цепи будут практически одинаковыми. Такой переменный ток называетсяквазистационарным.Мгновенные значения квазистационарных токов подчиняются закону Ома; для них справедливы правила Кирхгофа.

В простейшем идеализированном случае, когда можно пренебречь электрическим сопротивлением, колебательный контур состоит из последовательно соединенных и конденсатора с емкостью  , катушки с индуктивностью  . Колебания в контуре можно вызвать, если:

· зарядить конденсатор и замкнуть его на катушку, то к контуре возникнет быстропеременный ток.

· возбудив в индуктивности ток (например, путем выключения внешнего магнитного поля, пронизывающего витки катушки).

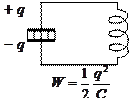
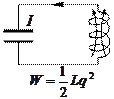Стадии колебательного процесса в контуре без активного сопротивления:

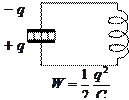
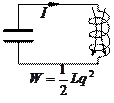
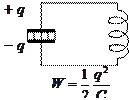
Присоединим отключенный от индуктивности конденсатор к источнику напряжения. Это приведет к возникновению на обкладках разноименных зарядов  и  (рис 1). Между обкладками возникнет электрическое поле, энергия которого  . Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но возникнет все возрастающая энергия магнитного поля, обусловленного током, текущим через индуктивность. Эта энергия равна  . В момент, когда напряжение на конденсаторе (и энергия электрического поля) обращаются в нуль, энергия магнитного поля (и ток) достигают наибольшего значения (рис. 2 – начиная с этого момента ток течет засчет э.д.с. самоиндукции). Далее ток уменьшается, и, когда заряды на обкладках достигнут первоначального значения  , сила тока станет равной нулю (рис.3). Затем те же процессы протекают в обратном направлении (рис.4 и 5), после чего система приходит в исходное состояние (стадия 5) и весь цикл повторяется. Полная энергия электромагнитных колебаний не изменяется с течением времени.  . В колебательном контуре происходит взаимное превращение энергий электрического и магнитного полей: при разрядке конденсатора энергия электрического поля конденсатора переходит в энергию магнитного поля катушки; последующая зарядка конденсатора зарядами противоположного знака происходит вследствие перехода энергии магнитного поля катушки в энергию электрического поля конденсатора и т.д.

В колебательном контуре могут происходить периодические изменения заряда  , разности потенциалов  на обкладках конденсатора и электрического тока  в цепи.

Взаимные превращения энергий электрического и магнитного полей сопровождаются потерями на нагревание проводников (в механической модели это соответствует потерям энергии из-за трения). Вследствие наличия энергетических потерь колебания переменного тока в контуре при однократной его зарядке затухают – амплитуда каждого последующего колебания переменного тока в этом случае несколько меньше амплитуды предыдущего колебания. Время затухания тем меньше, чем больше активное (омическое) сопротивление цепи, т.к. в этом случае больше потери энергии на нагревание проводов.

Исследование электромагнитных колебаний удобно производить, пользуясь тем, что колебания различной природы – механические и электромагнитные – подчиняются сходным закономерностям. Пользуются аналогиями, которые существуют между физическими величинами, характеризующими механические системы и электрические контуры (цепи):

МЕХАНИЧЕСКАЯ СИСТЕМА	ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
Масса	Индуктивность
Коэффициент квазиупругой силы	Величина, обратная электроемкости,
Коэффициент трения	Сопротивление
Сила	Э.д.с.
Смещение	Заряд
Скорость	Сила тока
Ускорение	Скорость изменения силы тока

 

Напишем для цепи закон Ома:  . В нашем случае  ,  ,  . Получаем, что изменение электрического заряда  на обкладках конденсатора со временем описывается дифференциальным уравнением:  . Если время отсчитывать от момента, когда разность потенциалов на обкладках конденсатора равна нулю, то решение этого уравнения имеет вид (при  ):  , где  амплитуда затухающих колебаний,  циклическая частота колебаний и  ,  коэффициент затухания,  начальные амплитуда и фаза (определяются из начальных условий). Величина  называется логарифмическим декрементом затухания(здесь  амплитуда соответствующей величины). Он обратен числу колебаний  , совершаемых за время, в течение которого амплитуда уменьшается в  раз .Считая  , получим  . Т.о. логарифмический декремент затухания является характеристикой контура. Добротность колебательного контура  ,. В случае слабого затухания  , получаем  и  , тогда  .

Периодическое изменение заряда на обкладках конденсатора вызывает переменный электрический ток  , переменную разность потенциалов на обкладках  , переменные электрические и магнитные поля. Свободные колебания  и  называются свободными электромагнитными колебаниями. При  в момент  энергия колебаний равна электрической энергии поля конденсатора. За счетвыделения джоулева тепла в контуре энергия электромагнитных колебаний уменьшается (рассеивается) и они затухают.

43.Переменный электрический ток. Резонанс токов и напряжений. Мощность в цепях переменного тока.

.12. Резонанс напряжений

Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника.

В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механической системе. Однако полная аналогия - равенство собственной частоты колебаний электрического контура частоте возмущающей силы (частоте напряжения сети) — возможна не во всех случаях.

В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи представляет собой активное сопротивление. Такое состояние цепи имеет место при определенном соотношении ее параметров r, L, С, когда резонансная частота цепи равна частоте приложенного к ней напряжения.

Резонанс вэлектрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот.

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках. В цепи, где r, L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r, L, С соединены параллельно,— резонанс токов.

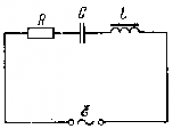
Рассмотрим явление резонанса напряжений на примере цепи рис. 2.11, а.

Как отмечалось, при резонансе ток и напряжение совпадают по фазе, т. е. угол φ = 0. и полное сопротивление цепи равно ее активному сопротивлению.

z = √r² + (x_L - x_С)² = r.

Это равенство, очевидно, будет иметь место, если x_L = х_С , т. е. реактивное сопротивление цепи равно нулю:

x = x_L — x_С = 0.

Выразив x_L и x_С соответственно через L, С и f, получим

2πfL =	1	,
	2πfC

откуда

f =	1	= fрез
	2π√LC

где f — частота напряжения, подведенного к контуру; f_рез — резонансная частота.

Таким образом, при x_L = x_С в цепи возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи.

Из   выражения   закона   Ома  для   последовательной   цепи

I =	U	.
	√r2 + (xL - xС)2

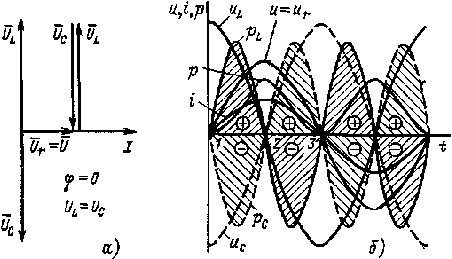
Рис. 2.14. Векторная диаграмма (а) и графики мгновенных значений и, i, р (б) цепи рис. 2.11, а при резонансе напряжений

вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление:

I = U/r.

Ток в цепи может оказаться значительно больше тока, который был бы при отсутствии резонанса. При резонансе напряжение на индуктивности равно напряжению на емкости:

Ix_L = Ix_С = U_L = U_C.

При больших значениях x_L и х_C относительно r эти напряжения могут во много раз превышать напряжение сети. Резонанс в цепи при последовательном соединении потребителей носит название резонанса напряжений.

Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

U_r = Ir = U.

На рис. 2.14, а изображена векторная диаграмма цепи рис. 2.11, а при резонансе напряжений Диаграмма подтверждает тот факт, что ток совпадает по фазе с напряжением сети и что напряжение на активном сопротивлении равно напряжению сети. Реактивная мощность при резонансе равна нулю:

Q = Q_L - Q_C = U_LI - U_CI = 0.

так как U_L = U_C.

Полная мощность равна активной мощности;

S = √P² + Q² = P,

так как реактивная мощность равна нулю. Коэффициент мощности равен единице:

cos φ = P/S = r/z = 1.

Поскольку резонанс напряжений возникает, когда индуктивное сопротивление последовательной цепи равно емкостному, а их значения определяются соответственно индуктивностью, емкостью цепи и частотой сети,

xL = 2πfL,   xС =	1	.
	2πfС

Резонанс может быть получен или путем подбора параметров цепи при заданной частоте сети, или путем подбора частоты сети при заданных параметрах цепи.

На рис. 2.14, б изображены графики мгновенных значений тока i, напряжения и сети и напряжений и_L , и_C , и_r на отдельных участках, а также активной р = iu_r и реактивной p_L= iи_L ,  p_С = iи_С мощностей за период для цепи рис. 2.11. а при резонансе напряжений. С помощью этих графиков можно проследить энергетическне процессы, происходящие в цепи при резонансе напряжений.

Активная мощность р все время положительна, она поступает из сети к активному сопротивлению и выделяется в нем в виде тепла. Мощности p_L и р_С знакопеременные, и, как видно из графика, их средние значения равны нулю.

В момент времени t = 0 (точка I на рис. 2.14, б) ток в цепи i = 0 и энергия магнитного поля  W_L = 0. Напряжение на емкости равно амплитудному значению U_тС, конденсатор заряжен и энергия его электрического поля

WC =	U2тcС	.
	2

В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на емкости и, следовательно, энергия электрического поля убывают. Ток в цепи и энергия магнитного поля возрастают.

В конце первой четверти периода (точка 2) и_С = 0, W_С = 0. i = I_m,  W_L = I²_mL/2.

Таким образом, в первую четверть периода энергия электрического поля переходит в энергию магнитного поля.

Так как площади p_С(t) и p_L(t) , выражающие запас энергии соответственно в электрическом и магнитном  полях, одинаковы, вся энергия электрического поля конденсатора переходит в энергию магнитного поля индуктивности. Во вторую четверть периода, в интервале между точками 2 и 3, энергия магнитного поля переходит в энергию электрического поля.

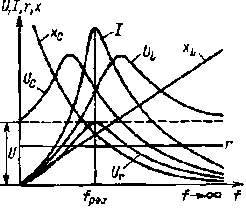
Рис. 2.15. Графики зависимости I, r, хC, хL, Ur, UL , UC от частоты цепи, изображенной на рис  2.11, а

Аналогичные процессы происходят и в последующие четверти периода.

Таким образом, при резонансе реактивная энергия циркулирует внутри контура от индуктивности к емкости и обратно. Обмена реактивной энергией между источниками и цепью не происходит. Ток в проводниках, соединяющих источник с цепью, обусловлен только активной мощностью.

Для анализа цепей иногда используют частотный метод, позволяющий выяснить зависимость параметров цепи и других величин oт частоты.

На рис 2.15 изображены графики зависимости U_r, U_C, U_L , I, х_C , х_L , от частоты при неизменном напряжении сети.

При f = 0 сопротивления x_L = 2πfL = 0, х_C = 1/2πfC = ∞, ток I = 0, напряжения U_r = I_r = 0,  U_L = Ix_L= 0, U_C = U.  При f = f_pез х_L = х_C , I = U/r, U_L = U_C, U_r = U. При f→ ∞ x_L→∞, х_C→ 0, U_r → 0, U_C → 0, U_L → U.

В интервале частот от f = 0 до f = f_pез нагрузка имеет активно-емкостный характер, ток опережает по фазе напряжение сети. В интервале частот f = f_pез до f→ ∞ нагрузка носит активно-индуктивный характер, ток отстает по фазе от напряжения сети.

Наибольшее значение напряжения на емкости получается при частоте, несколько меньшей резонансной, на индуктивности - при частоте, несколько большей резонансной.

Явления резонанса широко используются в радиоэлектронных устройствах и в заводских промышленных установках.

Пример 2.4. Определить частоту сети, при которой в цепи рис. 2.11, а возникает резонанс напряжений. Определить также, во сколько раз напряжение на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры:

r = 20 Ом, L = 0,1 Гн, С = 5 мкф.

Решение. Резонансная частота

fpез =	1	=	1	= 224 Гц.
	2π√LC		2•3,14•√0,1•5•10-6

Индуктивное сопротивление цепи при резонансе

x_L = 2πf_pезL - 6,28 • 224 • 0,l = 140 Ом.

Напряжение на индуктивности при резонансе

UL	=	IxL	,    UL = U	xL	= U	140	= 7U.
U		Ir		r		20

Напряжение на индуктивности при резонансе в 7 раз больше напряжения сети.

Резонанс в электрической цепи.
Резонанс в электрической цепи — явление резкого возраста­ния амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного кон­тура.
Из выражения для полного сопротивления переменному току  видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии   или  .
Следовательно,   - т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.
Амплитуды колебаний напряжения на индуктивности и емкости будут равны   и  - т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p).
Следовательно,  .
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет опреде­ляться уравнением  .  В этом и состоит смысл явления резонанса.
При этом если величина  ,  то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)!
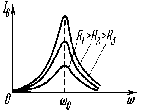
На рисунке представлена зависимость тока в колеба­тельном контуре от частоты при значениях R, где R1<R2<R3.
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа  .
В случае резонанса  . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников  на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.).

44.45.Вихревое электрическое поле. Первое уравнение Максвелла. Применение и наблюдение вихревых полей.

Как мы знаем из закона электромагнитной индукции Фарадея, в замкнутом контуре индуцируется ЭДС при изменении магнитного потока, пронизывающего этот контур

. (3.93)

Если контур (проводник) движется, то причиной возникновения ЭДС может быть сила Лоренца. Если же контур неподвижен, то и в этом случае, как показывает опыт, в нём возникает ЭДС, определяемая уравнением (3.93). Какова же в этом случае причина возникновения ЭДС? Под действием ЭДС в контуре возникает электрический ток. Это значит, что на электроны проводника действует электрическое поле. Если контур жёсткий, то можно записать

,

или

. (3.94)

(Мы поставили знак частной производной, поскольку магнитная индукция может зависеть и от координаты и от времени.) Из 14.2 следует, что циркуляция этого поля по замкнутому контуру не равна нулю, в отличие от электростатического поля. Максвелл предположил, что изменяющееся во времени магнитное поле порождаетвихревое электрическое поле, независимо от того, имеется у нас проводящий контур или нет. Просто если он есть, то позволяет зарегистрировать вихревое электрическое поле Е_В.

Левую часть уравнения (3.94) можно преобразовать по формуле Стокса  . Тогда, вместо уравнения (3.94), получим

. (3.95)

Поскольку интегрирование может производиться по любой поверхности, опирающейся на контур L, то в каждой точке этой поверхности должны равняться подынтегральные выражения

. (3.96)

Поле Е_В существенно отличается от электростатического поля, для которого, как мы помним, циркуляция по замкнутому контуру равна нулю:  , а значит, в соответствии с теоремой Стокса, и ротор этого поля в любой точке равен нулю:

. (3.97)

В общем случае

, (3.98)

но для ротора суммарного поля, в силу уравнения (3.97), остаётся справедливым соотношение (3.96). Таким образом,

. (3.99)

Поскольку переменное магнитное поле порождает электрическое, как это следует из закона индукции Фарадея и полученной нами из этого закона формулы (3.99), то должно существовать и обратное явление – переменное электрическое поле должно порождать магнитное поле. Для установления количественных соотношений рассмотрим процесс заряда конденсатора.

Рисунок 3.21

Для начала определим поле вблизи поверхности металлической обкладки конденсатора. Применим терему Гаусса для вектора электрического смещения к одной из обкладок (рис. 3.21). Внутри металла поле равно нулю, а снаружи направлено перпендикулярно поверхности. Следовательно, поток через весь цилиндр сведётся к потоку через верхнее основание цилиндра площадью dS. И этот поток должен равняться заряду, заключённому внутри нашего цилиндра, или DdS=sdS, или

D=s . (3.100)

Здесь s – поверхностная плотность зарядов на обкладке конденсатора.

Как мы уже говорили, Максвелл предположил, что изменяющееся электрическое поле создаёт магнитное поле. Но мы знаем, что постоянное магнитное поле создаётся токами. Поэтому естественно предположение, что должен быть ещё один ток, который Максвелл назвал током смещения и который ответственен за создание магнитного поля. Для установления вида этого тока смещения, рассмотрим соотношение (3.100) справа налево, а именно

s =D. (3.101)

Умножим обе части на площадь пластины S и получим

q=sS= DS. (3.102)

Здесь q – заряд пластины конденсатора. Во время заряда конденсатора ток в подводящем проводе

. (3.103)

Разделив обе части последнего уравнения на площадь пластины S, получим слева ток проводимости j=I/S, а справа – плотность нового, максвелловского тока, или плотность тока смещения. Таким образом,

. (3.104)

В последнем уравнении мы поставили значки векторов – для общего случая и написали частную производную, поскольку в общем случае вектор электрического смещения может зависеть и от координаты.

Проанализировав полученные результаты, Максвелл ввёл понятие общего тока как суммы токов проводимости и тока смещения. Здесь подчеркнём, что ток смещения – это просто название изменяющегося во времени электрического поля. Единственная функция тока смещения – создавать магнитное поле. Тогда обобщенный закон полного тока будет иметь вид

, (3.105)

или окончательно

. (3.106)

Максвелл создал замкнутую макроскопическую теорию электромагнитного поля. В основе этой теории лежат его знаменитые уравнения. Первая пара связывает основные характеристики электрического и магнитного полей

; (3.107)

 

. (3.108)

В уравнении (3.107) под полем E надо понимать полное поле – поле, созданное неподвижными зарядами, и поле, созданное изменяющимся магнитным полем. Уравнение (3.108) отражает тот факт, что в природе нет магнитных зарядов.

Вторая пара уравнений Максвелла связывает вспомогательные характеристики электрического и магнитного полей

; (3.109)

 

. (3.110)

Уравнение (3.109) является следствием того, что магнитное поле создаётся как токами проводимости, так и токами смещения (изменяющимся во времени электрическим полем). И уравнение (3.110) говорит нам, что источниками электрического поля (помимо изменяющегося магнитного поля) являются электрические заряды. Уравнения Максвелла (3.107)…(3.110) называются уравнениями Максвелла в интегральной форме.

 

Уравнения Максвелла дополняются так называемыми материальными уравнениями, которые устанавливают связь между вспомогательными и основными характеристиками полей. Для однородной и изотропной неферромагнитной среды эти уравнения имеют вид

 (3.111)

Уравнения Максвелла не симметричны относительно электрического и магнитного полей, поскольку в природе нет магнитных зарядов.

Уравнения Максвелла позволили предсказать существование электромагнитных волн – распространяющихся в пространстве со скоростью света переменных электрического и магнитного полей. Вскоре электромагнитные волны были обнаружены немецким физиком Г.Герцем. Оказалось, что их свойства полностью описываются уравнениями Максвелла. Это также позволило Максвеллу создать электромагнитную теорию света – как электромагнитных волн с длиной волны  .

Если применить к уравнениям (3.107)…(3.110) теоремы Гаусса и Стокса, то получим уравнения Максвелла в дифференциальной форме:

; (3.112)

; (3.113)

; (3.114)

. (3.115)

Уравнения (3.98)…(3.101) связывают локальные характеристики поля в каждой точке.

.

46.Система уравнений Максвелла.
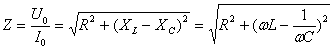
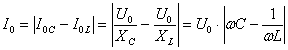