1) По первой строке, 2)по второму столбцу.
Решение.
1)
.
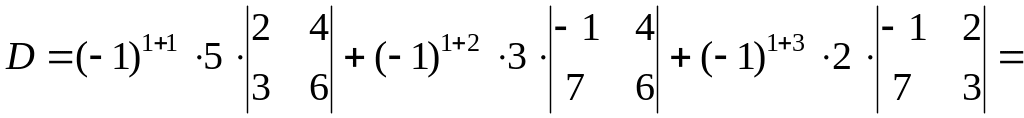
2)
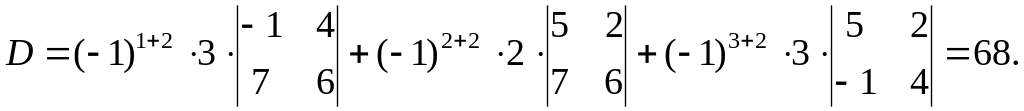
Для системы трех линейных уравнений с тремя неизвестными
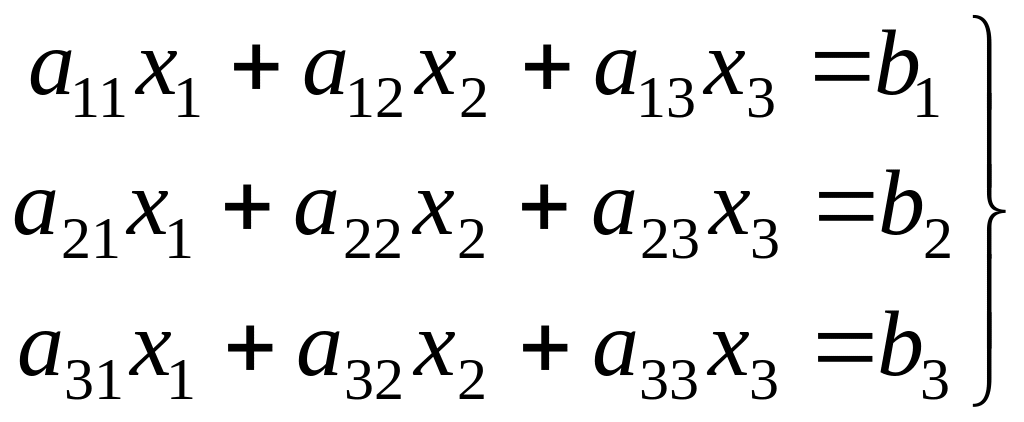
формулы
Крамера приобретают вид
.
Здесь
,
,
.
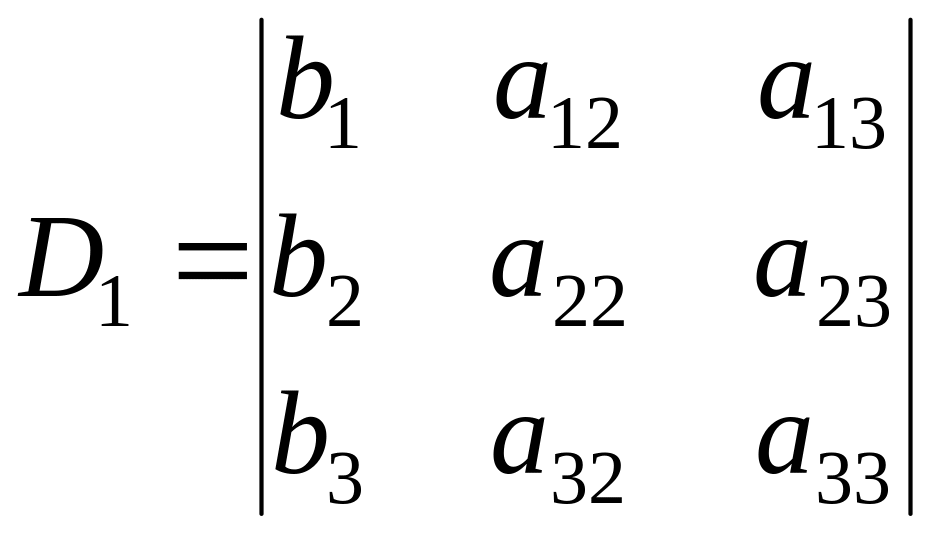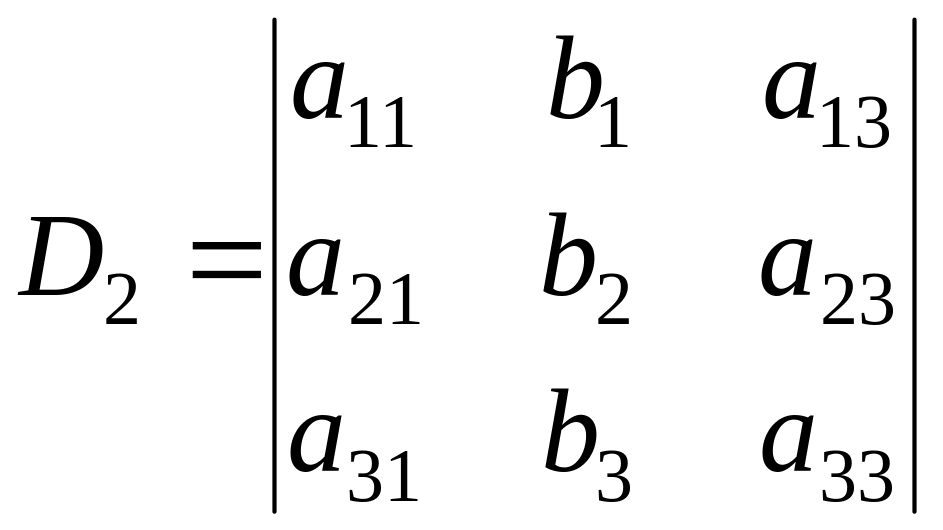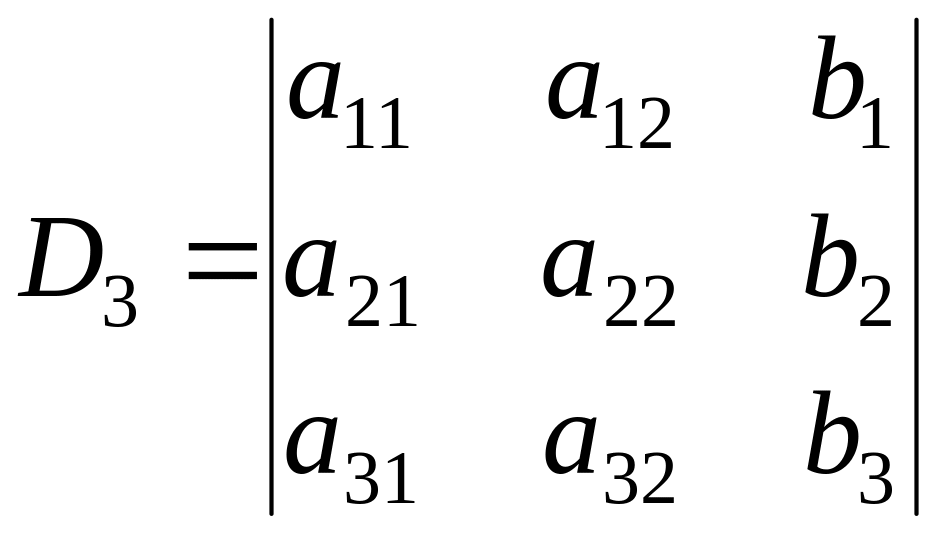Задача 8. Решить систему трех линейных уравнений с тремя неизвестными
.
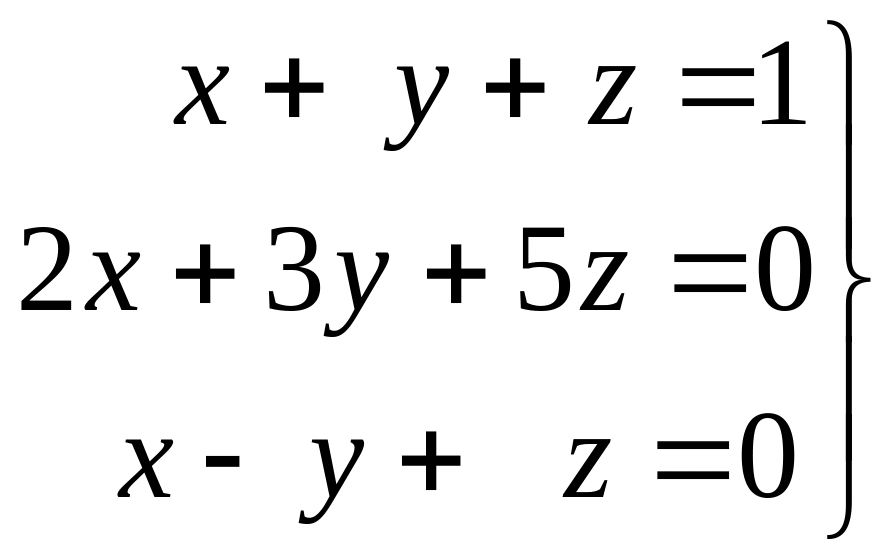Ответ.
.
7. Преобразование декартовых координат на плоскости.
При
параллельном переносе системы координат
вдоль вектора
получаем новую систему
,
где
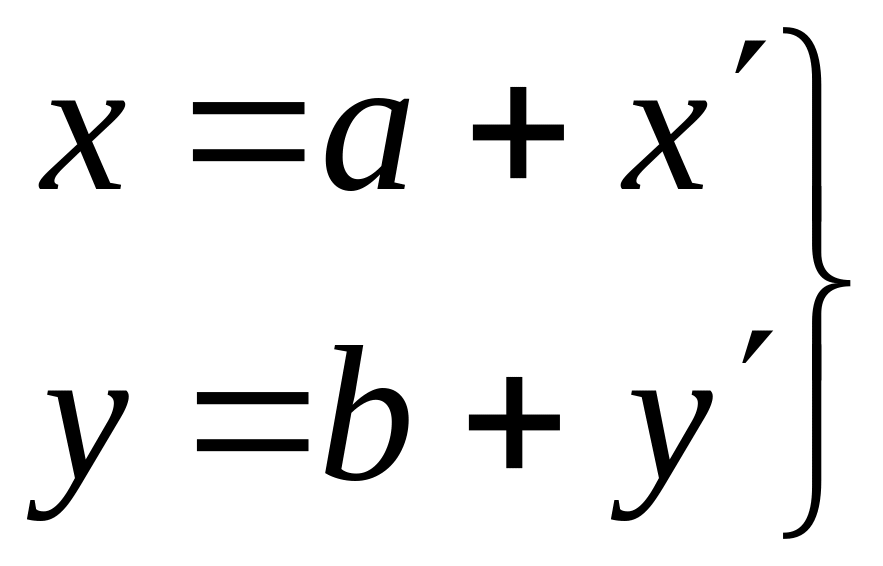. (1.33)
Здесь
– координаты точки
относительно старой системы координат,
– координаты той же точки относительно
новой системы,
– координаты нового начала
относительно старой системы.
Задача
1. Даны
точки
.
Найти их координаты в новой системе,
если начало координат перенесено в
точку
.
Решение. Согласно (1.33) запишем:
.
Следовательно,
для точки
получаем
Координаты
точек
в новой системе найдите самостоятельно.
Ответ.
Задача
2.
Дана функция
.
Найти выражение
этой
функции в новой системе координат, если
начало координат перенесено в точку
.
Решение.
Подставим в функцию
вместо
и
их выражения через новые координаты
и
:
.
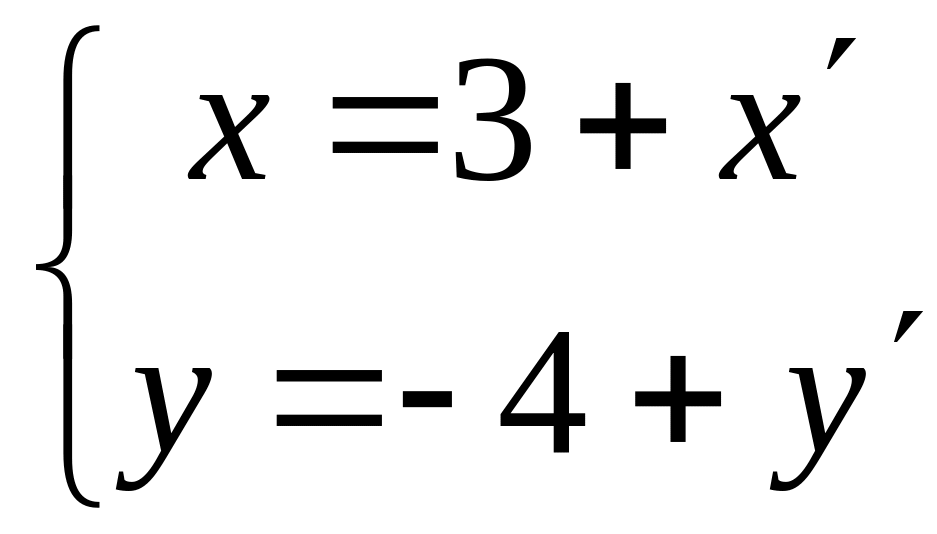Получим
.
В новой системе координат функция принимает вид
.
Вид функции упростился за счет отсутствия членов с первыми степенями новых переменных и .
Задача
3.
Найти точку, при перенесении в которую
начала координат выражение для функции
не содержало бы членов первой степени
относительно новых переменных.
Ответ.
Начало координат нужно перенести в
точку
.
При повороте системы координат на угол (против часовой стрелки) старые координаты произвольной точки связаны с новыми ее координатами соотношениями:
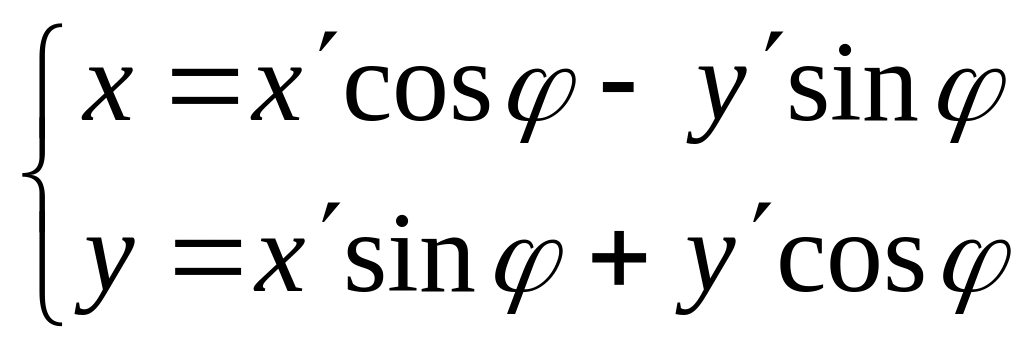1.34)
Задача
4.
Систему координат повернули на угол
.
В новой системе известны координаты
точки
.
Определить координаты этой точки в
старой системе.
Решение. Согласно (1.32) вычислим
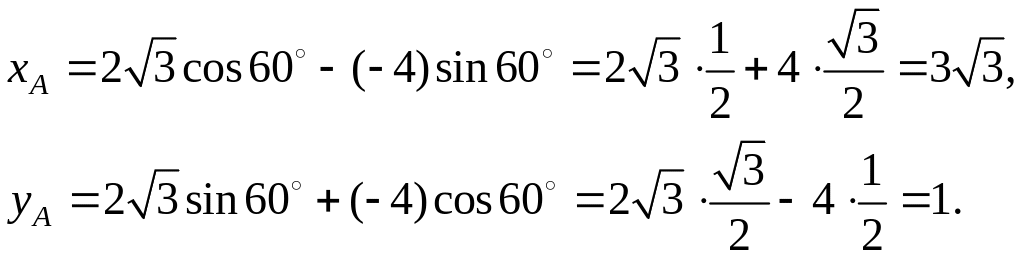
Следовательно,
в старой системе
.
Задача
5.
Дана функция
.
Координатные
оси повернули на угол
.
Найти выражение для этой функции в новой
системе координат.
Решение. Согласно (1.34) находим:
.
В новой системе координат заданная функция вместо квадратов переменных содержит лишь их произведение.
Задача
6.
Доказать, что выражение функции
не изменяется при повороте координатных
осей на произвольный угол
.
Задача
7.
На какой угол нужно повернуть координатные
оси, чтобы выражение функции
после преобразования не содержало члена
с произведением новых переменных?
Решение. Преобразуем выражение данной функции в соответствии с (1.34):
Коэффициент
при произведении
должен равняться нулю:
.
После элементарных преобразований получаем уравнение
,
или
.
Этому
условию удовлетворяют углы
=30, =120; =60; =150;…
Одну
из двух произвольных (правых) декартовых
систем координат можно получить из
другой путем параллельного переноса
на вектор
и последующего поворота на угол
(против часовой стрелки):
(1.35)
Задача
8.
Координаты точек
определены в новой системе координат.
Вычислить координаты этих точек в старой
системе, если начало координат перенесено
в точку
,
а координатные оси повернули на острый
угол
.
Решение.
Найдем сначала
:
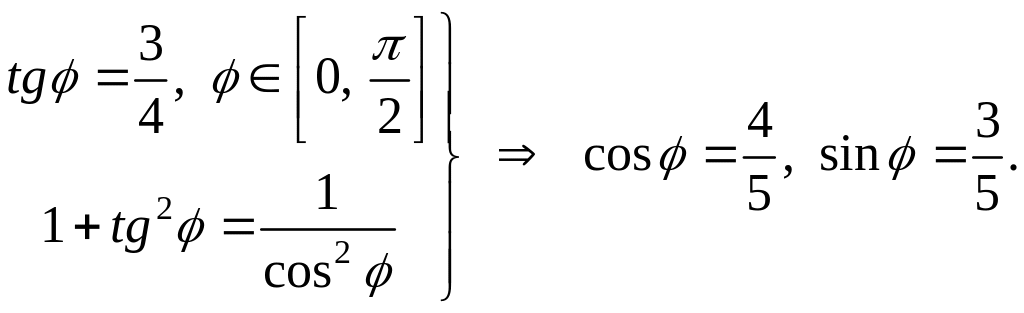
Теперь по формулам (1.35) для старых координат точки получаем:
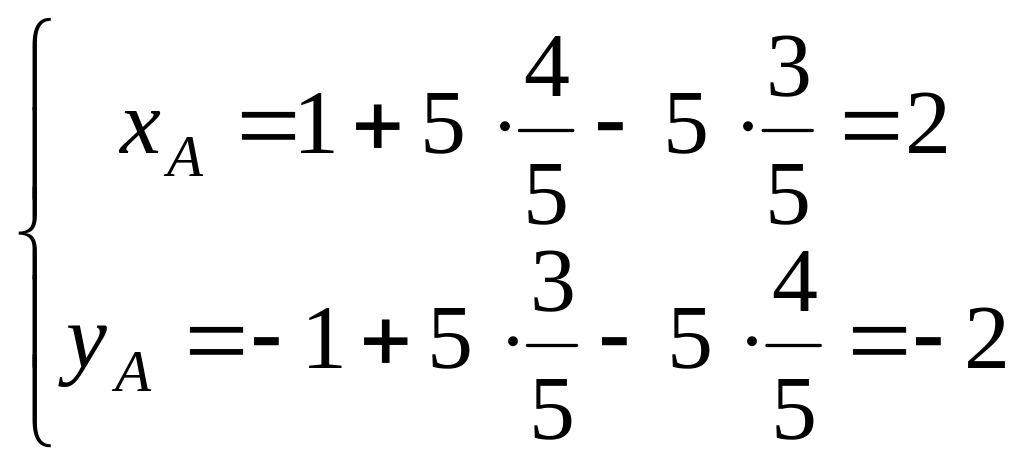
Старые координаты точки определите самостоятельно.