
- •Содержание
- •1. Векторная алгебра
- •1.1. Понятие вектора. Линейные операции над векторами.
- •1.2. Линейная зависимость и независимость векторов. Понятие базиса.
- •1.3. Скалярное произведение. Условие ортогональности двух векторов.
- •1.4. Векторное произведение.
- •5. Смешанное произведение. Условие компланарности трех векторов. Двойное векторное произведение.
- •6. Определители второго и третьего порядка. Системы линейных уравнений
- •1) По первой строке, 2)по второму столбцу.
- •7. Преобразование декартовых координат на плоскости.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
Марковская Е.В., Колесник В.И., Сорока В.А., Сулим Т.П.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ЗАДАЧАХ
Учебно-методическое пособие
Донецк 2011
УДК 516.0
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ЗАДАЧАХ (учебно-методическое пособие для студентов всех специальностей физико-технического факультета) / Донецк, ДонНу, 2011 год. Стр.91.
Марковская Елена Васильевна,
Колесник Валентина Ивановна,
Сорока Владимир Андреевич,
Сулим Татьяна Петровна.
Данное пособие представляет первую часть общего курса “Аналитическая геометрия и линейная алгебра”, а именно, раздел “Аналитическая геометрия”. Приведен также вспомогательный материал об определителях второго и третьего порядков и решении систем двух и трех линейных уравнений, а также о преобразовании декартовых координат на плоскости.
Необходимый теоретический материал подается постепенно, сопровождаемый на каждом шагу примерами решения задач. Особое внимание обращается на физическую интерпретацию основных положений. Каждый раздел дополнен подбором задач для самостоятельной работы.
Предназначено для студентов всех специальностей
физического факультета.
Печатается по решению Ученого совета
Физико-технического факультета ДонНу
Содержание
|
1. Векторная алгебра |
Стр. |
1.1 |
Понятие вектора. Линейные операции над векторами |
3 |
1.2 |
Линейная зависимость и независимость векторов. Понятие базиса. |
6 |
1.3 |
Скалярное произведение. Условие ортогональности двух векторов. |
13 |
1.4 |
Векторное произведение. Условие коллинеарности двух векторов. |
18 |
1.5 |
Смешанное произведение. Условие компланарности трех векторов. Двойное векторное произведение |
22 |
1.6 |
Определители второго и третьего порядков. Системы линейных уравнений |
27 |
1.7 |
Преобразование декартовых координат на плоскости. |
32 |
|
2. Прямые и плоскости |
|
2.1 |
Основные формы уравнения прямой на плоскости |
35 |
2.2 |
Основные формы уравнения плоскости. |
51 |
2.3 |
Прямая в пространстве. Взаимное расположение прямой и плоскости. |
56 |
|
3. Линии и поверхности второго порядка |
|
3.1 |
Окружность. |
64 |
3.2 |
Эллипс. Эксцентриситет и директрисы эллипса. |
66 |
3.3 |
Гипербола. Эксцентриситет и директрисы гиперболы. |
75 |
3.4 |
Парабола. |
80 |
3.5 |
Поверхности второго порядка. |
83 |
|
Литература |
91 |
1. Векторная алгебра
1.1. Понятие вектора. Линейные операции над векторами.
В физике встречаются величины скалярные – масса, время, температура, которые характеризуются только числовым значением, и векторные – сила, скорость, ускорение. Векторные величины кроме числового значения имеют определенное направление в пространстве. Геометрически векторные величины изображаются с помощью направленных отрезков – векторов.
Если
начало отрезка находится в точке
![]() ,
а
конец его – в точке
,
а
конец его – в точке
![]() ,
то соответствующий вектор обозначается
символом
,
то соответствующий вектор обозначается
символом
![]() ,
–
точка приложения вектора. Значит, вектор
можно определить как упорядоченную
пару точек, где первая точка – это начало
вектора, вторая – его конец. Длина
(модуль)
вектора
–
это длина
,
–
точка приложения вектора. Значит, вектор
можно определить как упорядоченную
пару точек, где первая точка – это начало
вектора, вторая – его конец. Длина
(модуль)
вектора
–
это длина
![]() направленного отрезка. Вектор, конец
которого совпадает с началом, называем
нулевым,
длина такого вектора равна нулю. Этот
вектор не имеет определенного направления.
Вектор, длина которого равна 1,
называем единичным.
Вектор можно обозначать также сокращенно
символом
а,
его длину обозначают
направленного отрезка. Вектор, конец
которого совпадает с началом, называем
нулевым,
длина такого вектора равна нулю. Этот
вектор не имеет определенного направления.
Вектор, длина которого равна 1,
называем единичным.
Вектор можно обозначать также сокращенно
символом
а,
его длину обозначают
![]() .
Единичный вектор
.
Единичный вектор
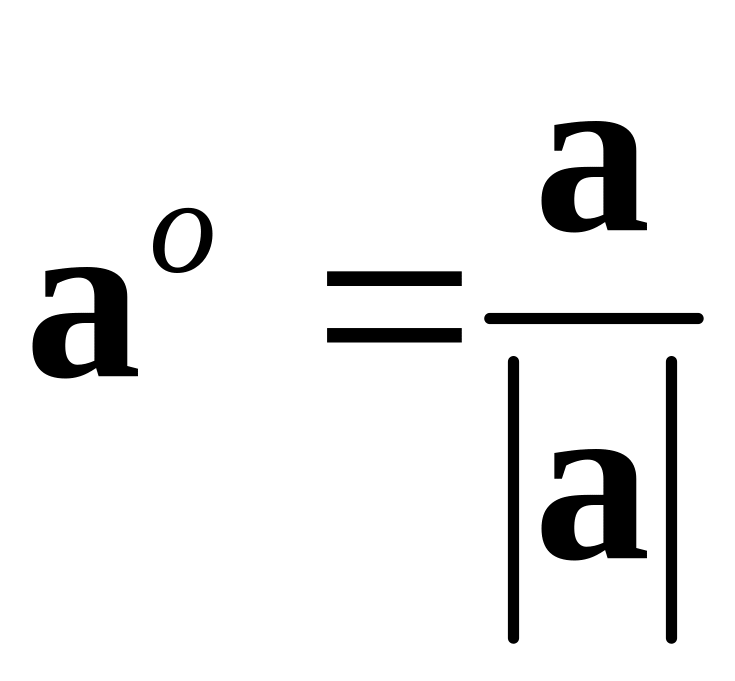 называется ортом
вектора
называется ортом
вектора
![]() .
.
Векторы
а
и
![]() называем коллинеарными,
║
,
если они лежат на одной прямой или на
параллельных прямых.
называем коллинеарными,
║
,
если они лежат на одной прямой или на
параллельных прямых.
Векторы
а
и
равны,
![]() ,
если они
,
если они
1)
коллинеарны:
![]() ,
,
2)
направлены в одну сторону:
![]() ,
,
3)
имеют одинаковую длину:
=![]() .
.
Если
не выполняется хотя бы одно из этих
условий, то
![]() .
Очевидно, все нулевые векторы равны.
.
Очевидно, все нулевые векторы равны.
В математике точку приложения вектора можно выбрать произвольно. Иначе, векторы определяются с точностью до точки приложения (свободные векторы).
Линейными
операциями
называют сложение векторов а,
и умножение вектора а
на
число
![]() .
.
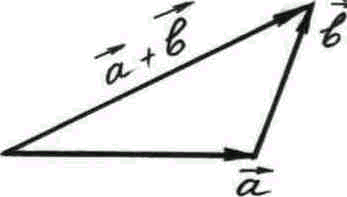
При сложении векторов а и пользуются правилом треугольника: к концу вектора а прилагают начало вектора , тогда вектор суммы а+ идет из начала вектора а в конец вектора . Можно складывать векторы по правилу параллелограмма: векторы а и прилагают к общему началу, тогда вектор суммы а+ совпадает с диагональю параллелограмма, построенного на векторах а и (рис. 1).

З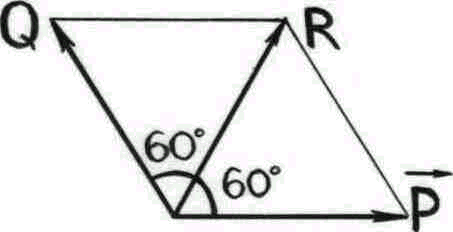 адача
1.
К одной точке приложены две силы
адача
1.
К одной точке приложены две силы
![]() и
и
![]() ,
которые действуют под углом
,
которые действуют под углом
![]() ,
|
|=|
|=7кг.
Найти величину равнодействующей
,
|
|=|
|=7кг.
Найти величину равнодействующей
![]() данных сил (рис. 2).
данных сил (рис. 2).
Решение. Складывая равные по величине силы
Рис.2
и
по
правилу параллелограмма,
получаем,
что их 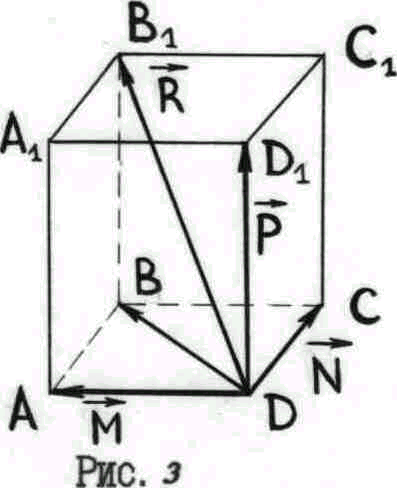 равнодействующая
равнодействующая
![]() направлена по диагонали ромба, поэтому
делит угол между силами пополам. Значит,
величина равнодействующей |
|=7кг
как сторона равностороннего треугольника.
направлена по диагонали ромба, поэтому
делит угол между силами пополам. Значит,
величина равнодействующей |
|=7кг
как сторона равностороннего треугольника.
Задача
2.
Три силы
![]() и
приложены к одной точке и имеют взаимно
перпендикулярные направления. Вычислить
величину их равнодействующей
и выразить вектор
через
векторы
и
,
если известно
и
приложены к одной точке и имеют взаимно
перпендикулярные направления. Вычислить
величину их равнодействующей
и выразить вектор
через
векторы
и
,
если известно
![]()
![]() .
.
Решение.
Пусть силы приложены к точке
![]() (рис.3). Тогда
(рис.3). Тогда
![]() По правилу параллелограмма
По правилу параллелограмма
![]() ,
,
![]()
![]() .
Осталось
найти
диагональ параллелепипеда, построенного
на векторах
и
:
.
Осталось
найти
диагональ параллелепипеда, построенного
на векторах
и
:
![]()
![]() .
.
Правило
параллелограмма дает и разность
векторов
а![]() –
это диагональ, которая идет из конца
вектора
в конец вектора а.
По правилу треугольника легко проверяем
(см. рис.1):
–
это диагональ, которая идет из конца
вектора
в конец вектора а.
По правилу треугольника легко проверяем
(см. рис.1):
![]() .
.
Сумму нескольких векторов удобно находить по правилу многоугольника: к концу предыдущего слагаемого прилагают начало следующего, тогда сумма векторов идет из начала первого в конец последнего слагаемого. Этим правилом часто пользуются в механике при определении равнодействующей нескольких сил.
Компланарными называем векторы, которые расположены в одной плоскости или в параллельных плоскостях.
З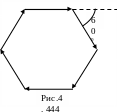 адача
3. Найти
равнодействующую шести равных по
величине компланарных сил, если угол
между двумя последовательными силами
равен
адача
3. Найти
равнодействующую шести равных по
величине компланарных сил, если угол
между двумя последовательными силами
равен
![]() .
.
Решение. Складывая векторы по правилу многоугольника, получаем (рис. 4) замкнутый шестиугольник. Значит, равнодействующая данных сил равна нулю.
Задача 4. Найти равнодействующую пяти компланарных сил, равных по величине, если угол между двумя последовательными силами равен 108˚.
Ответ. Равнодействующая равна 0.
При
умножении вектора
на число
![]() получаем вектор
получаем вектор
![]() ,
который
,
который
1)
![]() ;
;
2)
![]() ,
если
,
если
![]() ,
,
![]() ,
если
,
если
![]() ;
;
3)
![]() .
.
Геометрический
смысл этой операции – "растяжение"
вектора
в
раз. Собственно, при
![]() –
растяжение, при
–
растяжение, при
![]() – сжатие, а при
–
изменение направления с растяжением
или сжатием в зависимости от величины
– сжатие, а при
–
изменение направления с растяжением
или сжатием в зависимости от величины
![]() .
.
Значит,
пропорциональные векторы а
и
коллинеарны. Верно и обратное: если
векторы а
и
коллинеарны, то они пропорциональны,
то есть существует такое число
,
что
![]() (при условии
(при условии
![]() ).
).
При
умножении произвольного вектора
на число 0 получаем нулевой вектор, при
умножении
![]() -вектора
на произвольное число
также получаем
-вектор.
-вектора
на произвольное число
также получаем
-вектор.
Задача 5. С помощью параллелограмма, построенного на векторах а и , проверьте на рисунке справедливость тождеств:
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
,
4)
![]() ,
5)
,
5)
![]() .
.
Задача
6. Может
ли вектор
![]() быть направленным по биссектрисе угла
между слагаемыми
и
?
быть направленным по биссектрисе угла
между слагаемыми
и
?
