6 Карты и планы, используемые при создании документации кадастра объектов недвижимости

В Федеральном законе РФ «О государственной регистрации прав на недвижимое имущество и сделок с ним» (ст. 12, п. 6) в ка­честве объектов недвижимости названы: земельные участки, зда­ния, сооружения, помещения, квартиры, а также иные объекты недвижимого имущества, прочно связанные с земельным участ­ком; иные объекты, входящие в состав зданий и сооружений. Гео­дезические, картографические и другие данные необходимы для того, чтобы достоверно определить месторасположение границы объекта недвижимости, его площадь, а также качественные харак­теристики почв, растительности, несущей способности грунтов и др.

При создании документации кадастра объекта недвижимости можно использовать различные картографические материалы, представленные в виде: топографических карт и планов; планов (карт) границ земельного участка; карт (планов) земельного участ­ка; кадастровых планов земельных участков; дежурных кадастро­вых карт; цифровых моделей местности; электронных карт (пла­нов).

Далее описаны эти карты (планы), дан анализ их содержания и приведены характеристики точности топографических карт.

Точность геодезических данных, полученных при межевании земельных участков

В соответствии с действующими «Требованиями к оформле­нию документов о межевании, предъявляемых для постановки зе­мельных участков на государственный кадастровый учет» при оформлении разделов «Описание границ» и «Сведения о земель­ных участках» необходимы следующие геодезические данные:

1 – плоские прямоугольные координаты межевых знаков, уста­новленных в поворотных точках границы объекта землеустрой­ства;

2 – горизонтальные проложения и дирекционные углы (геоданные) между смежными межевыми знаками;

3 – уточненная, по данным натурных измерений, площадь зе­мельного участка.

Геодезические данные, перечисленные в пунктах 2 и 3, обычно соответствуют функциям координат межевых знаков, численные значения которых, как отмечалось ранее, могут быть получены различными способами. Так как геодезические и картометрические действия при отсутствии систематических со­провождаются случайными погрешностями измерений, то точно­сти функций координат межевых знаков можно оценить на основе правил теории погрешностей измерений. Приведем основное из них. Рассмотрим некоторую функцию F, состоящую из и незави­симых переменных (аргументов) х₁, х₂, ..., х_n„, которую представим в общем виде

F=f(x_hx₂,...,x_n) (1)

Дисперсия этой функции имеет вид

(2)

где – частные производные функции от аргументов; m_хi – средние квадратические погрешности независимых аргументов (i = 1,2, ..., и).

Средняя квадратическая погрешность m_F функции может быть найдена путем извлечения квадратного корня из обеих час­тей равенства (2) , т.е.

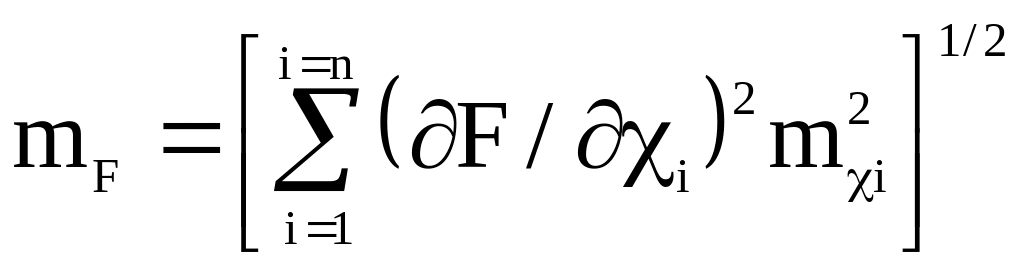(3)

По формуле (3) оценивают достоверность геодезических дан­ных, учитываемых при оформлении документов о межевании объектов землеустройства.

Точность плоских прямоугольных координат межевых знаков.

Точность плоских прямоугольных координат межевых знаков характеризуется их средними квадратическими погрешностями т_х и т_у, относящимися соответственно к осям абсцисс и ординат де­картовой системы координат. Численные значения этих погреш­ностей можно найти по данным уравнительных вычислений ме­жевой съемочной сети, используя ПЭВМ и соответствующее про­граммное обеспечение. Вместе с тем при априорных расчетах точ­ности погрешностей координат, т. е. независимо от конкретных результатов уравнительных вычислений, значения т_х и т_у могут быть получены при использовании данных, приведенных в табли­це 1 следующим образом.

Средняя квадратическая погрешность положения межевого знака

(4)

При круговом рассеивании погрешностей координат можно считать, что средние квадратические погрешности их абсцисс и ординат будут равны между собой, т. е. т_х = т_у. Тогда

(5)

По формуле (5) вычислим погрешности т_х\у для различных градаций земель, которые приведены в таблице1. Средние квад­ратические погрешности М_с из таблицы 1 примем равными по­грешностям М_t. Результаты вычислений в таблице 1:

Номер градации земель	1	2	3	4	5
тх/у, м	0,07	0,14	0,35	1,8	3,6

Значения средних квадратических погрешностей, приведенные в таблице 1, характеризуют точность координат межевых знаков, центры которых обозна-чены гвоздями, вбитыми в торцы деревян­ных столбов, или насечками, нанесе-ными на металлические стержни и другие аналогичные предметы. Если обозна-чения цент­ров межевых знаков отсутствуют, то однозначно идентифициро­вать их положение невозможно. В этом случае среднюю квадратическую погреш-ность М,' положения межевого знака можно пред­ставить в виде приближенного равенства

где d – размер диагонали торца межевого знака в виде прямоугольника или диа­метра его окружности.

На землях поселений отсутствие обозначения центра межевого знака при d≤ 5 см практически не влияет на достоверность иден­тификации его местоположения. Вместе с тем, при дальнейшем использовании межевого знака в качестве исходного геодезичес­кого пункта для инструментальной съемки недвижимости, восста­новления границы земельного участка и т. п. обозначение его цен­тра является обязательным условием производства геодезических работ.

При проведении территориального землеустройства с целью получения сведений о земельном участке как объекте налогообло­жения может быть использован картографический материал, чис­ленный масштаб которого позволяет идентифицировать местопо­ложение границы земельного участка. Надежность такой иденти­фикации в значительной степени зависит от точности определе­ния местоположения межевых знаков, координаты которых могут быть получены на основе соответствующих картометрических из­мерений по топографическим картам (планам) и другим картогра­фическим материалам масштабов от 1 : 500 до 1 : 10000 и мельче. Значения средних квадратических погрешностей положения контурных точек на плане, с по­мощью которых можно идентифицировать местоположение пово­ротных точек границы объекта землеустройства, не постоянны, т. е. определяются топографическими условиями местности и дру­гими факторами. С учетом сказанного, можно принять среднюю квадратическую погрешность М_t положения межевого знака рав­ной средней квадратической погрешности m_t положения контур­ной точки на плане. По формуле (5) вычислим средние квадратические погрешности m_х\у координат межевых знаков для некото­рых градаций земель (см. табл.1), приняв при этом во внимание значения погрешностей т_t положения контурных точек на плане

Номера градаций земель	1	2	4
Mх\у, мм	0,22	0,36	0,50

В целях идентификации местоположения границ земельного участка в городах обычно используют планы (карты) масштабов 1 : 500 – 1 : 1000, а на землях сельских поселений – 1 : 2000 – 1 : 5000. Поэтому в условиях городской застройки средняя квадратическая погрешность межевого знака в зависимости от масштаба планово-картографической основы может изменять­ся от 0,15 до 0,30 м, а на территории сельских поселений – 1,0...2,5 м. При проведении территориального землеустройства на землях сельскохозяйственного назначения обычно используют карты масштаба 1 :10000. В этом случае средняя квадратическая погрешность положения межевого знака составит не менее 7 м. В качестве предельной погрешности ∆t положения межевого знака примем величину, равную .

Точность изображения расстояний с использованием координат межевых знаков

Проанализируем точность определения горизонтального рас­стояния S, вычисленного по координатам его концевых точек. Из решения обратной геодезической задачи это расстояние можно вычислить по формуле

(6)

где х₁ и х₂; у₁ и у₂ – соответственно абсциссы и ординаты концов линии.

Примем, что средние квадратические погрешности абсцисс и ординат межевых знаков 1 и 2 соответственно имеют значения m_xi и m_yi, (i= 1,2). По формуле (2) найдем дисперсию этого расстоя­ния

(7)

где и – частные производные функции по соответствующим независимым аргументам.

Найдем значения частных производных:

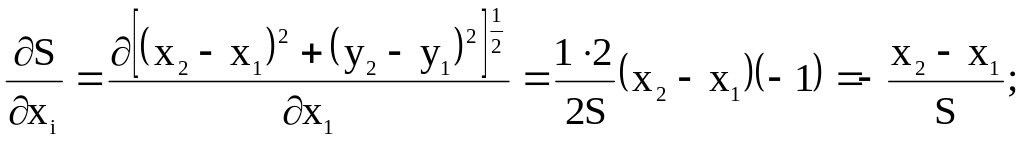
Подставив найденные значения частных производных в фор­мулу (7) , получим

(8)

Как уже было отмечено, при круговом рассеивании погреш­ностей абсцисс и ординат по формуле (5) можно принять, что их средние квадратические погрешности будут равны между собой, т.е.

m_xi=m_yi=M_ti/ ,

где М_ti – средняя квадратическая погрешность положения i-го межевого знака.

После несложных преобразований получим

(9)

Нетрудно заметить, что выражения, стоящие в квадратных скобках в уравнении (9), равны S². Поэтому выражение (9) можно преобразовать и записать его в следующем виде

(10)

Из формулы (10) следует, что дисперсия расстояния равна полусумме дисперсий положения конечных межевых знаков Если принять, что средние квадратические погрешности положения межевых знаков 1 и 2 равны между собой, т. е. предположить, что M_t1= М_t2 = M_t, то по формуле (10) получим

m_s = M_t, (11)

Согласно выражению (11) можно сделать следующий вывод. Если средние квадратические погрешности положения межевых знаков равны между собой, то средняя квадратическая погреш­ность расстояния между ними равна средней квадратической по­грешности положения одного из них.

С учетом формулы (5) формулу (11) можно представить в следующем виде:

m_s=m_xly . (12)

По формуле (11) можно априори рассчитать средние квадра­тические погрешности горизонтальных расстояний между меже­выми знаками для различных градаций земель/ Заметим, что при опреде­лении координат межевых знаков полярным способом с одного пункта межевой съемочной сети для расчета погрешности m_s от­носительно этого пункта МСС следует воспользоваться формулой (11) и соответствующими значениями квадратических погреш­ностей (см. табл. 1), приняв M_t = М₃. При определении расстоя­ний по координатам межевых знаков, полученным измерением по картам (планам) различных масштабов, среднюю квадратическую погрешность m_s (м на местности) можно вычислить по формуле (12), приведя ее к виду

m_s =т_х/у(мм)Т 10 ^-3 , м

где Т – знаменатель численного масштаба карты (плана).

При этом используют значения погрешностей координат ме­жевых знаков.

Точность изображения направлений линий

Направление линии на плоскости можно определить из реше­ния обратной геодезической задачи по формуле

(13)

где α – дирекционный угол направления с межевого знака 1 на межевой знак 2;

х₁,х₂;у₁,у₂ – соответственно абсциссы и ординаты межевых знаков 1 и 2.

Примем как в предыдущем разделе средние квадратические погрешности положения межевых знаков 1 и 2 соответственно равными М_n и Ma.

Продифференцируем выражение (13) по независимым пере­менным – абсциссам и ординатам межевых знаков 1 и 2. В резуль­тате получим

Перейдем от дифференциалов к средним квадратическим по­грешностям. После приведения подобных членов и несложных преобразований будем иметь

(14)

Согласно формулы (5) примем, что т_ti = m_yi =M_ti \ и пере­пишем форму-лу (14) в следующем виде

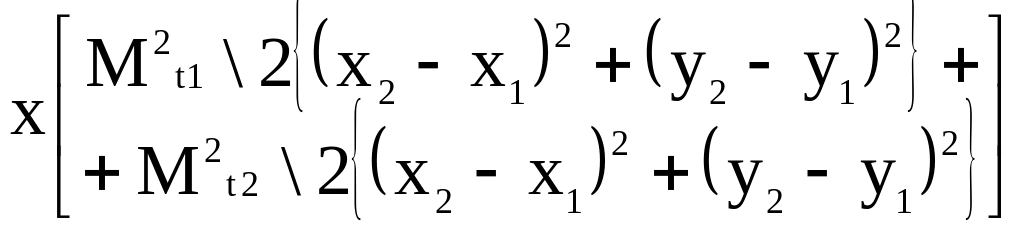
В этом равенстве выражения, стоящие в фигурных скобках, со­гласно формуле (6) равны S². Так как

то дисперсия дирекционного угла

Такие проекции особенно удобные для определения направления и

(15)

При равенстве средних квадратических погрешностей положе­ния 1-го и 2-го межевых знаков, т. е. когда М_t1 = М_t2 = М_t, формула (15) примет простой вид

(16)

или

(17)

где ρ = 3438'.

Из последнего равенства следует, что средняя квадратическая погрешность дирекционного угла увеличивается с уменьшением расстояния между межевыми знаками. Например, если принять M_е= 0,1 м и S= 60 м, то по формуле (16) получим

т_а = 0,1*3438/60 = 6'.

Наиболее значимую погрешность имеют направления, рассчи­танные по координатам межевых знаков, полученным измерения­ми по картам (планам). Например, если земельный участок распо­ложен на городских землях, то можно принять т_x/y = 0,22 мм . Подставив значение этой погрешности в формулу (17) и приняв S=60 мм, найдем: т_а =0,22*3438 /60 = 18'. Предельная погрешность Δα = 2т_а, и в данном примере Δα = 40'.

Точность определения площади земельного участка по координатам межевых знаков

Площадь земельного участка, которую отражают на плане гра­ниц объекта землеустройства или на плане объекта землеустрой­ства, вычисляют по плоским прямоугольным координатам пово­ротных точек границы земельного участка, закрепленных на мест­ности межевыми знаками, по формуле

(18)

где x_i и y_i – соответственно абсциссы и ординаты межевых знаков (i= 1,2,..., п), полученные в результате межевания объекта землеустройства.

Обозначим, как и прежде, средние квадратические погрешнос­ти поло-жения межевых знаков как М_t1, а средние квадратические погрешности их координат – m_xi/yi. На основании формулы (2), и приняв во внимание выраже-ние (18), запишем

(19)

где т_P – средняя квадратическая погрешность площади земельного участка;

и – частные производные функции (7.18) соответственно по независимым переменным х_i и y_i .

Найдем значения частных производных:

(20)

(21)

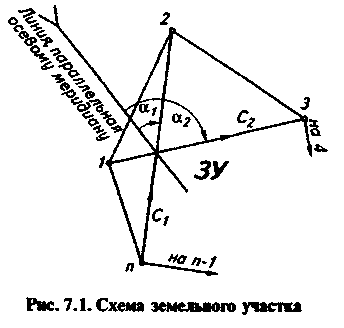
где C_i и α_i – соответственно диагональ, противолежащая межевому знаку с номером i, и ее дирекционный угол в направлении от межевого знака с номером i – 1 к межевому знаку с номером i+ 1 (рис. 7.1).

Подставив найденные значения частных производных (20) и (21) в формулу (19), найдем

(22)

Принимая во внимание формулу (5), т.е. полагая, что m_xi = m_yi = M_ti / , уравнение (22) после простых преобразований приведем к виду:

(23)

Так как cos²α_i + sin²α_i = 1, то формулу (23) с учетом сказанного запишем в следующем виде

(24)

В частном случае, когда средние квадратические погрешности положения межевых знаков равны между собой, т. е. M_t1 = M_t2 = ...M_tn = М_t из формулы (24) следует, что

(25)

Полученное выражение можно использовать для оценки точности опре-деления площади земельного участка, вычислив соответствующие диагонали с_i, а также приняв во внимание значение средней квадратической погрешности М_i, положения межевого знака для определенной градации земель. При предварительных расчетах точности площади объектов землеустройства можно воспользоваться некоторыми типовыми геометрическими фигурами. Например, земельный участок в виде прямоугольника или квадрата, площади которых вы­числены по плоским прямоугольным координатам поворотных точек (ме­жевых знаков) 1, 2, 3 и 4 по формуле (18).

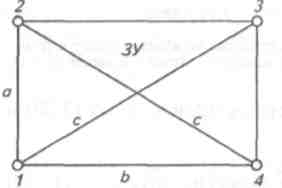
Р ис – Земельный участок прямоугольной формы

Для земельного участка в виде прямоугольника каждая из его четырех диагоналей равна Подставив это значение в формулу (25), получим

или

(26)

Обозначим через К коэффициент К = а/b. Выразим площадь прямо-угольного земельного участка в виде произведения Р = аЬ и заметим, что зна-чение этой же площади Р = b² К. С учетом сделан­ных обозначений из формулы (26) следует, что

Так как b² = Р/К, то окончательно запишем, что средняя квадратическая погрешность площади земельного участка, имеющего вид прямоугольника

(27)

В формуле (27) коэффициент К, равный отношению сторон прямоугольника, численно характеризует их вытянутость. При К = 1 имеем земельный участок в форме квадрата. Как следует из формулы (27), средняя квадратическая погрешность его площа­ди

(28)

Формулы (27) и (28) широко применяют в предварительных расчетах точности определения площади земельного участка по плоским прямоугольным координатам его поворотных точек, ми­нуя вычисления по формуле (25). Для земельного участка произ­вольной конфигурации по ним возможно получить приближенное, с погрешностью 10... 15 %, значение средней квадратической погрешности определения площади земельного участка.

Как было отмечено при территориальном земле­устройстве можно использовать топографические карты, а пло­щадь земельного участка вычислять по плоским прямоугольным координатам, полученным в результате измерения картометрическим способом. Чтобы оценить точность определения площади, га, объекта землеустройства, пользуются формулой:

(29)

в которой площадь Р земельного участка выражена в гектарах; средняя квадратическая погрешность m _х/у координат поворот­ной точки границы земельного участка (межевого знака) – в миллиметрах на плане; средняя квадратическая погрешность пло­щади земельного участка – в гектарах; Т— знаменатель численно­го масштаба карты (плана).

Аналогично можно преобразовать формулу (28). В результате получим

(30)

Рассмотрим примеры использования полученных формул при расчетах точности определения площадей земельных участков. Эти формулы можно использовать для непосредственного опре­деления погрешностей m_p по заданным значениям погрешностей координат, значению площади земельного участка и другим дан­ным, а также с учетом градаций земель, на которых он располо­жен. Далее приведены типовые примеры решения задач.

Задача 1. Оценить точность площади земельного участка, вычисленную по формуле (18), в виде прямоугольника с коэффициентом вытянутости К = 0,5 и площадью Р = 2500 м². Земельный участок расположен в черте городской заст­ройки.

Решение. В соответствии с данными, примем M_t = 0,1 м. Подставив в формулу (27) эти данные и приведенные в условиях к задаче, получим

Учитывая результаты вычислений, значение площади земельного участка сле­довало бы записать в соответствующем месте кадастрового плана земельного учас­тка в таком виде: Р= 2500 ± 6 м².

Задача 2. Оценить точность площади земельного участка, близкого по конфи­гурации к квадрату, равной Р= 100 га, если поворотные точки его границы иден­тифицированы с контурными точками, отображенными на карте масштаба 1:10000. Земельный участок расположен на сельскохозяйственных землях.

Решение. В соответствии с данными, примем m_x/y = 0,5 мм на плане. Подставив в формулу (30) соответствующие исходные дан­ные, получим

С учетом этого результата окончательно можно записать, что Р= 100 ±0,7 га. Следует также иметь в виду, что предельная погрешность ΔР площади с вероятно­стью, близкой к 95 %, составит ∆Р= 2т_Р, т. е. ΔР= 1,4 га.

Точность определения площади объекта недвижимости по данным наружного обмера

Площади земель­ных участков, занятых объектами недвижимости, можно опреде­лить двумя способами: по плоским прямоугольным координатам угловых точек зданий (сооружений), по данным наружных обме­ров.

Для первого, из перечисленных ранее, способа оценить точ­ность определения площади земельного участка, занятого объек­том недвижимости, можно по формулам (25), (27) или (28). При определении площади по данным наружных обмеров прини­мают во внимание, что преобладающее большинство зданий име­ют прямоугольное очертание, т. е. все его углы являются прямы­ми. Площадь здания

P = ab, (31)

где а и b – стороны прямоугольника (рис. 7.2).

Так как стороны а и b получены в результате наружных обме­ров, то им присущи соответствующие погрешности измерений. В соответствии с форму-лами (3) и (31)

т²_р = а²т²_ь+ b²m²_a, (32)

где т_а и т_ь – средние квадратические погрешности соответствующих сторон пря­моугольника.

Обозначим, как и прежде, через коэффициент К отношение а/Ь. Приняв во внимание это отношение, а также формулы (31) и (32), после несложных преобразований найдем

m²_p=b² (K² m²_b + m²_a). (33)

Примем, что стороны прямоугольника измерены со средними квадратическими погрешностями m_s, т. е. m_s=m_a= т_ь. Тогда с учетом этого равенства погрешностей, а также приняв b² = Р/К, формулу (33) представим в виде

(34)

Из формулы (34) следует, что при К= 1, т.е. когда здание имеет форму квадрата, средняя квадратическая погрешность пло­щади земельного участка

(35)

Пример. Вычислить среднюю квадратическую пофешность площади здания прямоугольной формы со сторонами а = 7,05 м и b = 14,03 м при условии, что средняя квадратическая погрешность измерения этих сторон m_s = 0,015 м.

Решение. Вычислим коэффициент К, который составит K= 0,50. Теперь по формуле (34) найдем среднюю квадратическую погрешность площади. Получим

В результате решения задачи получим: Р= 98,9 ± 0,24 м².

Расчеты показывают, что при несложной конфигурации зданий, расположен­ных на земельном участке, площади под постройками следует определять по дан­ным наружных обмеров, а плоские прямоугольные координаты их углов исполь­зовать лишь для нанесения объекта недвижимости на план земельного участка. Это может заметно повысить точность определения площадей земельных участ­ков, занятых объектами недвижимости, при условии, что они имеют строго пря­моугольную форму. При сложной конфигурации здания (сооружения) площадь его лучше определять по плоским прямоугольным координатам его характерных точек, полученным при геодезической съемке объекта недвижимости.