Дифференциальное исчисление функции одной переменной

Производная функции, ее геометрический и физический смысл.

Определение. Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

у

f(x)

f(x₀ +x) P

f

f(x₀) M

  x

0 x₀ x₀ + x x

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1) (u  v) = u  v

2) (uv) = uv + uv

3) , если v  0

Производные основных элементарных функций.

1)С = 0; 9)

2)(x^m) = mx^m-1; 10)

3) 11)

4) 12)

5) 13)

6) 14)

7) 15)

8) 16)

Производная сложной функции.

Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда

Пример. Найти производные функций

1. .

Сначала преобразуем данную функцию:

2.

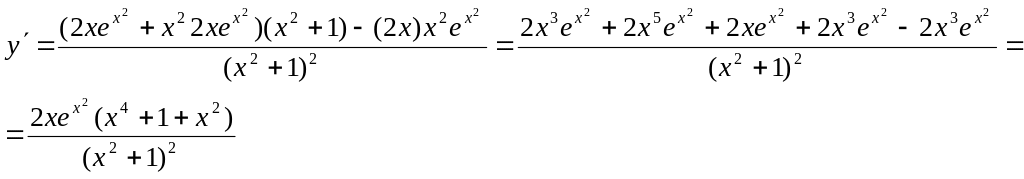
3.

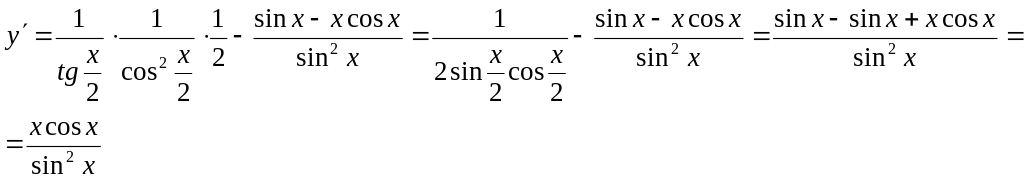
4.

5.

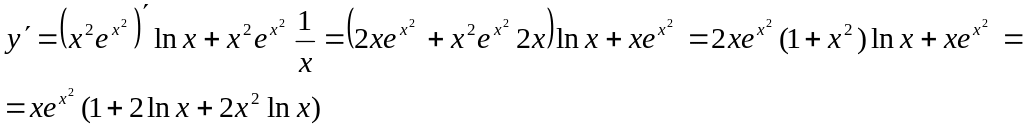
Производные высших порядков.

Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

Если найти производную функции f(x), получим вторую производную функции f(x)

т.е. y = (y) или .

Этот процесс можно продолжить и далее, находя производные степени n.

.

Исследование функций с помощью производной.

Возрастание и убывание функций.

Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f(x)  0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Точки экстремума.

Определение. Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функция f(x) имеет в точке х₂ минимум, если f(x₂ +x) > f(x₂) при любом х (х может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

Определение. Точки максимума и минимума функции называются точками экстремума.

Выпуклость и вогнутость кривой.

Точки перегиба.

Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

у

x

На рисунке показана иллюстрация приведенного выше определения.

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Интегральное исчисление функции одной переменной

Первообразная функция.

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:

F(x) = f(x).

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F₁(x) = F₂(x) + C.

Неопределенный интеграл.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

1.

2.

3.

4. где u, v, w – некоторые функции от х.

1. 

Пример:

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Интеграл		Значение	Интеграл		Значение
1		-lncosx+C	9		ex + C
2		lnsinx+ C	10		sinx + C
3			11		-cosx + C
4			12		tgx + C
5			13		-ctgx + C
6		ln	14		arcsin + C
7			15
8			16

Методы интегрирования.

Рассмотрим три основных метода интегрирования.

Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере:

Требуется найти значение интеграла . На основе известной формулы дифференцирования можно сделать вывод, что искомый интеграл равен , где С – некоторое постоянное число. Однако, с другой стороны . Таким образом, окончательно можно сделать вывод:

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.

Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.

Способ подстановки (замены переменных).

Теорема: Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Пример. Найти неопределенный интеграл .

Сделаем замену t = sinx, dt = cosxdt.

Пример.

Замена Получаем:

Интегрирование по частям.

Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:

или ;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Пример.

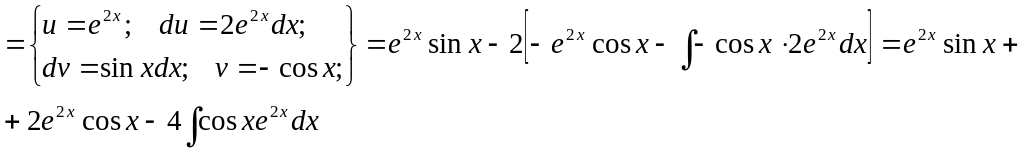
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

Таким образом, интеграл найден вообще без применения таблиц интегралов.

Примеры.

1.

2.

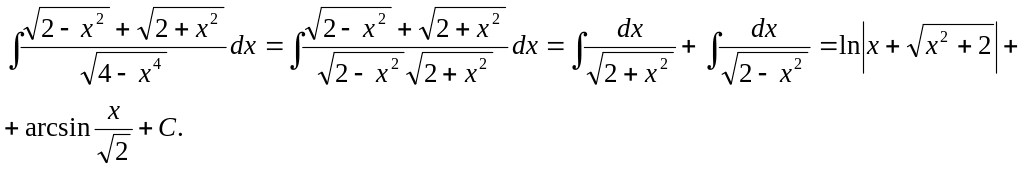
3.

4.

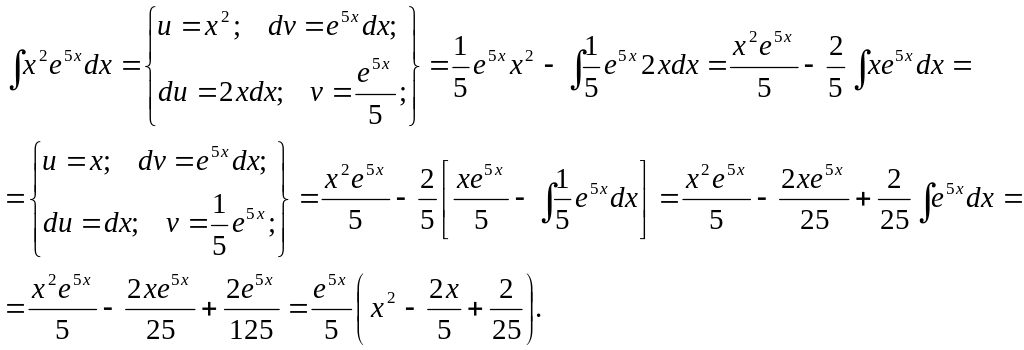
5.

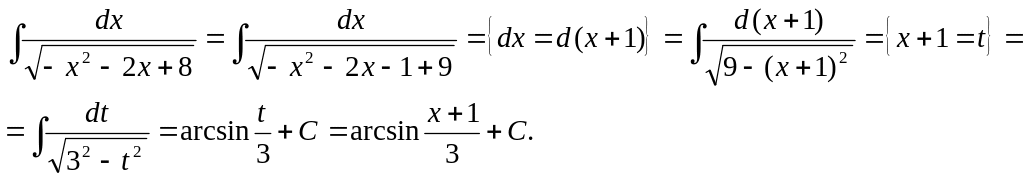
6.

7.

8.

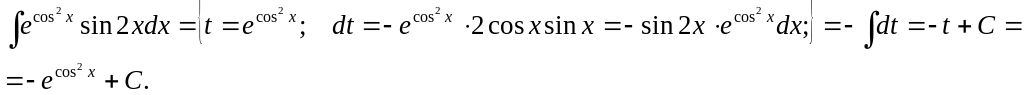
9.

10.

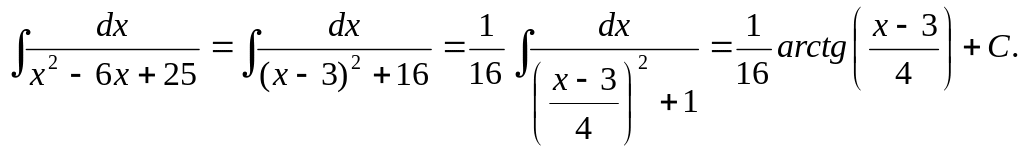
Интегрирование рациональных дробей.

Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.

Теорема: Если - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)^…(x - b)^(x² + px + q)^…(x² + rx + s)^ ), то эта дробь может быть разложена на элементарные по следующей схеме:

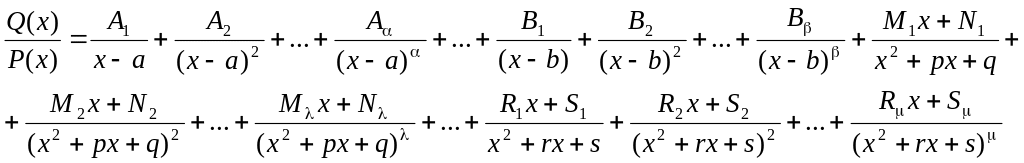
где A_i, B_i, M_i, N_i, R_i, S_i – некоторые постоянные величины.

При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A_i, B_i, M_i, N_i, R_i, S_i применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.

Применение этого метода рассмотрим на конкретном примере.

Пример.

Т.к. ( , то

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

Итого:

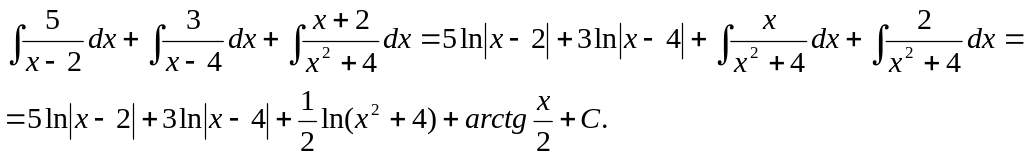
Пример.

Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:

6 x⁵ – 8x⁴ – 25x³ + 20x² – 76x – 7 3x³ – 4x² – 17x + 6

6x⁵ – 8x⁴ – 34x³ + 12x² 2x² + 3

9x³ + 8x² – 76x - 7

9x³ – 12x² – 51x +18

20x² – 25x – 25

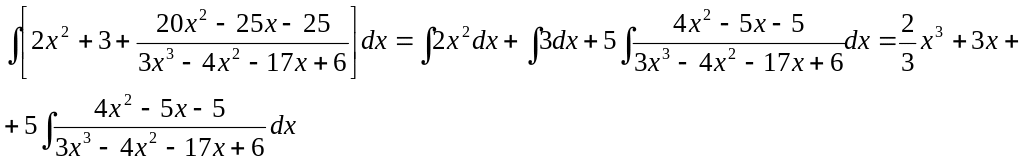
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:

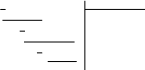3x³ – 4x² – 17x + 6 x - 3

3x³ – 9x² 3x² + 5x - 2

5x² – 17x

5x² – 15x

- 2x + 6

-2x + 6

0

Таким образом 3x³ – 4x² – 17x + 6 = (x – 3)(3x² + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:

Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

Окончательно получаем:

=

Определенный интеграл.

Пусть на отрезке [a, b] задана непрерывная функция f(x).

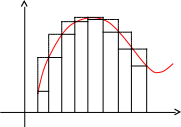y

M

m

0 a x_i b x

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]

Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

x₀ < x₁ < x₂ < … < x_n

Тогда x₁ – x₀ = x₁, x₂ – x₁ = x₂, … ,x_n – x_n-1 = x_n;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

[x₀, x₁]  m₁, M₁; [x₁, x₂]  m₂, M₂; … [x_n-1, x_n]  m_n, M_n.

Составим суммы:

_n = m₁x₁ + m₂x₂ + … +m_nx_n =

_n = M₁x₁ + M₂x₂ + … + M_nx_n =

Сумма называется нижней интегральной суммой, а сумма – верхней интегральной суммой.

Т.к. m_i  M_i, то _n  _n, а m(b – a)  _n  _n  M(b – a)

Внутри каждого отрезка выберем некоторую точку .

x₀ < ₁ < x₁, x₁ <  < x₂, … , x_n-1 <  < x_n.

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].

S_n = f(₁)x₁ + f(₂)x₂ + … + f(_n)x_n =

Тогда можно записать: m_ix_i  f(_i)x_i  M_ix_i

Следовательно,

Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.

Обозначим maxx_i – наибольший отрезок разбиения, а minx_i – наименьший. Если maxx_i 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.

Если , то

Определение: Если при любых разбиениях отрезка [a, b] таких, что maxx_i 0 и произвольном выборе точек _i интегральная сумма стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].

Обозначение :

а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Определение: Если для функции f(x) существует предел то функция называется интегрируемой на отрезке [a, b].

Также верны утверждения:

Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Свойства определенного интеграла.

1. 

2. 

3. 

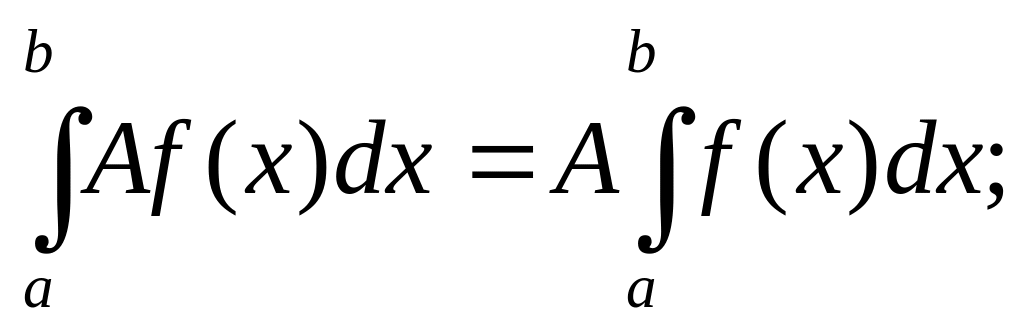
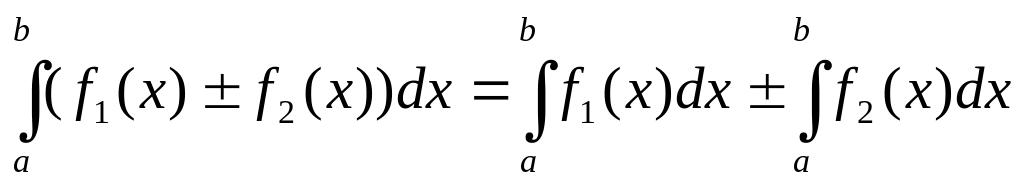
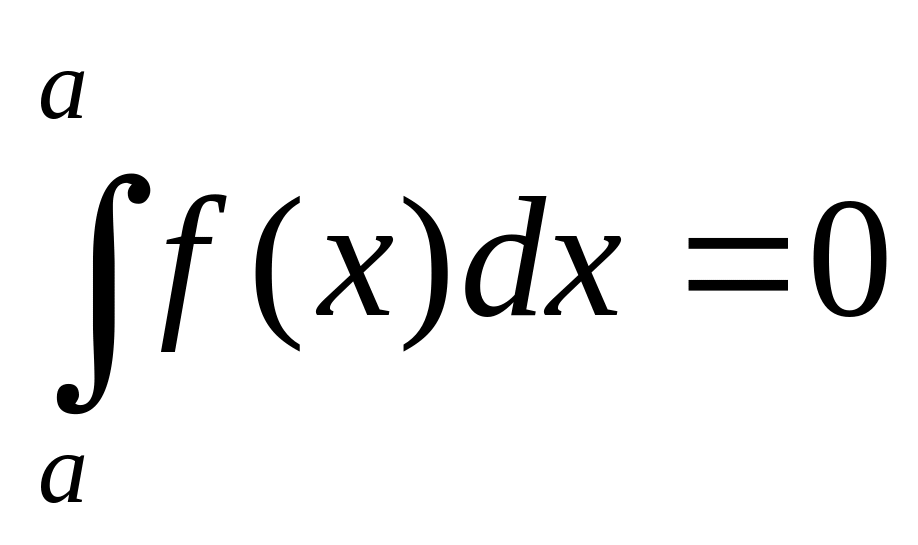
4. Если f(x)  (x) на отрезке [a, b] a < b, то

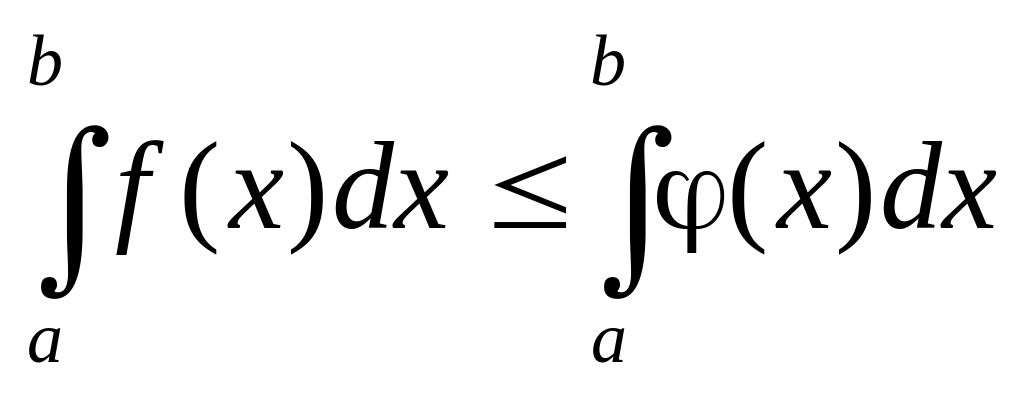
5. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

6. Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка  такая, что

7) Для произвольных чисел a, b, c справедливо равенство:

Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.

8)

Вычисление определенного интеграла.

Теорема: (Теорема Ньютона – Лейбница)

Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то

это выражение известно под названием формулы Ньютона – Лейбница.

Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.

Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.

Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.

Обыкновенные дифференциальные уравнения.

Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.

В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.

Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:

В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.

Тогда получаем: - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).

Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

Пример.

- обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .

- обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается

- дифференциальное уравнение в частных производных первого порядка.

Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Определение. Решение вида у = (х, С₀) называется частным решением дифференциального уравнения.

Определение. Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = (х, С₀), удовлетворяющего начальным условиям у(х₀) = у₀.

Определение. Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

Пример. Найти общее решение дифференциального уравнения .

Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

Теперь интегрируем:

- это общее решение исходного дифференциального уравнения.

Допустим, заданы некоторые начальные условия: x₀ = 1; y₀ = 2, тогда имеем

При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши) .

Пример. Найти общее решение дифференциального уравнения:

Дифференциальные уравнения первого порядка.

Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:

Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.

Преобразуем такое выражение далее:

Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:

• это так называемая дифференциальная форма уравнения первого порядка.

Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.

Уравнения вида y’ = f(x).

Пусть функция f(x) – определена и непрерывна на некотором интервале

a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х₀ и у₀, то можно определить постоянную С.