3.2. Процесс равновесного открытого испарения

Рассмотрим некоторый процесс, мгновенная скорость которого, характеризуемая изменением состава многокомпонентной смеси, соответствует направлению и длине ноды жидкость-пар. Такой процесс может выступать в качестве характеристики диаграммы фазового равновесия и отражать все особенности фазового равновесия.

Перечисленным выше требованиям удовлетворяет процесс равновесной открытой дистилляции, уравнение которого имеет вид в координатной форме:

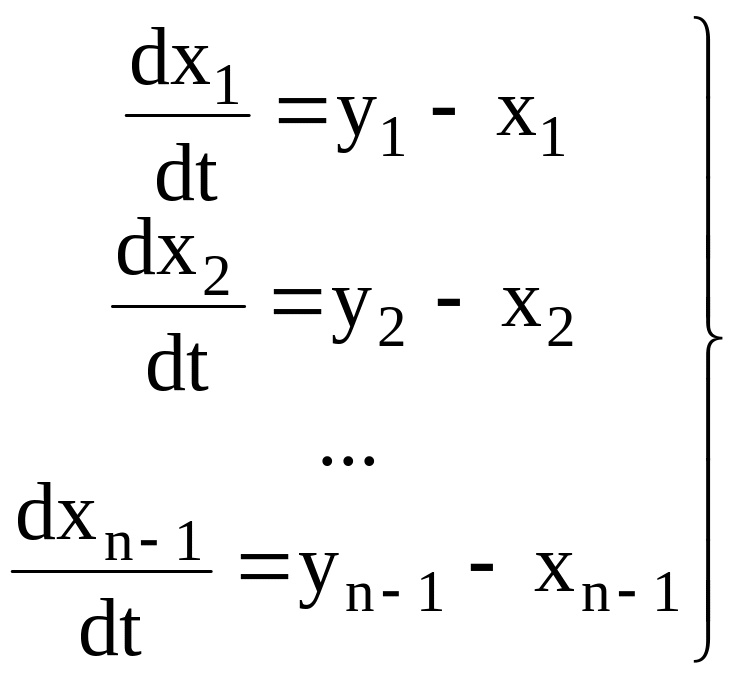(3.7)

и в векторной форме:

dХ/dt = y - x , (3.8)

dt = d ln m ,

где m — количество молей жидкой фазы в перегонной колбе; dХ - изменение состава <dx₁, dx₂, dx₃ ... dx_n> жидкой фазы; Y-X - нода жидкость-пар. Необходимо отметить особо, что в рассматриваемом процессе условное время dt меньше нуля, поскольку при испарении количество жидкости в кубе уменьшается. Таким образом векторы dХ и Y-X колинеарны и разнонаправленны.

Согласно уравнению (3.8), если dХ/dt =0, то Y=X и реализуется особая точка векторного поля нод.

Интегральные линии дифференциального уравнения дистилляции называются траекториями дистилляции (дистилляционными линиями или линиями равновесного открытого испарения) . Эти траектории в окрестности особой точки имеют своеобразный ход.

Определим общие закономерности векторного поля нод.

Для этого необходимо провести операцию линеаризации системы нелинейных дифференциальных уравнений (3.7) и определить типы особых точек.

Запишем уравнения (3.7) через коэффициенты распределения компонентов

(3.9)

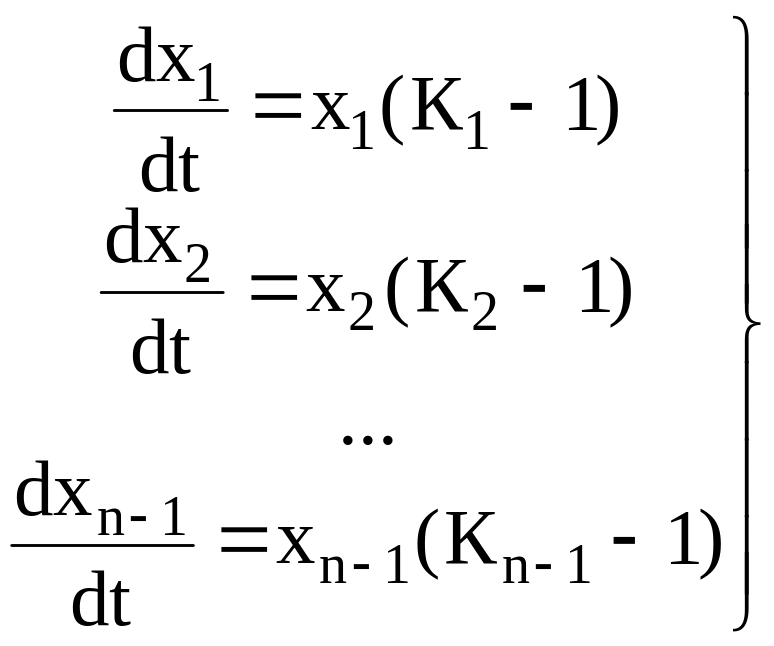(3.10)

В особых точках правые части равны нулю, что отвечает следующим случаям:

1. все К_i=1, y_i= х_i – реализуется n-компонентный азеотроп;

2. часть х_i =0, часть К_j=1 – реализуются азеотропы меньших размерностей, расположенные на границах концентрационного симплекса;

3. концентрации всех компонентов х_i , кроме одного (j), равны нулю, а К_j=1 – реализуется точка чистого компонента.

Линейное приближение получим, разложив в ряд Тейлора правые части уравнений (3.10) и беря первые производные.

В векторной форме уравнение первого приближения системы (3.10) имеет вид:

, (3.11)

где - координаты новой системы;

- матрица первых производных коэффициента распределения по составу:

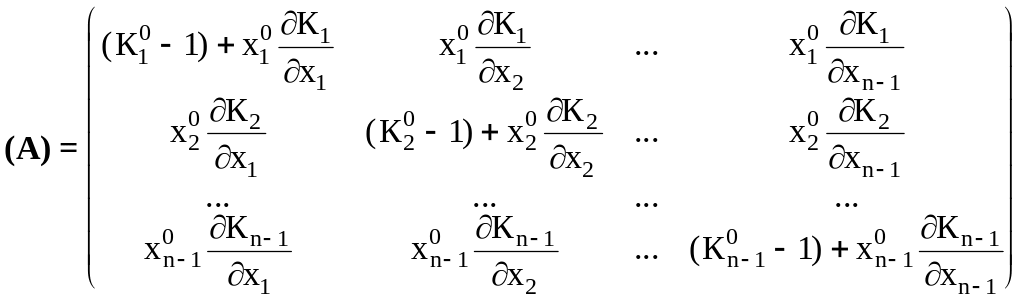(3.12)

Верхний индекс «0» означает, что производная берется в особой точке.

Матрица несимметрическая, поэтому для определения типов особых точек нам необходима дополнительная информация, которую можно почерпнуть из уравнений Ван-дер-Ваальса-Сторонкина, приведенных в разделе 2:

(2.11)

(2.12)

Здесь матрица вторых производных g-потенциала симметрическая и положительно определенная в силу устойчивости фаз.

Рассмотрим процесс, протекающий при изобарических условиях. Продифференцировав уравнение (2.11) в особой точке n-компонентного азеотропа по составу и наложив условия реализации азеотропной точки: grad T=0, y-x=0, получим:

(3.13)

Здесь матрицы (К) и (В) имеют следующий вид:

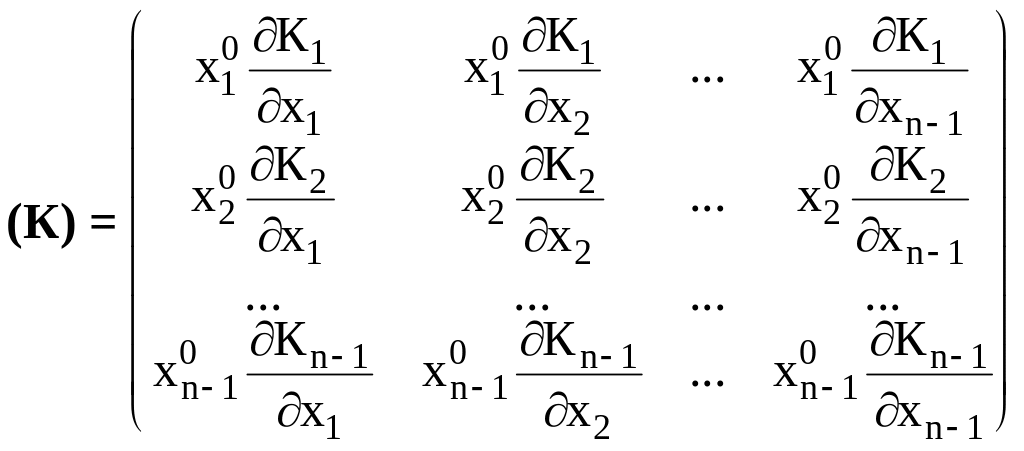(3.14)

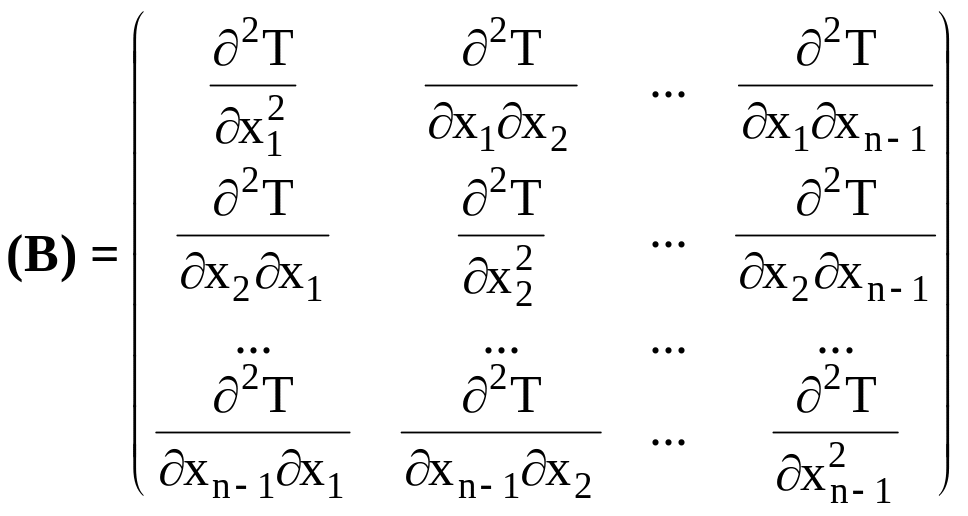(3.15)

Поскольку температура – скалярное свойство, то матрица симметрическая. Запишем уравнение (3.13) в ином виде и умножим обе ее части на матрицу, обратную :

(3.16)

Матрица также симметрическая и положительно определенная. Матрица получена умножением двух симметрических матриц и в силу этого она имеет только вещественные корни. Таким образом, система первого приближения (3.11) и система нелинейных дифференциальных уравнений (3.8), описывающих процесс дистилляции в окрестности особой точки, реализуют особые точки типа узел и седло.

Так как в уравнении (2.11) стоит знак минус перед скалярным множителем , то неустойчивый узел поля градиента температур переходит в устойчивый узел векторного поля нод жидкость-пар. Взаимное расположение указанных векторов приведено на рис. 2.1.

Связь между знаками корней  и типом особой точки в процессе дистилляции:

- если все  одного знака, то реализуется узловая точка (в рассматриваемом процессе все положительные  отвечают устойчивому узлу, все отрицательные  - неустойчивому узлу);

- если  разного знака, то реализуется седловинная точка, порядок седла равен числу отрицательных характеристических корней.

На рис. 3.1 показан ход дистилляционных линий в окрестности особых точек разных типов. В случае узловых точек все траектории сходятся в особой точке (устойчивый узел) или выходят из нее (неустойчивый узел). В случае седел - часть траекторий сходятся к особой точке, часть - выходят из нее и часть траекторий имеют в окрестности особой точки гиперболический ход, сначала приближаясь к ней, а потом удаляясь от нее. Таковы закономерности векторного поля равновесных нод жидкость-пар.

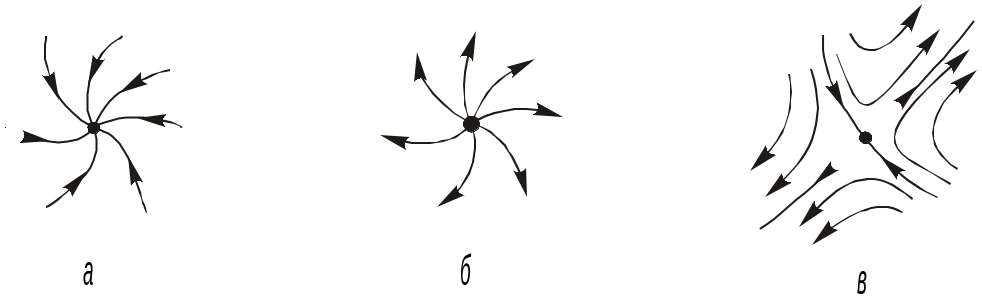
Рис. 3.1. Особые точки траекторий дистилляции в трехкомпонентных смесях: а - устойчивый узел; б - неустойчивый узел; в - седло

В целом закономерности поведения системы в окрестности особой точки названы, как уже отмечалось, локальными закономерностями диаграмм фазового равновесия "жидкость-пар" многокомпонентных систем. Они могут быть выражены в двух эквивалентных формах: в виде линий движения (процесс, протекающий в поле градиента скалярного свойства; процесс равновесного открытого испарения) и в топографическом виде (многообразия уровня, в частности, изотермо-изобары). Эта взаимосвязь вытекает из модифицированного уравнения Ван-дер-Ваальса-Сторонкина.

Взаимный качественный ход дистилляционных линий и изотермо-изобар приведен на рис. 3.2.