2. Термодинамические закономерности и моделирование фазовых равновесий

Фазовые равновесия различного типа играют важную роль при выборе методов разделения конкретных смесей. Так, например, ректификация базируется на законах о фазовом равновесии системы жидкость–пар, экстракция – жидкость–жидкость, адсорбция – газ–твердое тело или жидкость–твердое тело, абсорбция – газ–жидкость и т.д.

Для расчета массообменных процессов между отдельными фазами необходимо знать составы равновесных фаз при определенных температурах и давлениях. Наиболее надежно эти данные могут быть получены экспериментальным путем в соответствующих приборах. Так, например, данные по фазовому равновесию жидкость–жидкость, полученные при 20 °С, необходимы, главным образом, для предварительных оценок эффективности метода экстракции по сравнению с другими методами разделения, а также для расчета экстракционных установок, флорентийских сосудов, используемых при гетероазеотропной ректификации. Данные же по фазовому равновесию жидкость - жидкость, полученные при температурах кипения и атмосферном (реже при других) давлении, необходимы для расчета установок ректификации гетероазеотропных и расслаивающихся смесей.

Фазовое равновесие системы жидкость-пар для гомогенных (по жидкости) смесей чаще всего исследуется в изобарных условиях (процесс ректификации протекает при P=const).

Однако необходимо иметь в виду, что в реально отводимое время можно изучить фазовое равновесие только в системах, содержащих не более четырех компонентов. Более того, экспериментально можно получить только дискретные данные, тогда как для расчетов соответствующих процессов необходимо располагать аналитическим выражением, связывающим составы равновесных фаз. В связи с этим возникает задача получения аналитической зависимости состава одной фазы от другой в многокомпонентных системах. Такого рода зависимости моделируются с использованием соответствующих моделей с целью выяснения всех физико-химических ограничений на процесс разделения и для проведения автоматизированного проектирования соответствующих установок. В настоящее время моделирование осуществляется с использованием компьютерной техники и современных программных средств (Chemсad, PRO-II и др.).

Математические модели, отражающие взаимосвязь составов равновесных фаз, могут быть получены на основе физических представлений, удовлетворяющих термодинамике гетерогенных равновесий.

2.1. Термодинамические основы фазовых равновесий в многокомпонентных неидеальных системах

Если система, состоящая из r фаз и n компонентов, равновесна, то термодинамика позволяет установить взаимосвязь между различными ее переменными (температура, давление, состав и др.).

Для исследования общих качественных закономерностей фазового равновесия как бинарных, так и многокомпонентных многофазных систем может быть использовано термодинамическое уравнение фазового обмена, предложенное для бинарных смесей Ван-дер-Ваальсом и обобщенное на многокомпонентные смеси А.В. Сторонкиным.

Уравнение Ван-дер-Ваальса-Сторонкина представляет разность нулевых потенциалов равновесных фаз, выраженную в координатах потенциала Гиббса, и для двухфазной (жидкость-пар) n-компонентной системы в общем виде записывается следующим образом:

(2.1)

Здесь и — изменения объема и энтропии при фазовом дифференциальном переходе бесконечно малого количества смеси из жидкости в пар, равные соответственно,

(2.2)

(2.3)

g_ki - вторая производная g- потенциала, величина которой в силу устойчивости фазы всегда положительна. Для удобства восприятия жидкая фаза обозначена индексом «ж», паровая – индексом «п», а их составы, соответственно, х и y.

Уравнение (2.1) отнесено к составу жидкой фазы. Аналогичное уравнение может быть записано относительно изменения состава паровой фазы . В координатной форме уравнение (2.1) связывает полный дифференциал изменения температуры и давления при изменении состава с нодой . Здесь рассматриваются скалярные величины , и скалярное произведение двух векторов и .

Отметим, что для однокомпонентных смесей уравнение (2.1) превращается в обобщенное уравнение Клаузиуса; для двухкомпонентных смесей имеем классическое уравнение Ван-дер-Ваальса, на основе которого дается математическая интерпретация законов Коновалова и Вревского. С использованием уравнения (2.1) для случая трехкомпонентных систем было сформулировано правило Шрейнемакерса: при изотермическом испарении давление пара монотонно уменьшается, при изобарическом испарении температура кипения раствора монотонно возрастает.

Рассмотрим поведение трехкомпонентных систем при постоянном давлении. В этом случае температура кипения является функцией состава. При выборе в качестве независимых переменных dx₁ и dx₂ уравнение (2.1) имеет вид:

(2.4)

Выразим дифференциал температуры как функцию состава жидкой фазы:

(2.5)

и подставим значение dT в уравнение (2.4). В результате упрощения получим:

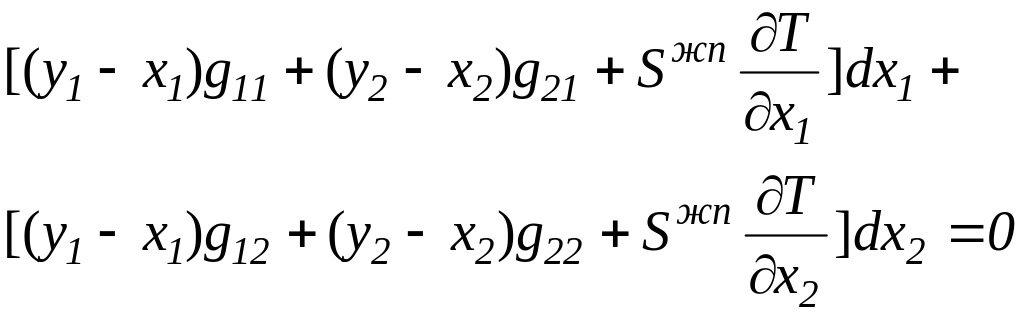(2.6)

Так как dx₁ и dx₂ независимые переменные, то уравнение (2.6) будет соблюдаться всегда только в случае, когда каждое из выражений при dx₁ и dx₂ равно нулю. Следовательно, уравнение (2.6) распадается на два, образующих систему уравнений типа

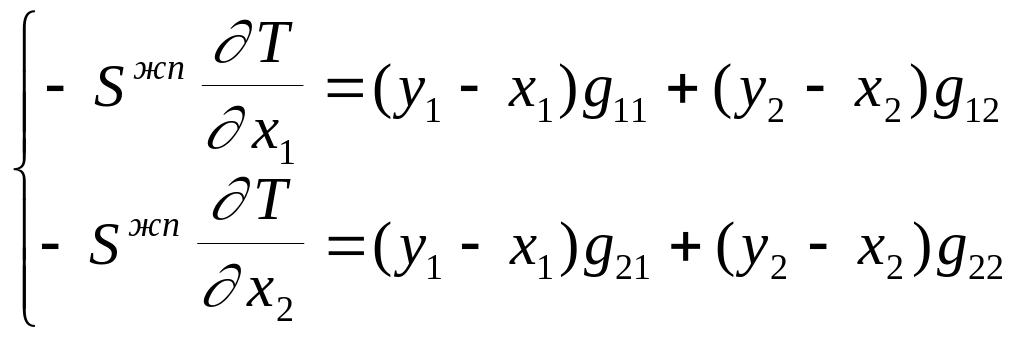, (2.7)

которую можно представить в векторной форме:

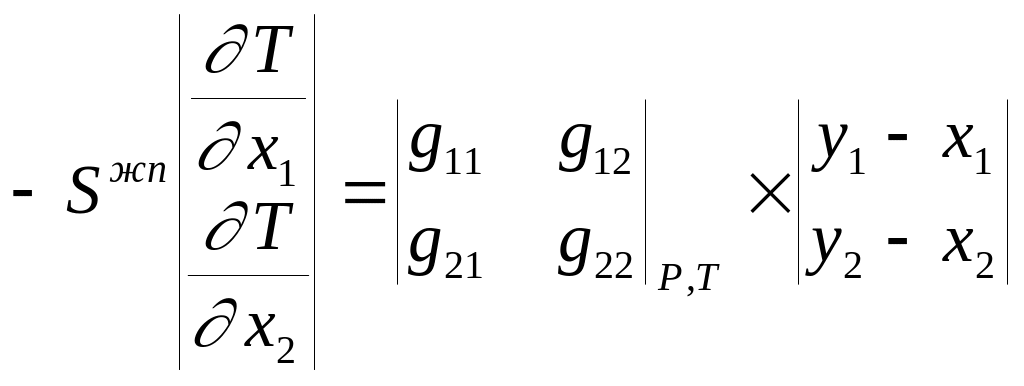(2.8)

Обобщая приведенный вывод на случай n-компонентной смеси, получим:

при Р=const

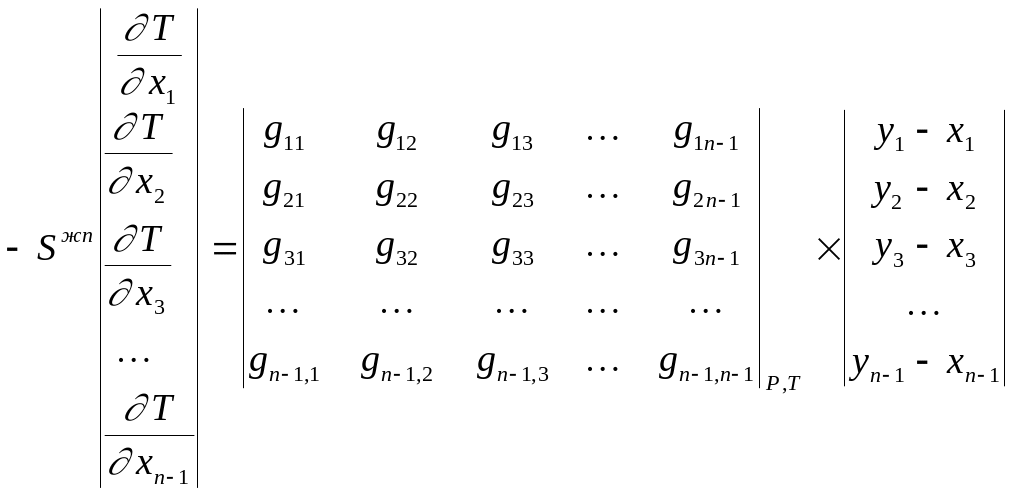(2.9)

при T=const (вывод аналогичен приведенному выше)

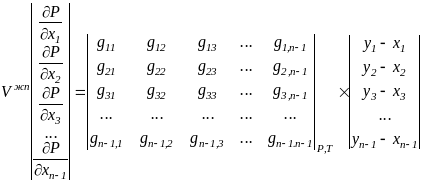(2.10)

И в сокращенном виде:

(2.11)

(2.12)

Уравнения (2.11) и (2.12) представляют модифицированную форму уравнения (2.1), которая является однозначным отображением векторного поля нод на поле градиента равновесных температур или давлений. Отображение рассматриваемого типа характеризуется переходом от одного поля к другому, топологически ему эквивалентному.

На рис. 2.1. приведено взаимное расположение векторов ноды и градиентов.

Уравнение Ван-дер-Ваальса – Сторонкина содержит всю информацию о гетерогенной системе в равновесных условиях.

При большем числе фаз уравнения типа (2.1) могут быть записаны для любой пары фаз, и фазовое равновесие будет представлено системой дифференциальных уравнений, в которой число независимых уравнений на единицу меньше числа фаз.

Рис. 2.1. Взаимное расположение векторов ноды жидкость-пар и градиента температур и давлений относительно изотермо-изобары

В уравнении Ван-дер-Ваальса – Сторонкина изобарно-изотермический потенциал Гиббса является характеристической функцией и позволяет определить все термодинамические свойства фазы. Частные производные от этого потенциала по числу молей одного из компонентов были названы химическими потенциалами. При переходе к концентрациям имеем, например, следующие выражения для бинарной смеси:

для удельного изобарно-изотермического потенциала фаз

(2.13)

(2.13а)

Из (2.13), (2.13а) с учетом , , следует:

(2.14)

(2.14а)

Для качественных исследований используется также уравнение для нулевого потенциала, которое имеет вид:

(2.15)

(2.15а)

Из этого уравнения, в частности, и выводится приведенное ранее уравнение Ван-дер-Ваальса – Сторонкина.

Условия равновесия между двумя фазами могут быть представлены следующим образом:

(2.16)

Следовательно, многофазная многокомпонентная система будет находиться в состоянии равновесия, если температуры, давления и химические потенциалы компонентов во всех фазах равны.

Для равновесного процесса условия (2.16) для смещения равновесия записываются в дифференциальной форме:

(2.16а)

Уравнение Ван-дер-Ваальса – Сторонкина полезно для качественных исследований поведения гетерогенных систем, а именно: для исследования общих закономерностей фазовых равновесий при различных способах изменения состава одной из фаз, исследования влияния температуры и давления на фазовое равновесие, общих свойств азеотропных смесей и т.д. На основе этого уравнения А.В. Сторонкиным и его учениками была построена общая качественная термодинамическая теория гетерогенных систем.

Что касается количественных закономерностей, то при решении дифференциальных уравнений возникают трудности, связанные с тем, что химические потенциалы не поддаются непосредственному экспериментальному определению. Поэтому на практике пользуются величинами, которые могут быть определены экспериментально и дают возможность оценивать значения химических потенциалов расчетным путем. В частности, такой величиной является фугитивность (летучесть), введенная Г. Льюисом. Обычно оценивают отношение летучести компонентов в реальных и стандартных условиях. В качестве стандартного состояния для реальных газов принимается состояние идеального газа при давлении, равном единице, и температуре, равной температуре реального газа. Для конденсированных фаз за стандартное принимается состояние чистой жидкости при температуре кипения раствора.

Учитывая, что уравнение фазового равновесия предусматривает равенство как химических потенциалов, так и стандартных химических потенциалов, обычно в исследованиях фазового равновесия жидкость–пар за стандартное состояние для обеих фаз принимается состояние чистого компонента при температуре кипения раствора как для жидкой, так и для паровой фаз.

Для описания свойств жидкой фазы, представляющей неидеальный раствор, введены понятия активности (а) и коэффициента активности (), которые определяются следующим образом:

(2.17)

Фазовое поведение идеальной системы жидкость-пар описывается законом Рауля:

(2.18)

где - давление насыщенных паров чистого i-го компонента.

Отклонения от идеальности учитываются введением соответствующих коэффициентов: активности для жидкой фазы и летучести для паровой фазы.

Фазовое поведение реальной системы жидкость-пар описывается в общем виде уравнением:

(2.19)

В случае отсутствия ассоциации в паровой фазе и при относительно небольших давлениях (1,5х10⁵ Па) можно считать паровую фазу идеальным газом. Для идеального газа . Неидеальность паровой фазы должна учитываться при повышенных давлениях или при наличии ассоциации молекул в паровой фазе.

Уравнение (2.19) широко используется для расчетов фазовых равновесий, так как при принятых допущениях оно имеет достаточную для инженерных расчетов точность.

Коэффициенты могут быть рассчитаны через вторые вириальные коэффициенты. Тогда, при наличии данных о давлениях паров чистых компонентов, задача моделирования фазового равновесия жидкость-пар сводится к нахождению зависимости коэффициентов активности отдельных веществ от состава жидкой фазы.