8.1. Тройные системы

Графический метод построения балансовых сетей (в приложении к трехкомпонентным системам) позволяет наглядно представить преимущества перехода к балансовым (продуктовым) симплексам при исследовании схем с рециклами, выявить границы области функционирования схемы, обусловленные фазовым поведением системы, и разработать алгоритм аналогичного исследования комплексов разделения смесей с большим числом компонентов.

Рассмотрим простейший комплекс разделения тройной смеси АВС с выделением двух контуров размерности два (на рис.8.1 они очерчены пунктиром).

Для контура, охватывающего вторую и третью колонны, общий баланс потоков и баланс по компонентам (А, В) выражаются системой уравнений:

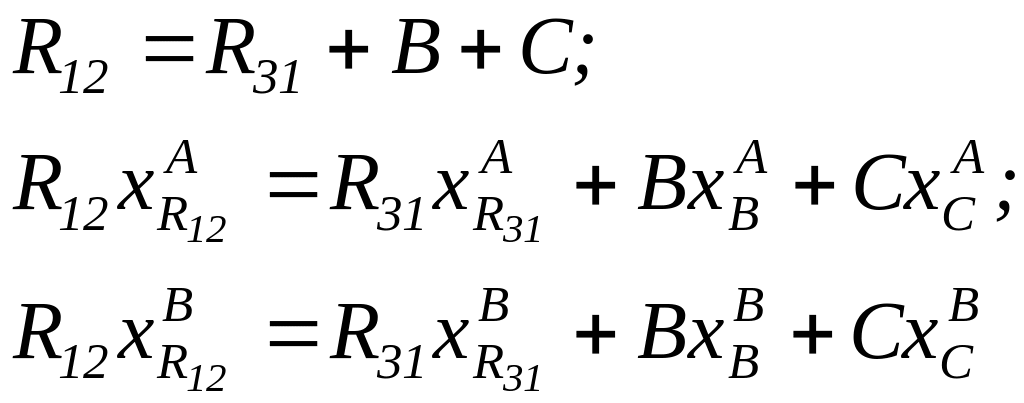(8.1)

Здесь В, С - количества продуктовых потоков; R_ij - количество потока, поступающего их колонны i в колонну j; х_l^m - концентрация m-го компонента в l-ом потоке. Количества всех потоков представлены в кмоль/час, концентрации компонентов - в молярных долях.

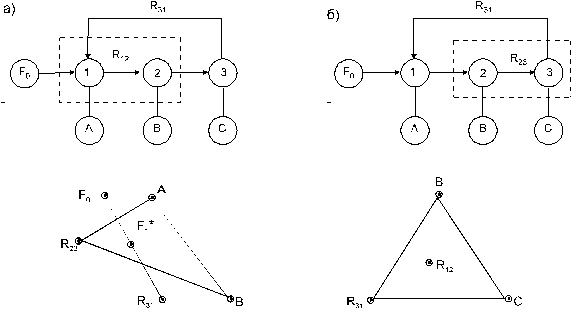
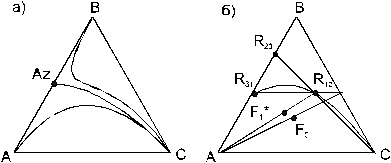
Рис. 8.1. Определяющие контуры и соответствующие им балансовые симплексы: F₁*, R₁₂ - центры тяжести симплексов.

Отнеся количества всех потоков к потоку R₁₂, получим в векторной форме:

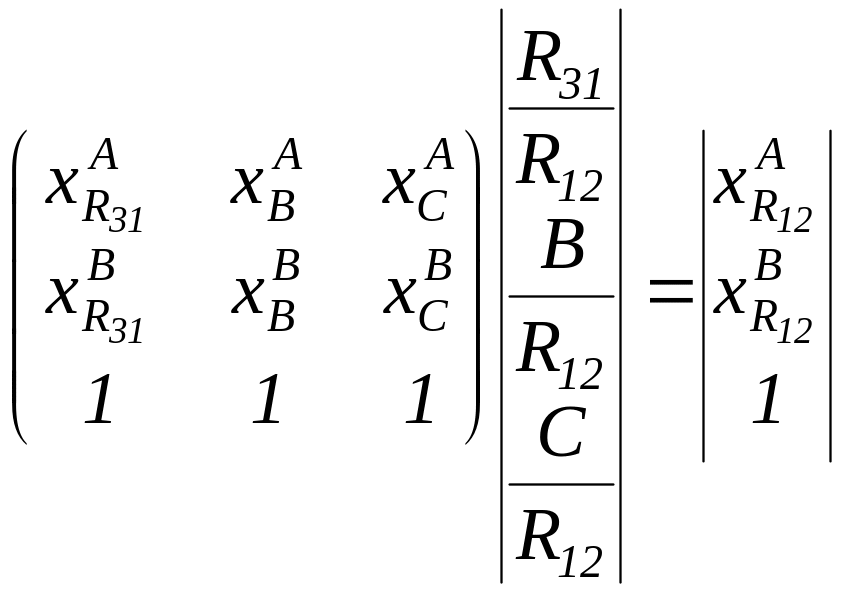(8.2)

Данная система неоднородных линейных уравнений имеет единственное решение при условии, что определитель матрицы составов не равен нулю. Из общей теории линейных неоднородных уравнений следует, что в зависимости от расположения вектора распределение знаков величин а₁=R₃₁/R₁₂, а₂=B/R₁₂, a₃=C/R₁₂ имеет вид, приведенный на рис. 8.2. Положительное значение величины а₁, а₂, а₃ будут иметь только в том случае, если ненулевая точка постоянного вектора находится внутри продуктового симплекса ВСR₃₁ (рис. 8.1, б). Поскольку комплекс ориентирован на выделение чистых компонентов, то стороны ВС концентрационного и продуктового симплексов совпадают. На рис. 8.2 представлена общая картина знаков величин потоков для двух различных составов рецикла R₃₁. Для контура, охватывающего колонны 1 и 2, ход рассуждений аналогичный (рис. 8.1, а).

Для рассмотренного примера отметим два следствия, вытекающих из этого положения: 1) если точка брутто-состава потока R₁₂ лежит на стороне R₃₁С, то поток В равен нулю, т.е. все поступающее с потоком R₁₂ вещество В распределяется между потоками R₃₁ и С; 2) если точка состава R₁₂ лежит ниже стороны R₃₁С, то поток В меняет свой знак и баланс контура вырождается в пересечение двух одномерных симплексов В+R₁₂=R_31­+С.

В соответствии с приведенными закономерностями сформулируем необходимое условие соблюдения балансовых соотношений. Необходимым условием соблюдения балансового соотношения в контуре является расположение точки брутто-состава входящего в контур потока внутри балансового симплекса (в нашем случае треугольника), отвечающего выходящим потокам.

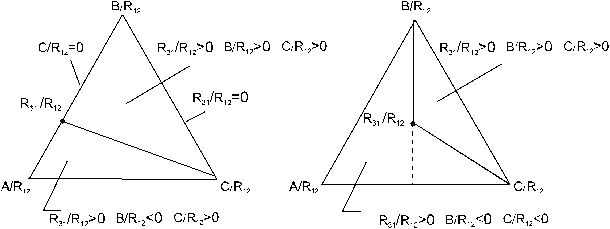
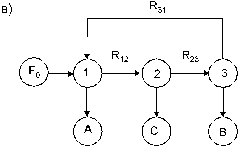
Рис. 8.2. Общая картина знаков потоков в балансовых симплексах.

Сформулированное условие принадлежности точки состава брутто-питания продуктовому симплексу является необходимым, но не достаточным. Из балансовых соотношений для комплекса в целом вытекает, что и, таким образом, точка состава суммы потоков В и С определяется пересечением секущей со стороной ВС концентрационного треугольника. Координата этой точки О: . Тогда уравнение общего материального баланса контура, охватывающего вторую и третью колонны, можно привести к виду: R₁₂=R₃₁+O. Очевидно, если рецикл R₃₁ определен, то результирующий поток R₁₂ будет иметь состав, лежащий на отрезке, соединяющем точки и R₃₁ (рис.8.3). Этот отрезок является геометрическим местом точек - центров тяжести продуктового треугольника ВСR₃₁.

Конкретный состав потока R₁₂ определяется с учетом термодинамических ограничений фазовой диаграммы. Данный вывод приводит в соответствие заданное разделение и материальный баланс контура (рис. 8.1,б) и является необходимым и достаточным условием их согласованности.

Для контура, охватывающего первую и вторую колонны, уравнение материального баланса имеет вид: F₀+R₃₁=А+В+R₂₃, и балансовая сеть представлена пересечением одномерного (F^*=F₀+R₃₁) и двумерного (F^*=А+В+R₂₃) симплексов (рис. 8.1,а). Точка брутто-питания F^* должна лежать в пределах треугольника АВR₂₃ (рис.8.4) - необходимое условие; и принадлежать отрезку, соединяющему составы и R₂₃ (необходимое и достаточное условие).

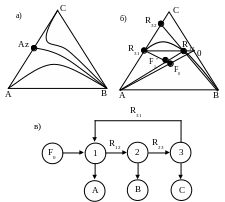
Рис 8.3. Структура диаграммы фазового равновесия (а), линии материального баланса (б) и простейший комплекс разделения (в) трехкомпонентной смеси.

З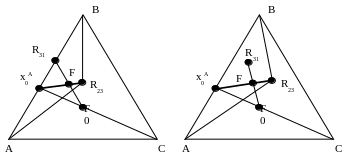 десь линия также является геометрическим местом точек - центров тяжести продуктового симплекса. Одновременно состав брутто-питания F^* принадлежит балансовому симплексу AR₁₂ , что следует из рассмотрения контура, охватывающего первую колонну комплекса.

Рис. 8.4. Согласованность материального баланса и заданного разделения в контуре, охватывающем первую и вторую колонны

Обобщим приведенные выше рассуждения. Если пространственный контур характеризуется наличием нескольких входных и выходных потоков, то каждой группе потоков соответствует свой балансовый симплекс (комплекс). Центры тяжести балансовых симплексов (комплексов) смешения и разделения должны совпадать, т.е. точка потока брутто-питания должна располагаться не на границе и не вне симплекса, а внутри него. Таким образом, по любому контуру потоки (с учетом их количеств, составов и ограничений на составы) должны удовлетворять условию реализации обобщенного центра тяжести, выполнение которого свидетельствует о соответствии балансовых соотношений заданному качеству продуктов и наличии стационарного режима работы комплекса разделения многокомпонентной смеси закрепленного состава. Иными словами: если среди пар балансовых симплексов (комплексов) найдется пара, пересечение которой пусто, то технологический комплекс не имеет стационарного состояния, удовлетворяющего принятому заданному разделению.

Частное условие, соответствующее стационарному режиму комплекса, можно представить в виде: . Следует уточнить, что при закрепленном порядке выделения компонентов выводы справедливы для ограниченной области составов исходных смесей.

Таким образом, в рассмотренных примерах определяющим является симплекс, соответствующий балансовому уравнению (8.3,а) третьей колонны, а фактором, лимитирующим работоспособность схемы, выступает форма сепаратрисы и ее расположение в концентрационном симплексе. Пересечение двух балансовых симплексов размерности один (линий смешения и разделения) однозначно определяет координату обобщенного центра тяжести и наличие стационарного режима работы разделительного комплекса. Отсутствие такого пересечения свидетельствует об обратном. По-видимому, выбор определяющего пространственного контура достаточно сложен, особенно для схем с большим числом аппаратов и рецикловых потоков, и должен осуществляться на основе полного анализа всех независимых балансовых уравнений.

Рассмотрим аналогичную систему АВС, характеризуемую наличием бинарного азеотропа АС и разделяющей определенной кривизны (рис. 8.5, а).

Рис. 8.5. Структура диаграммы фазового равновесия (а), линии материального баланса (б) и простейший комплекс разделения (в)

трехкомпонентной смеси

Разделение такой смеси возможно с использованием простейшего комплекса, колонны которого работают при одном и том же давлении. На рис. 8.5, б приведена балансовая сеть комплекса разделения исходной смеси F₀, состав которой расположен со стороны вогнутости сепаратрисы. При построении балансовой сети сохраняется допущение о четкости разделения, то есть достижении разделяющих или границ симплекса. Согласно структуре диаграммы, если на первой колонне выделяется практически чистый компонент А, то состав R₁₂ должен в пределе лежать на разделяющей линии. Поток R₂₃ не имеет ограничений по составу и может достигнуть стороны треугольника АC. Для выделения компонента C из потока R₂₃ необходимо, чтобы разделяющая линия была обращена выпуклостью к углу треугольника, соответствующему компоненту C. Т. е. здесь также должно выполняться условие . В качестве рецикла R₃₁ целесообразно использовать азеотропный состав (для диаграммы-антипода ход рассуждений аналогичный).

Такой краткий анализ возможных разделений смеси заданного состава показывает, что основное ограничение, обусловленное структурой фазовой диаграммы, связано с положением разделяющего многообразия относительно продуктовых потоков, то есть с геометрическими свойствами диаграммы. На рис. 8.6 приведены различные положения разделяющей в исследуемой системе.

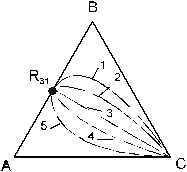
Рис. 8.6. Различные положения разделяющей линии в тройной системе при сохранении топологического типа (класс 3.1.0 - 2)

В случаях (1) и (2) состав потока R₁₂ лежит внутри продуктового симплекса; потоки В, С, R₃₁ имеют один и тот же знак и необходимое условие работоспособности комплекса выполнено. При прямолинейной разделяющей (3) состав R₁₂ лежит на стороне ВR₃₁ продуктового треугольника, поток С равен нулю и, следовательно, компонент С будет накапливаться в системе. Рецикл R₃₁ азеотропного состава возрастает до бесконечного количества и, соответственно, поток R₁₂ , постепенно меняя свой состав, приближается к азеотропному составу (комплекс неработоспособен). При положениях (4) и (5) состав R₁₂ лежит вне продуктового симплекса, поток С меняет свой знак, и комплекс не разделит исходную смесь на чистые компоненты.