26 Вариант
1. Решить матричное уравнение: ,
где
,
,
,
.
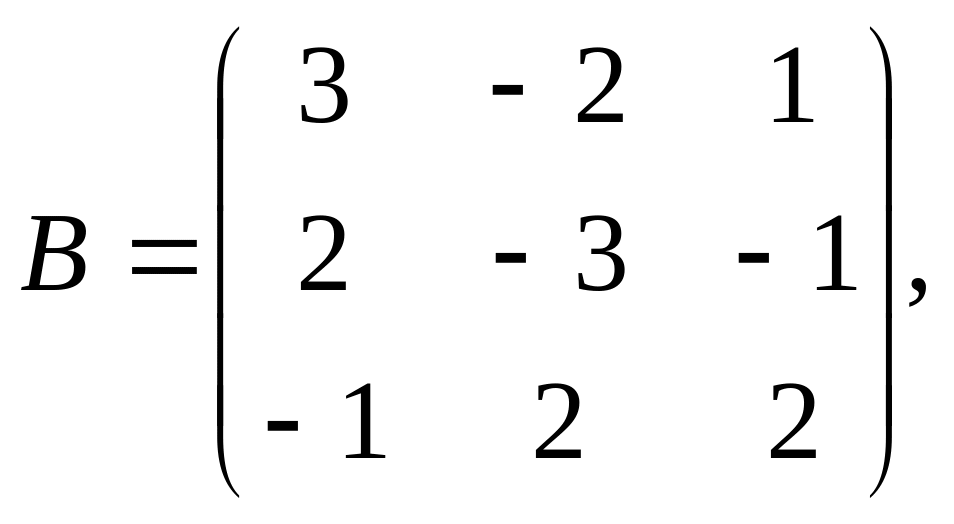
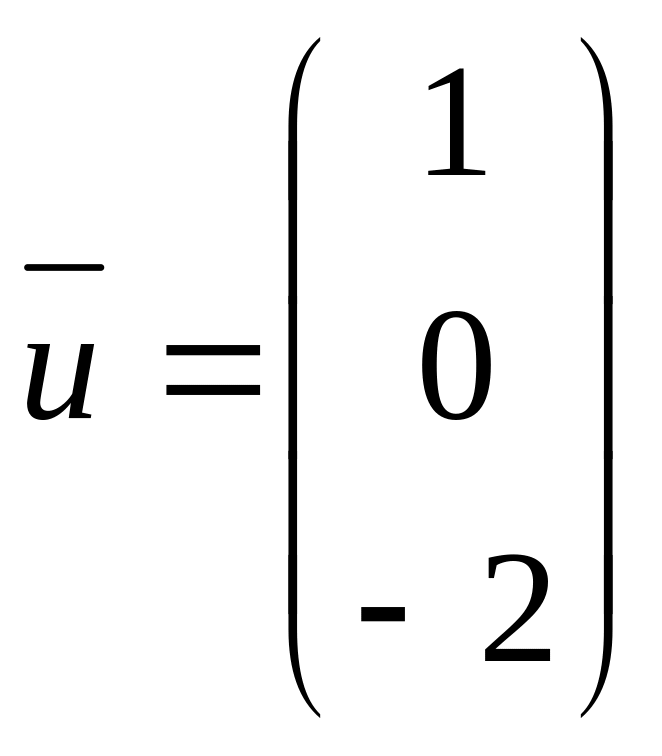Полученный результат проверить подстановкой.
2. Даны векторы
Установить, при каких значениях параметра векторы образуют базис. Найти координаты вектора в базисе . Полученную систему решить с помощью обратной матрицы.
.
3. Решить систему по формулам Крамера.
,
,
.
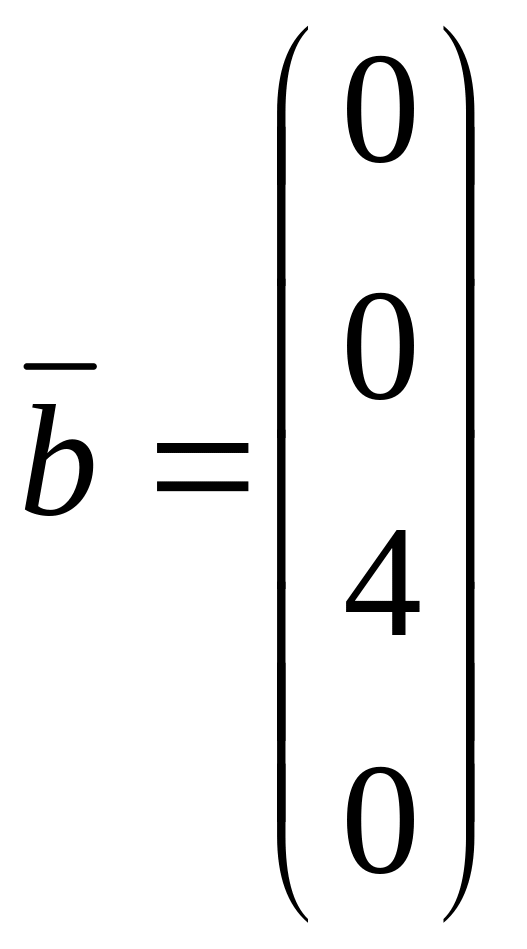4. Исследовать системы на совместность. Совместные системы решить методом Гаусса.
,
.
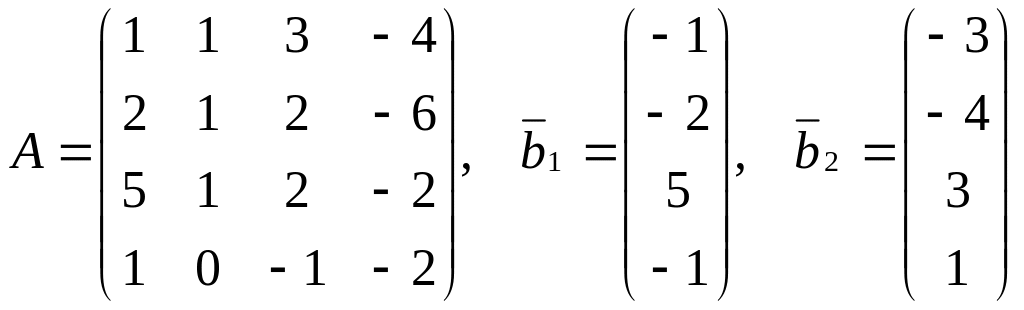5. Найти собственные числа и собственные
векторы матрицы
6. Привести уравнение кривой второго порядка к каноническому виду, сделать чертёж:
27 Вариант
1. Решить матричное уравнение: ,
где
,
,
.
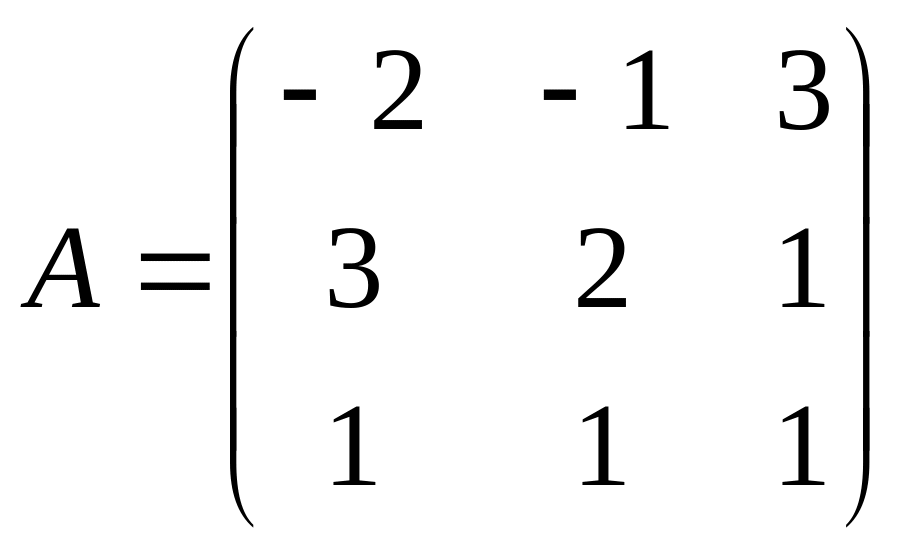Полученный результат проверить подстановкой.
2. Даны векторы
Установить, при каких значениях параметра векторы образуют базис. Найти координаты вектора в базисе . Полученную систему решить с помощью обратной матрицы.
.
3. Решить систему по формулам Крамера.
,
,
.
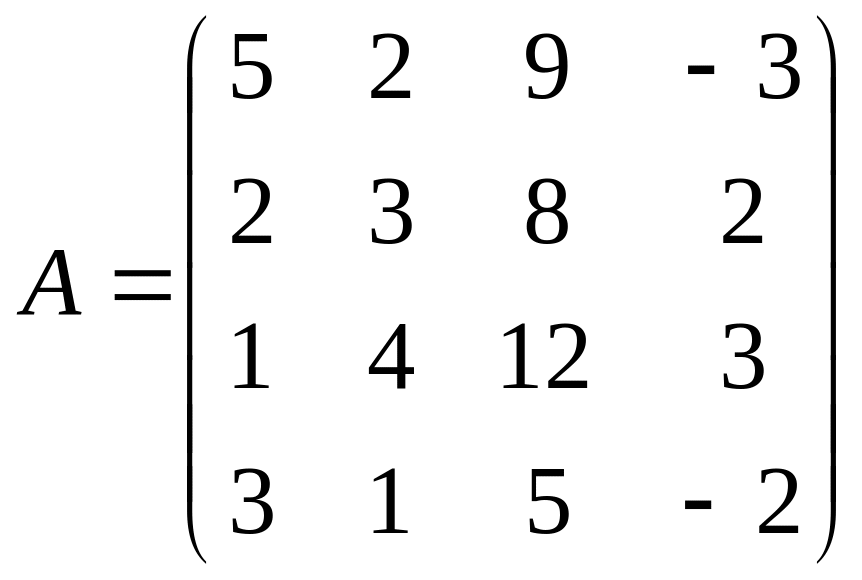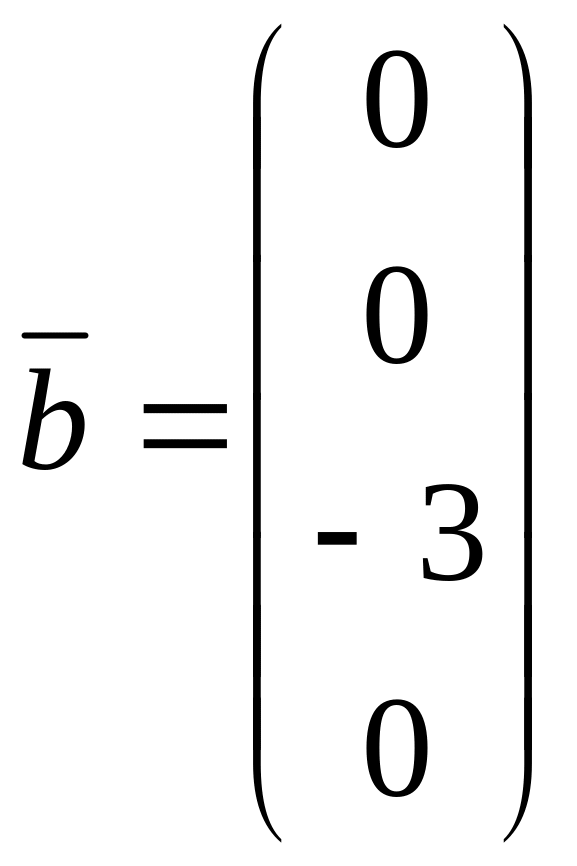4. Исследовать системы на совместность. Совместные системы решить методом Гаусса.
,
.
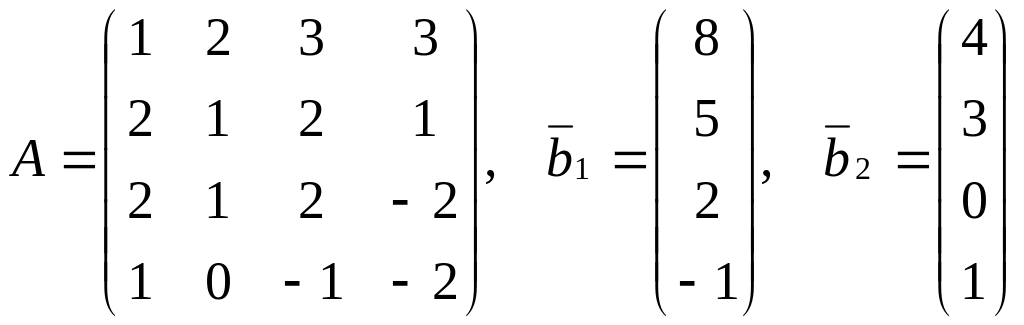5. Найти собственные числа и собственные
векторы матрицы A=
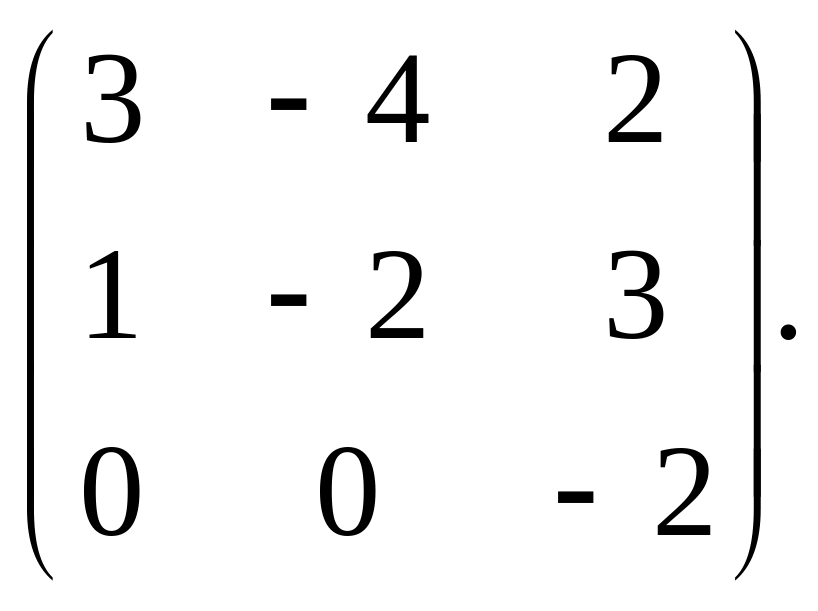
6. Привести уравнение кривой второго порядка к каноническому виду, сделать чертёж:
28 Вариант
1. Решить матричное уравнение: ,
где
,
,
,
=
.
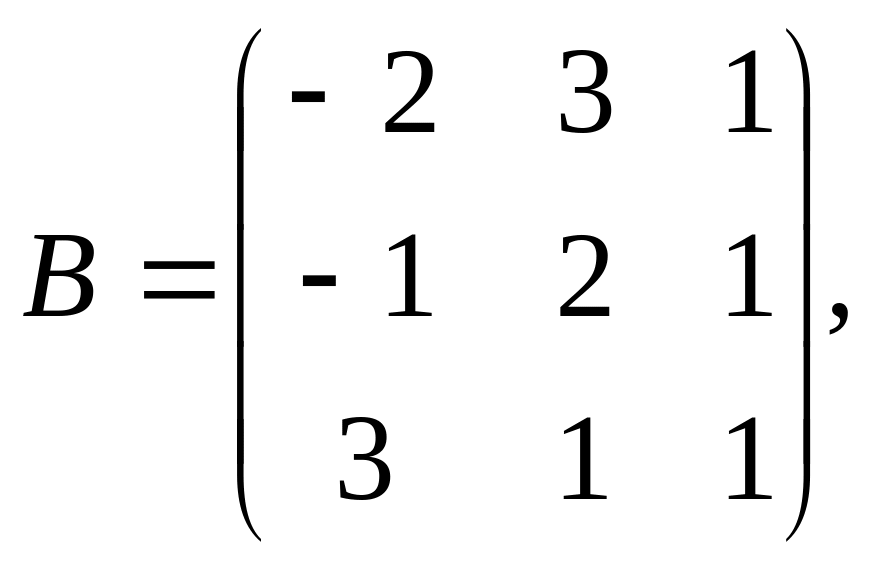Полученный результат проверить подстановкой.
2. Даны векторы
Установить, при каких значениях параметра векторы образуют базис. Найти координаты вектора в базисе . Полученную систему решить с помощью обратной матрицы.
.
3. Решить систему по формулам Крамера.
,
,
.
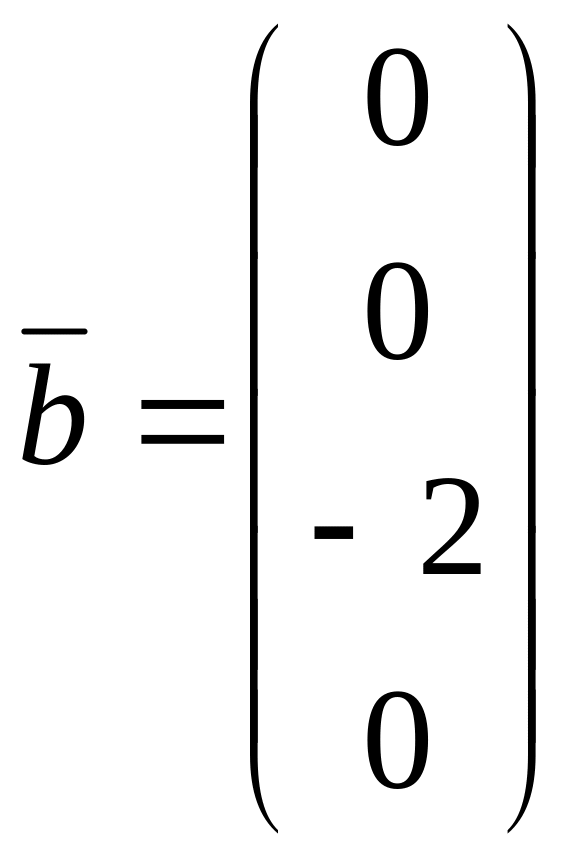4. Исследовать системы на совместность. Совместные системы решить методом Гаусса.
,
.
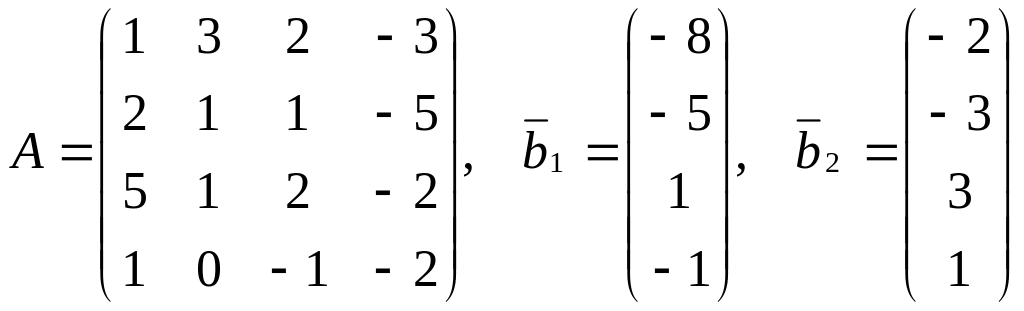5. Найти собственные числа и собственные
векторы матрицы
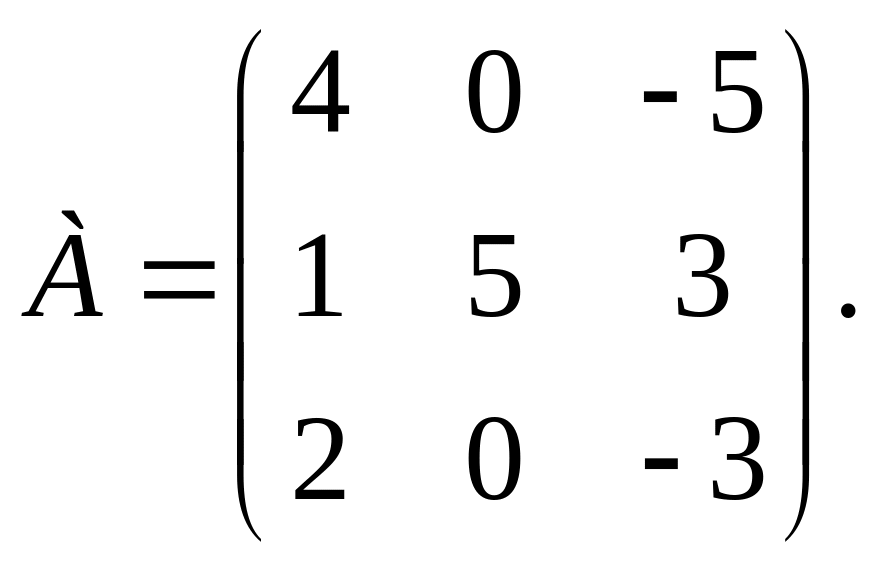
6. Привести уравнение кривой второго порядка к каноническому виду, сделать чертёж:
29 Вариант
1. Решить матричное уравнение: ,
где
,
,
.
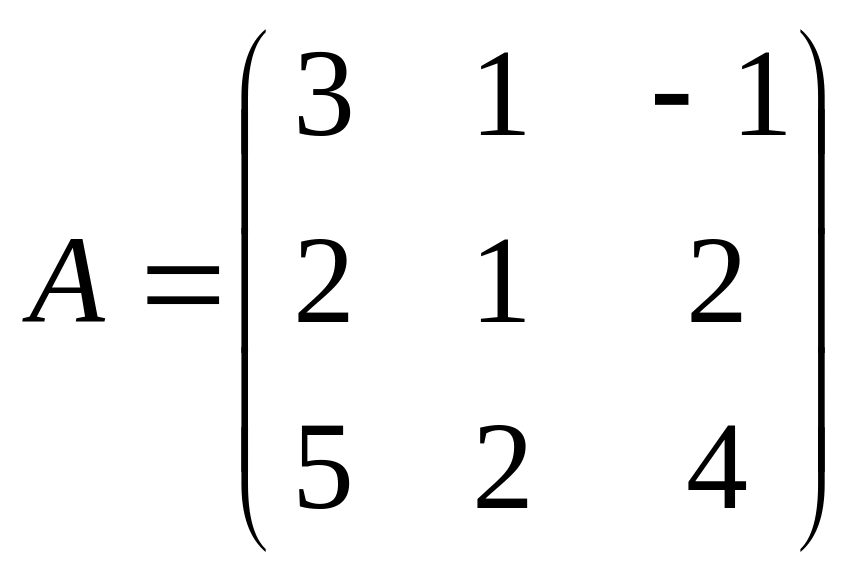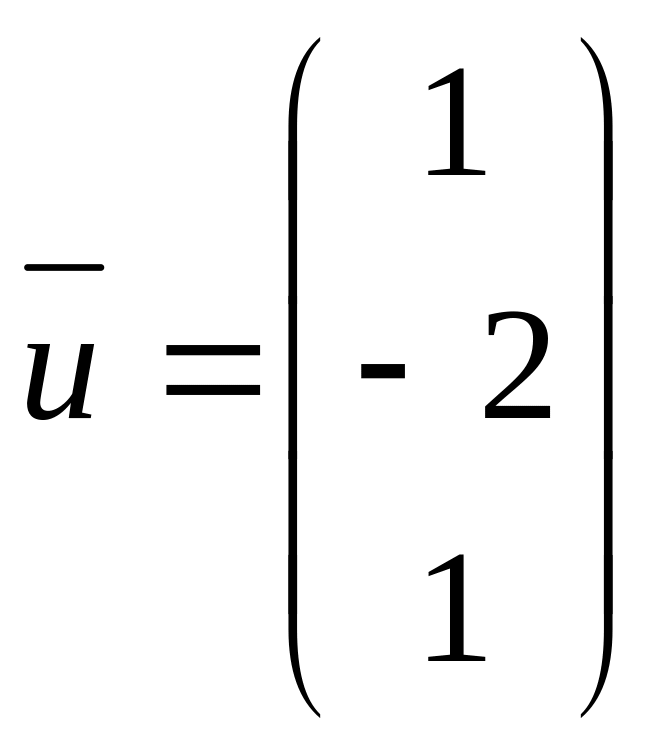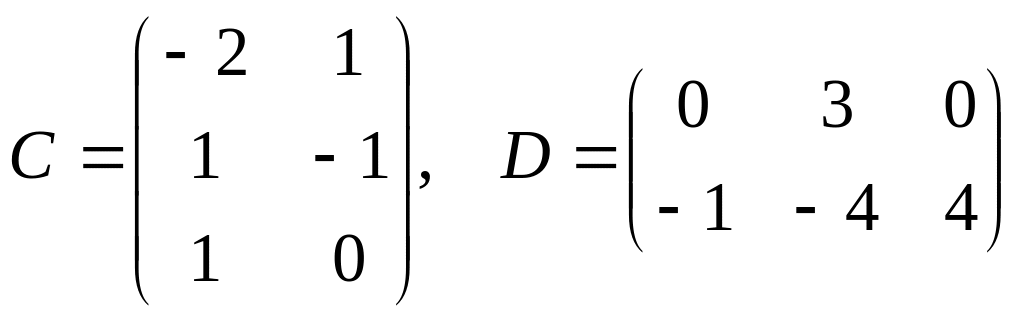Полученный результат проверить подстановкой.
2. Даны векторы
Установить, при каких значениях параметра векторы образуют базис. Найти координаты вектора в базисе . Полученную систему решить с помощью обратной матрицы.
.
3. Решить систему по формулам Крамера.
,
,
.
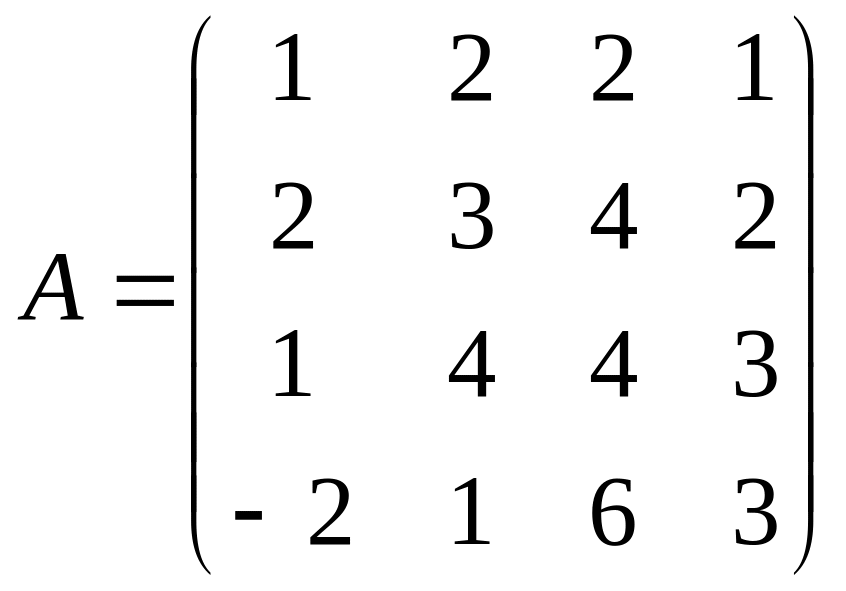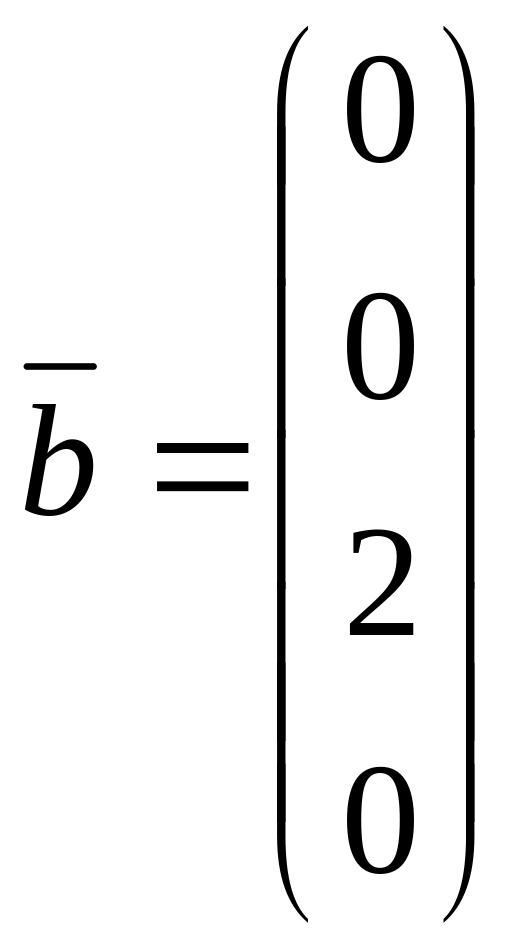4. Исследовать системы на совместность. Совместные системы решить методом Гаусса.
,
.
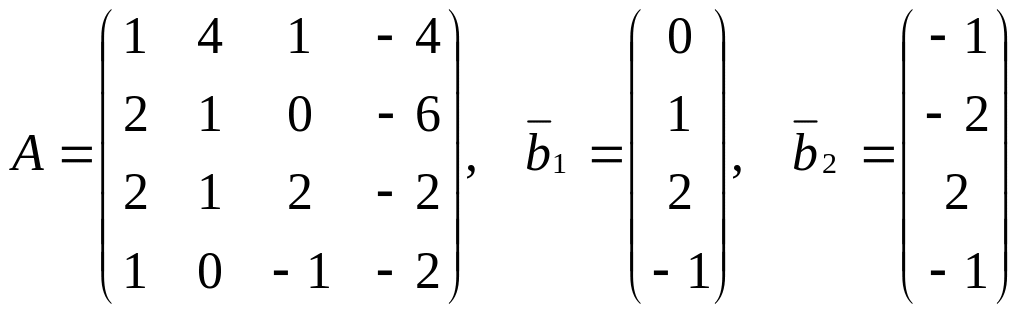5. Найти собственные числа и собственные
векторы матрицы A=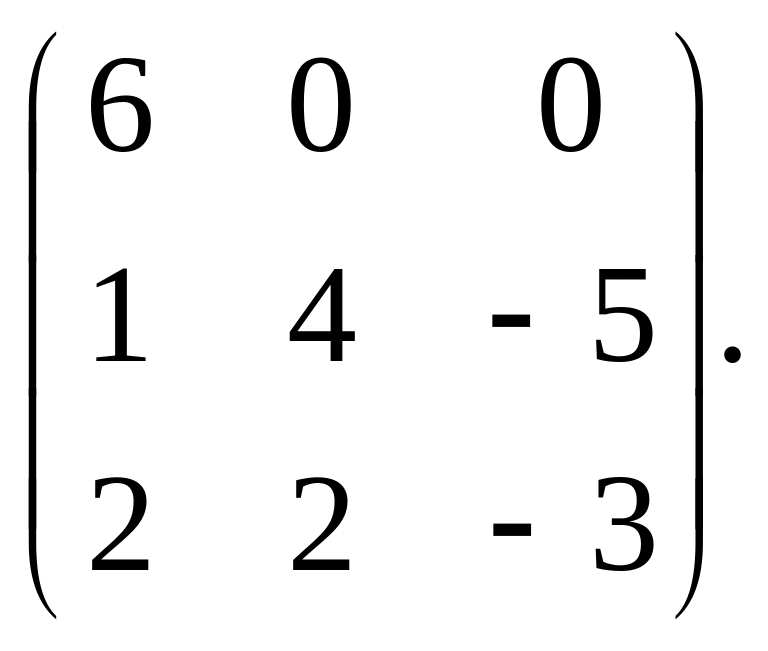
6. Привести уравнение кривой второго порядка к каноническому виду, сделать чертёж:
30 Вариант
1. Решить матричное уравнение: ,
где
,
,
,
=
.
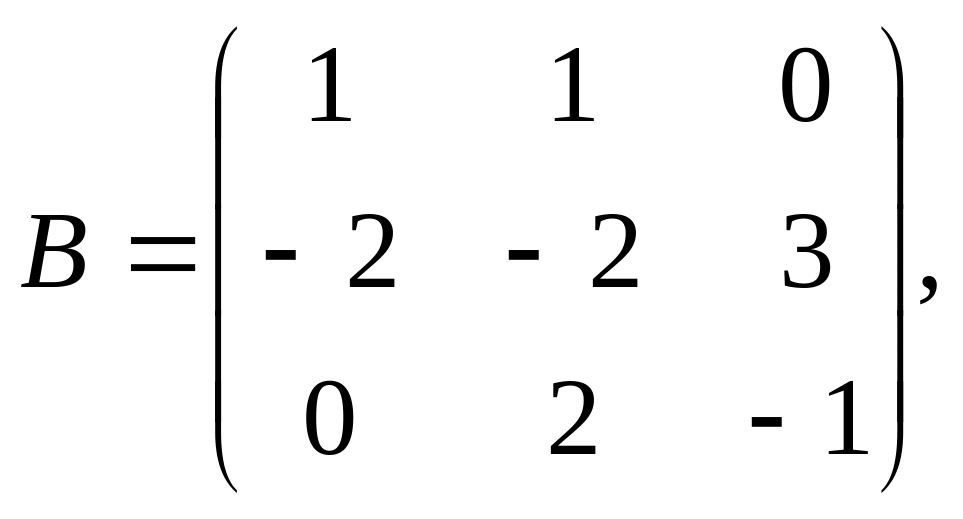
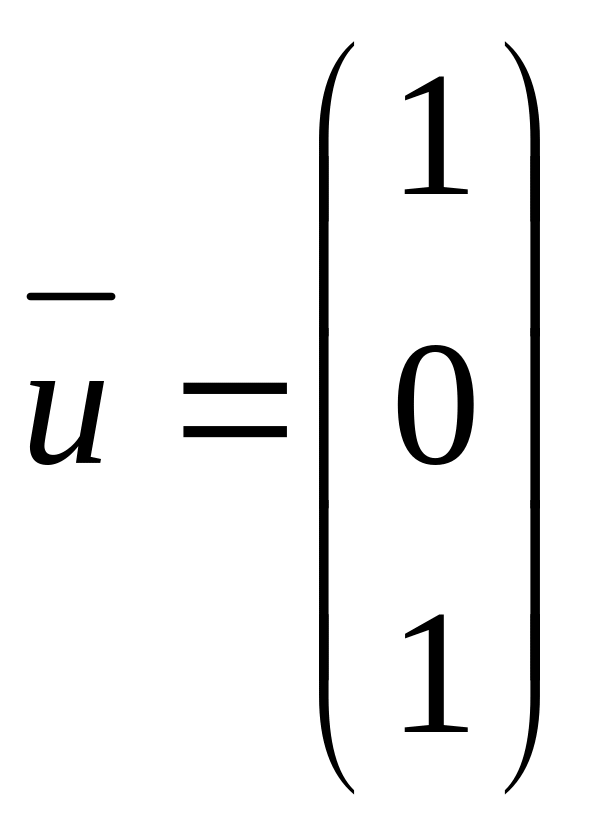Полученный результат проверить подстановкой.
2. Даны векторы
Установить, при каких значениях параметра векторы образуют базис. Найти координаты вектора в базисе . Полученную систему решить с помощью обратной матрицы.
.
3. Решить систему по формулам Крамера.
,
,
.
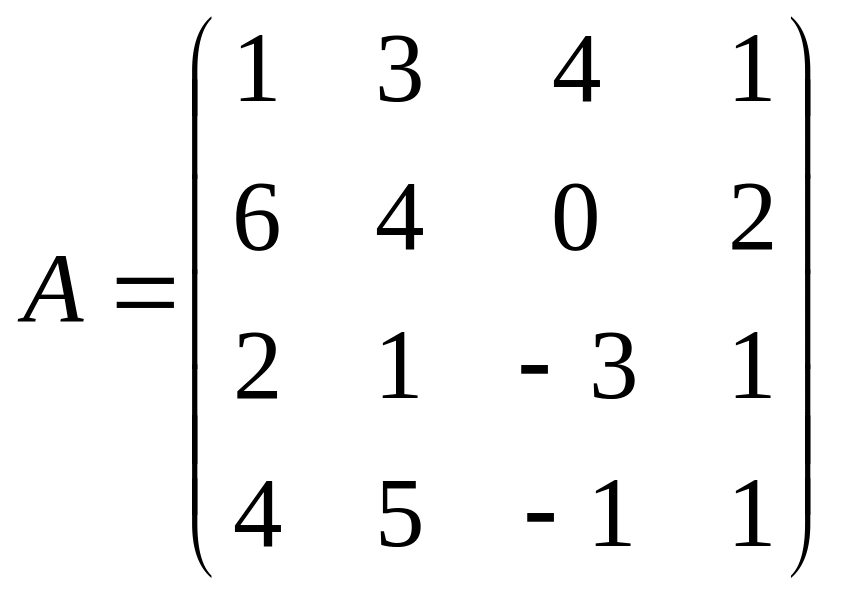4. Исследовать системы на совместность. Совместные системы решить методом Гаусса.
,
.
5. Найти собственные числа и собственные
векторы матрицы
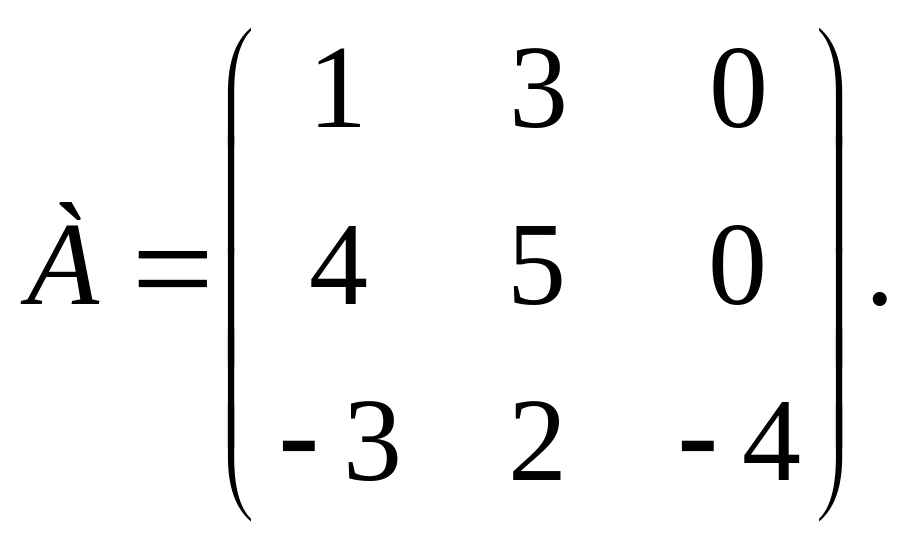
6. Привести уравнение кривой второго порядка к каноническому виду, сделать чертёж:
Приложение
Образец титульного листа
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет»
кафедра «Высшая математика»
ТИПОВОЙ РАСЧЁТ №
по высшей математике
(линейная алгебра)
вариант №
Выполнил: студент группы …
Проверил: преподаватель …
Ижевск
2012
Список литературы
Основная литература:
1. Бугров Я.С., Никольский С.М. Высшая математика. Элементы линейной алгебры и аналитической геометрии. -Т.1.—М.: Дрофа, 2004.-282с.
2. Клетеник Д.В. Сборник задач по аналитической геометрии /Под ред. Н.В. Ефимова.- СПб.: Профессия.-2003.-200с.
Дополнительная:
Айзикович А.А., Гусельникова Г.В., Шпилькин И.А. Типовые расчёты по высшей математике (линейная алгебра).- Ижевск, ИМИ, 1988.