
- •1 Способ
- •2 Способ
- •Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •27 Вариант
- •28 Вариант
- •29 Вариант
- •30 Вариант
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет»
кафедра «Высшая математика»
ТИПОВЫЕ РАСЧЁТЫ
по высшей математике
(линейная алгебра)
Ижевск
2012
УДК 512.64(07)
Рецензент: Ицков А.Г., кандидат физико-математических наук, доцент кафедры «Прикладная математика и информатика»
Типовые расчёты по высшей математике (линейная алгебра)/Сост. А.В.Данелян, Н.Р.Корякина.-Ижевск:Изд-во ИжГТУ,2012.-46с.
. В пособии представлены 30 вариантов типовых расчётов, рассмотрены некоторые теоретические вопросы по курсу линейной алгебры, приведены примеры решения задач типового расчёта. Методическое пособие предназначено для технических специальностей ИжГТУ. Может быть использовано студентами других специальностей.
Справочный материал
Обозначения:
1)
![]() -
некоторые константы (скаляры);
-
некоторые константы (скаляры);
2)
![]() - векторы;
- векторы;
3)
![]() =(
=(![]() -
-
![]() мерный
вектор-строка, где
мерный
вектор-строка, где
![]() -
элементы (координаты) вектора
;
-
элементы (координаты) вектора
;
4)
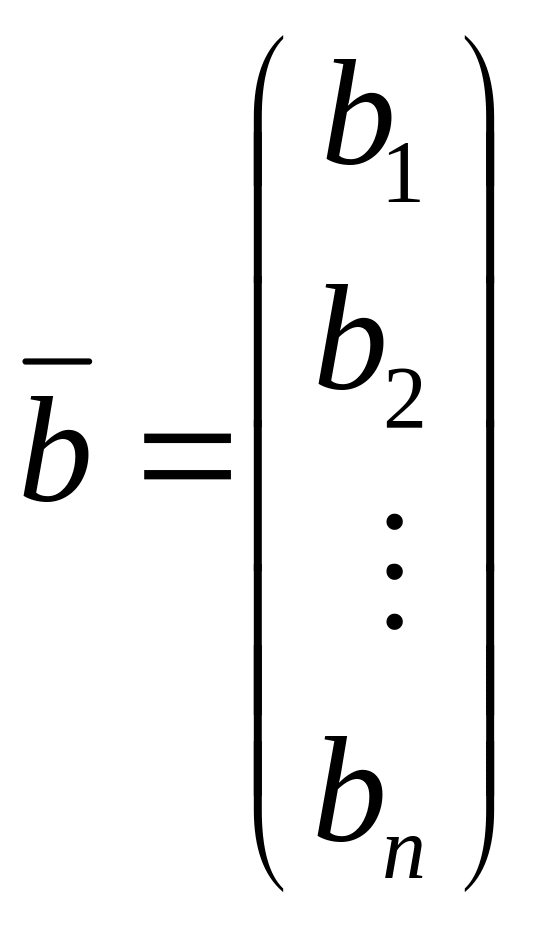 -
мерный
вектор-столбец;
-
мерный
вектор-столбец;
5)
![]() – матрицы;
– матрицы;
6)
![]() - элементы матриц
.
Первый индекс
- элементы матриц
.
Первый индекс
![]() указывает номер строки, второй индекс
указывает номер строки, второй индекс
![]() - номер столбца;
- номер столбца;
7)
![]() - матрица размерности
- матрица размерности
![]() ,
где
,
где
![]() -
количество строк,
-
количество строк,
![]() -
количество столбцов;
-
количество столбцов;
8)
![]() =
=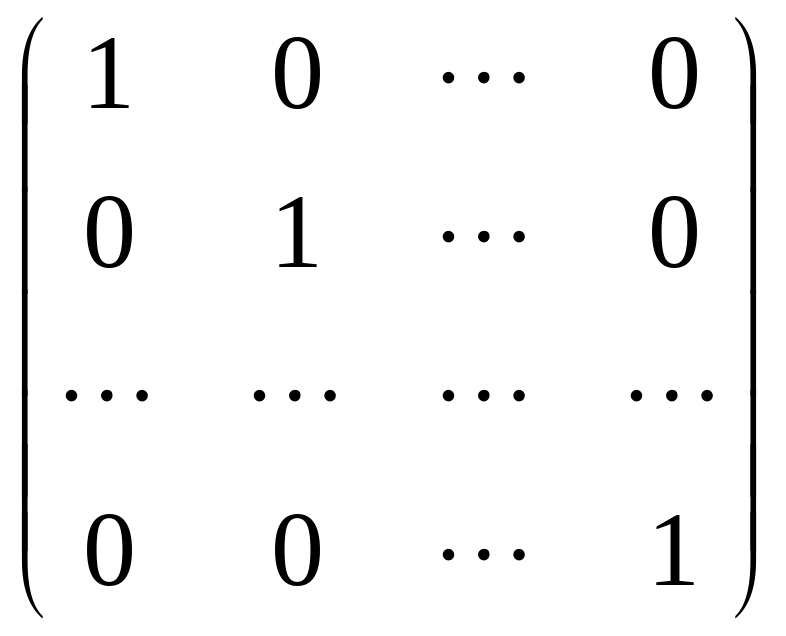 - единичная матрица размерности
- единичная матрица размерности
![]() в пространстве
в пространстве
![]()
9)
![]()
![]() - определитель матрицы
- определитель матрицы
![]() ;
;
10)
![]() - алгебраическое дополнение элемента
- алгебраическое дополнение элемента
![]() матрицы
;
матрицы
;
11)
![]() - символ транспонирования;
- символ транспонирования;
12) rang =rg - ранг матрицы ;
13) A-1 - обратная матрица.
Свойства определителей
1)
![]() ;
;
2) det![]() ;
;
3) det![]() ;
;
4)
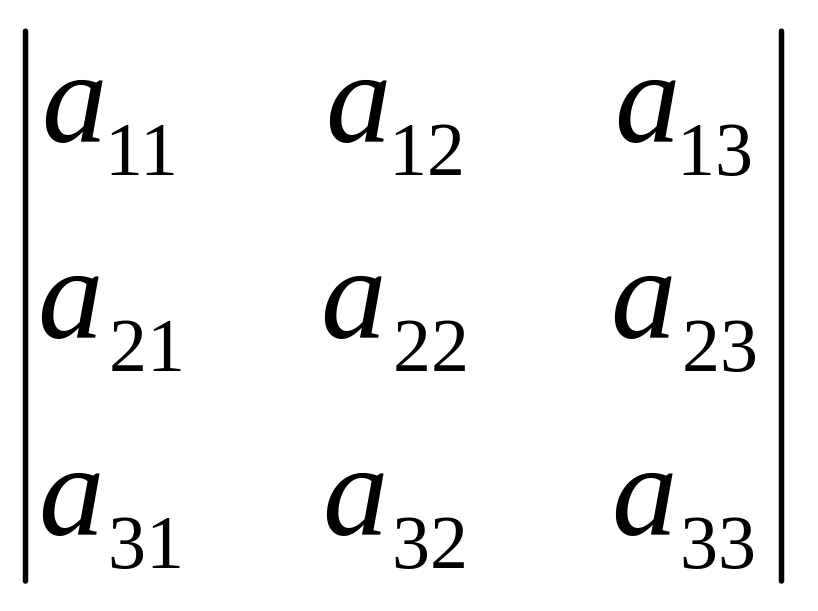 =
=![]() .
.
Свойства линейных операций над матрицами
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5) (![]() ;
;
Свойства операции транспонирования матрицы
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]()
5)
![]()
Свойства операции умножения матриц
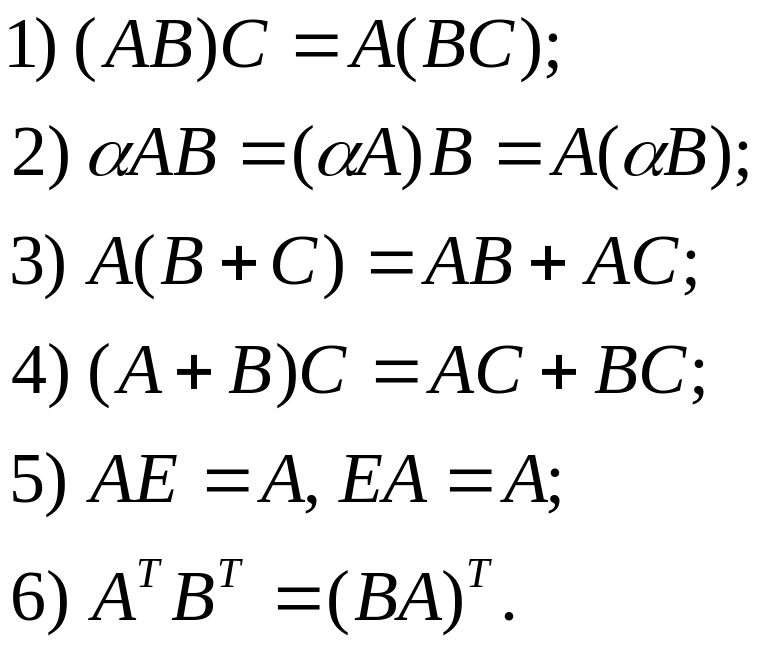
Свойства обратной матрицы

Общие требования к оформлению типового расчёта
В типовом расчёте должны быть решения всех задач одного из предложенных вариантов. Оформление следует выполнять вручную (кроме титульного листа) на бумаге формата А4. Текст размещается на одной стороне листа. Объём работы зависит от количества задач. Титульный лист оформляется по образцу (см. приложение).
Работа должна содержать:
![]() номер и условие задачи
номер и условие задачи
решение
ответ.
Эти три части должны быть отделены друг от друга.
Примеры решения задач типового расчёта
Задача 1
Решить матричное уравнение:
![]() ,
,
где
![]() ,
,
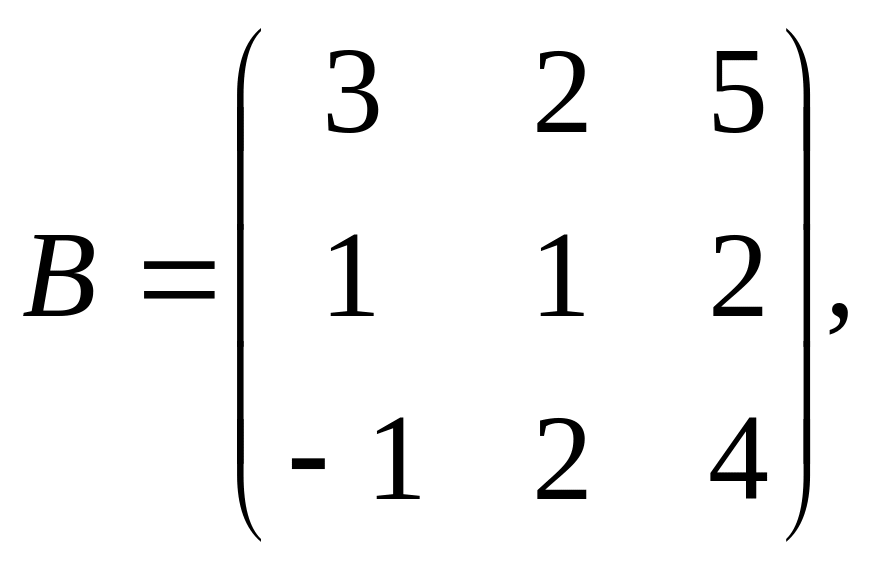
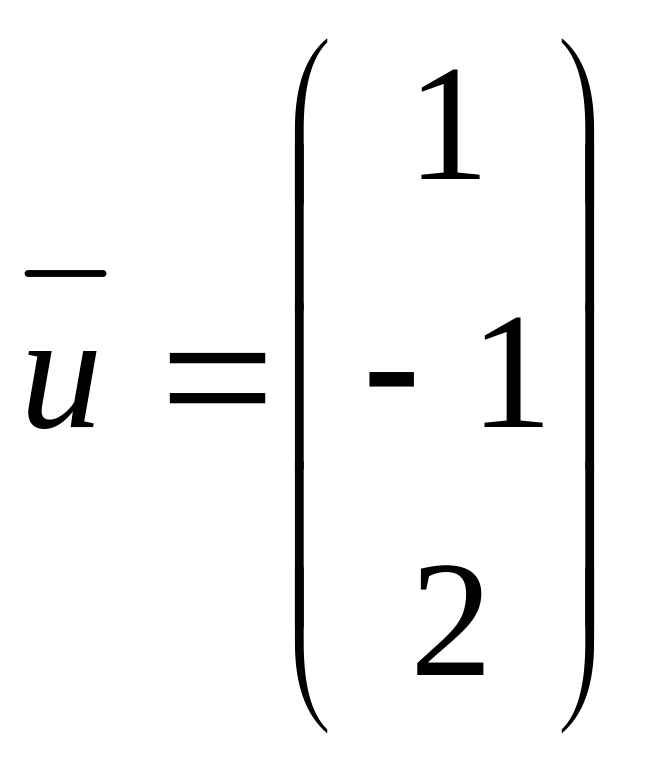 ,
,
![]() ,
,
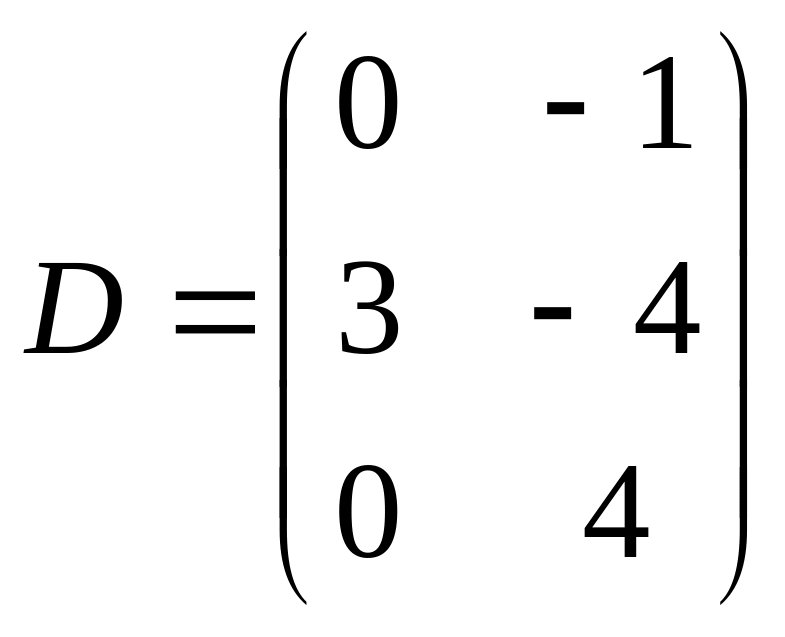 .
.
Полученный результат проверить подстановкой.
Решение
Проводя преобразования исходного уравнения, получим
![]() ,
откуда
,
откуда
![]()
![]() .
.
Найдём матрицу, обратную матрице
,
т.е.
![]() :
:
![]() ,
,
где![]()
![]() -
транспонированная матрица алгебраических
дополнений.
-
транспонированная матрица алгебраических
дополнений.
=![]() .
.
Окончательно
![]() =
=![]() .
.
Аналогично находим
![]() :
:
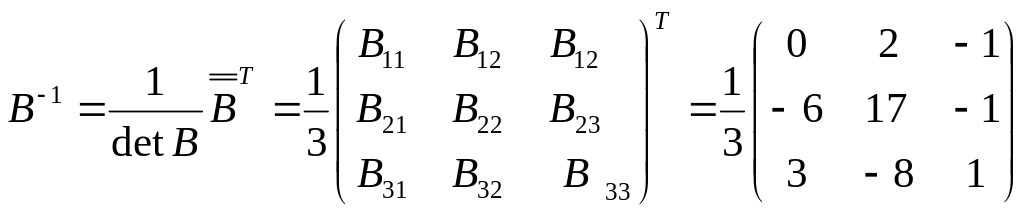 .
.
Найдём теперь матрицу (![]() :
:
(
=
![]() .
.
Тогда
![]() =
=
![]()
 .
.
Здесь матрица
=![]()
Окончательно
![]() .
.
Задача 2
Даны векторы
![]()
1.Установить, при каких значениях
параметра
![]() векторы
образуют базис в пространстве
векторы
образуют базис в пространстве
![]() .
.
2. Найти координаты вектора
![]() в базисе
в базисе
![]() .
Полученную систему решить с помощью
обратной матрицы.
.
Полученную систему решить с помощью
обратной матрицы.
![]()
Решение
1. Если
![]() )
)![]() ,
то векторы
образуют базис.
,
то векторы
образуют базис.
)=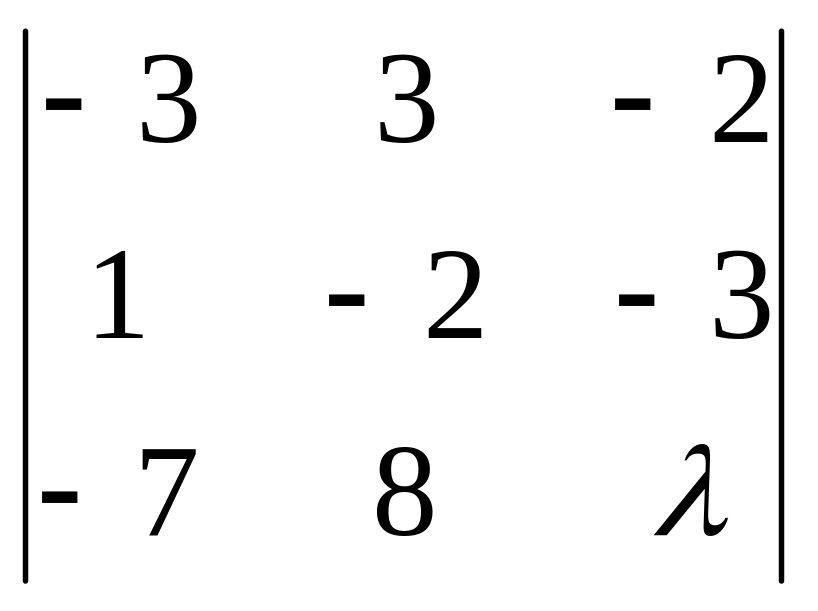 =6
=6![]() Следовательно, при
Следовательно, при
![]() ,
векторы
образуют базис.
,
векторы
образуют базис.
2. Пусть
![]() - координаты вектора
- координаты вектора
![]() в базисе
.
Тогда
в базисе
.
Тогда
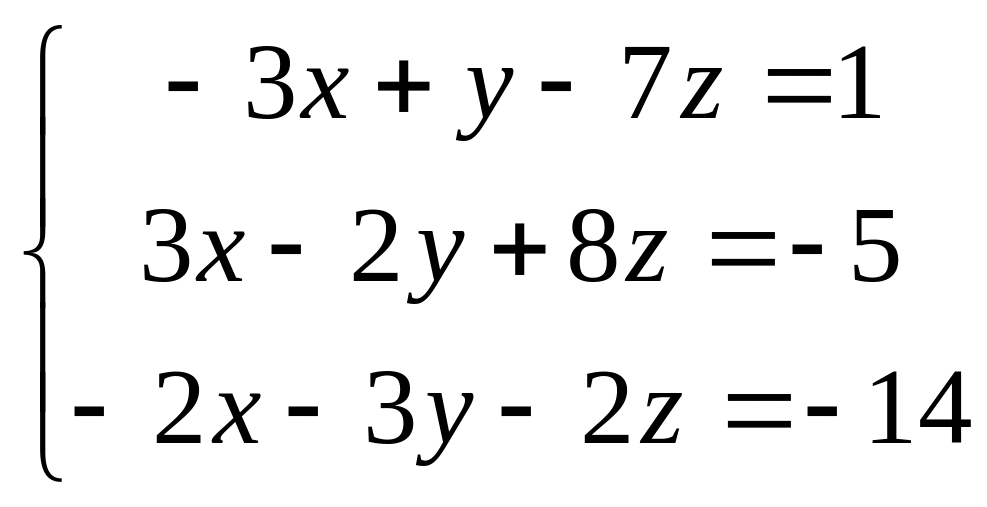 .
.
Решим эту систему матричным способом:
![]() ,
,
где
 матрица-столбец
неизвестных,
матрица-столбец
неизвестных,
![]() матрица,
обратная основной матрице системы
матрица,
обратная основной матрице системы
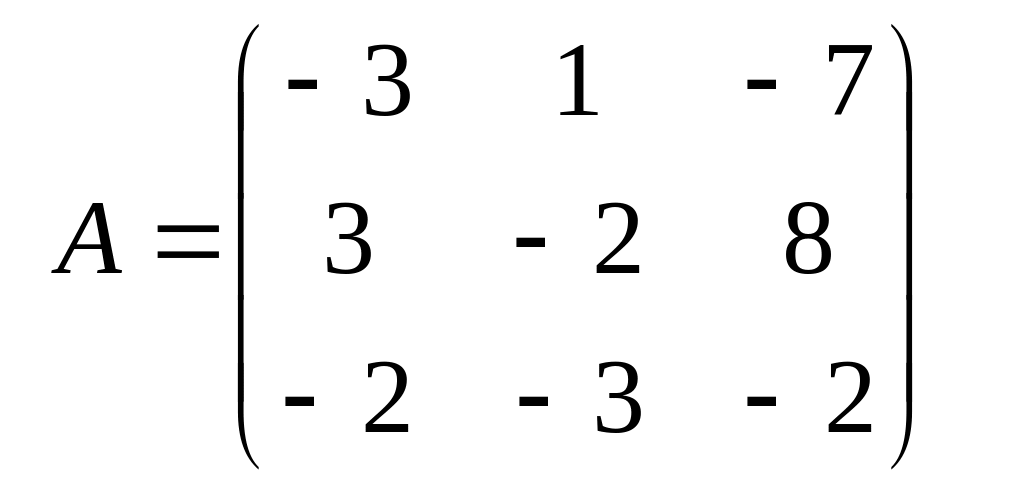 ,
,
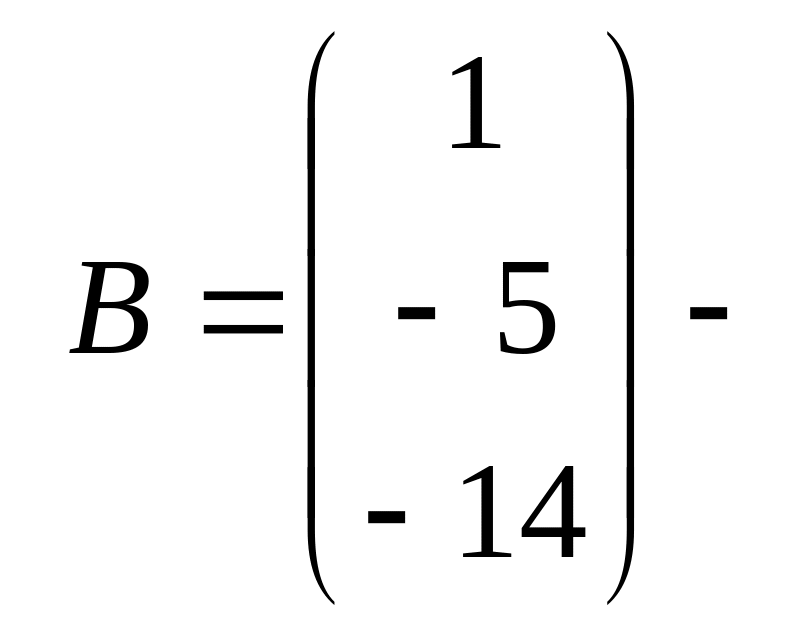 матрица-столбец
свободных членов.
матрица-столбец
свободных членов.
Найдём
![]()
.
Здесь
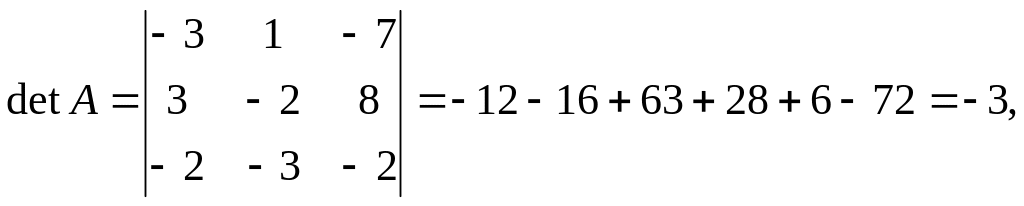
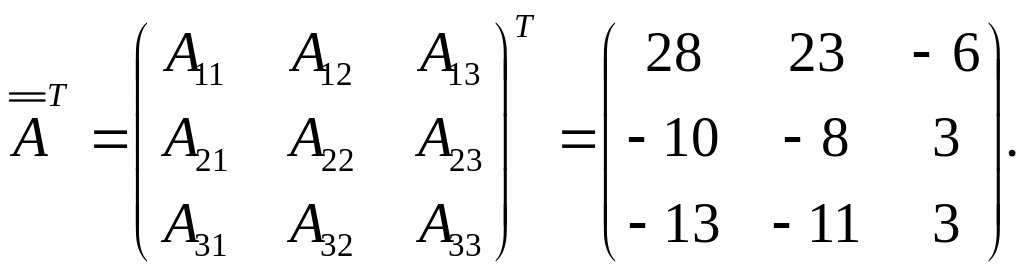
Распишем элементы последней матрицы:
![]()
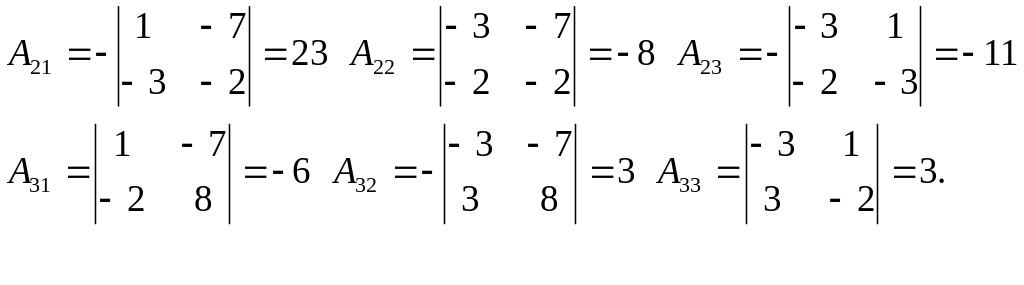
Таким образом,
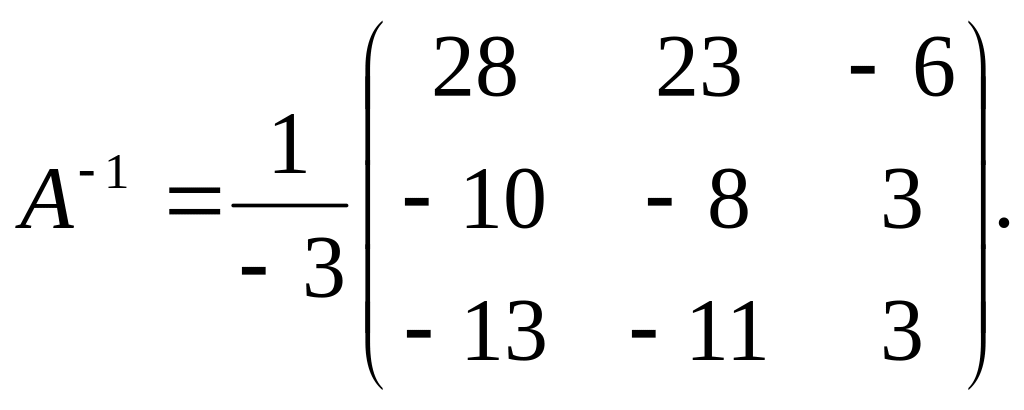
Сделаем проверку:
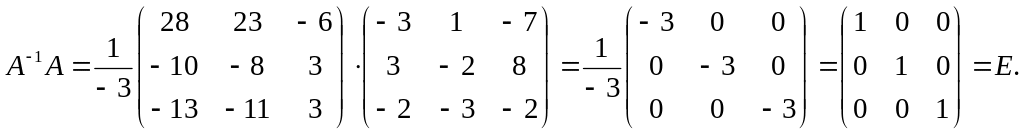
Найдём теперь матрицу-столбец неизвестных:
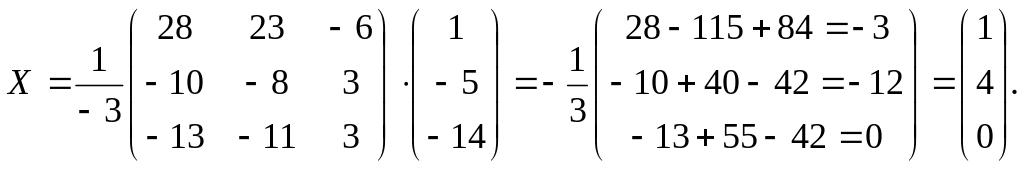
Разложение вектора по базисным векторам имеет вид:
=![]() .
.
Задача 3
Решить систему
![]() по формулам Крамера.
по формулам Крамера.
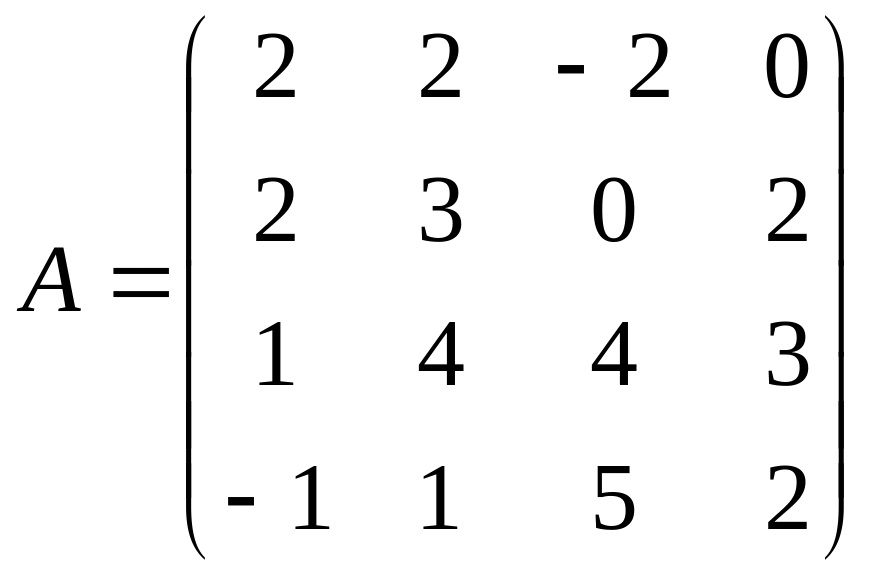 ,
,
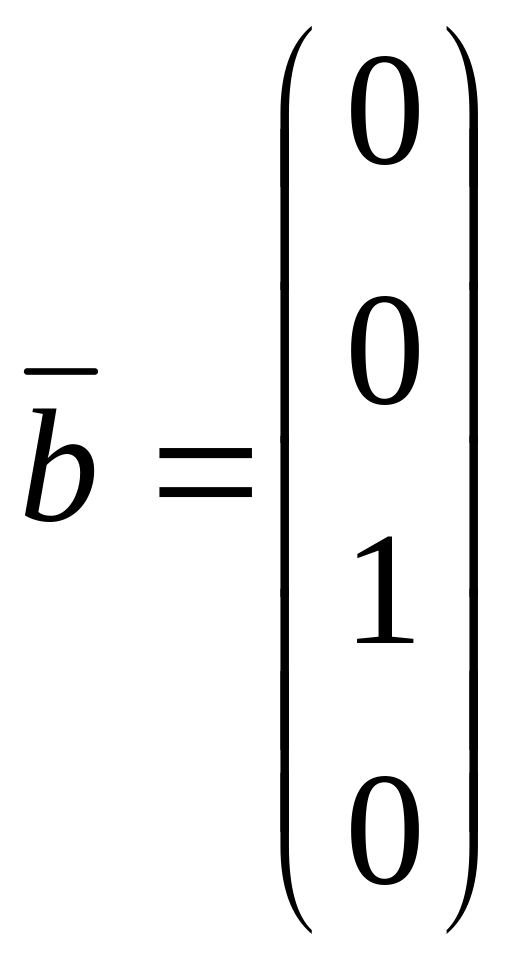 ,
,
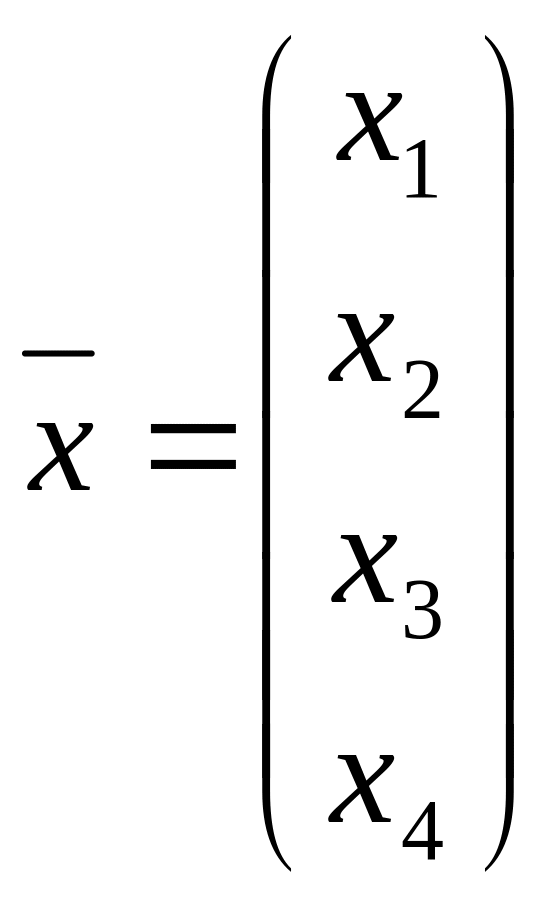 .
.
Решение
Составим систему уравнений:
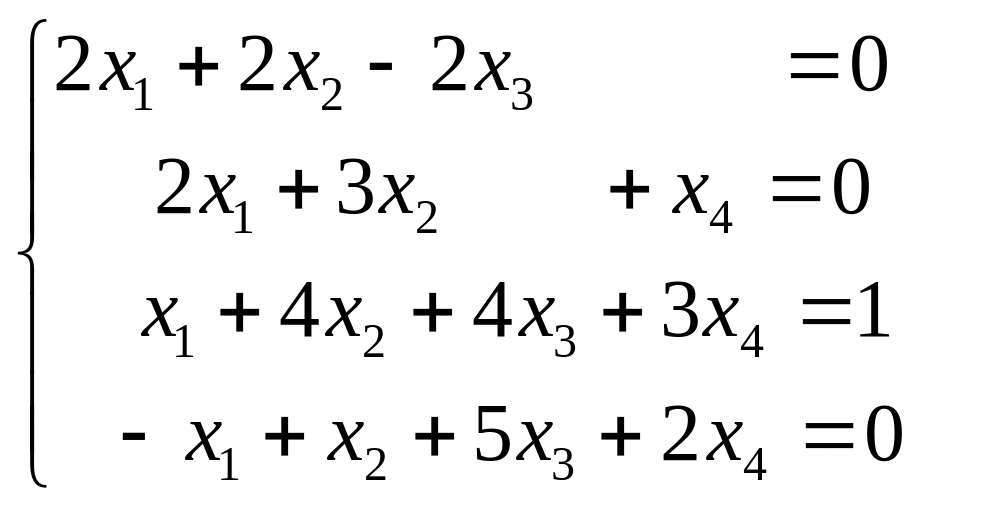 .
.
Вычислим
![]()
![]() =
=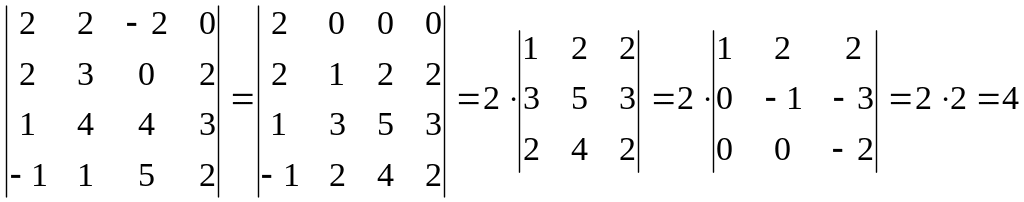
(из элементов второго столбца вычли элементы первого, а к элементам третьего столбца прибавили элементы первого, затем разложили по элементам первой строки).
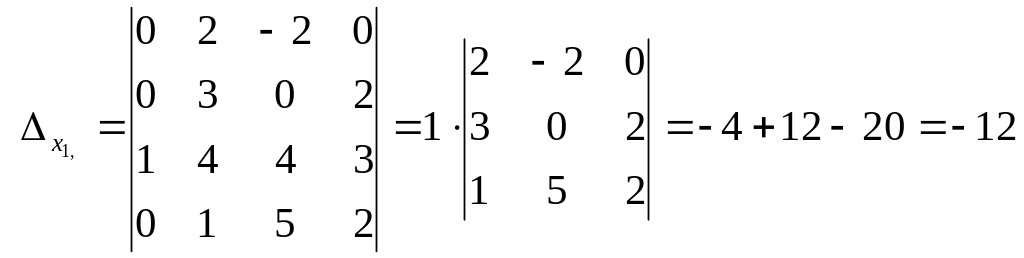
(разложили по элементам первого столбца).
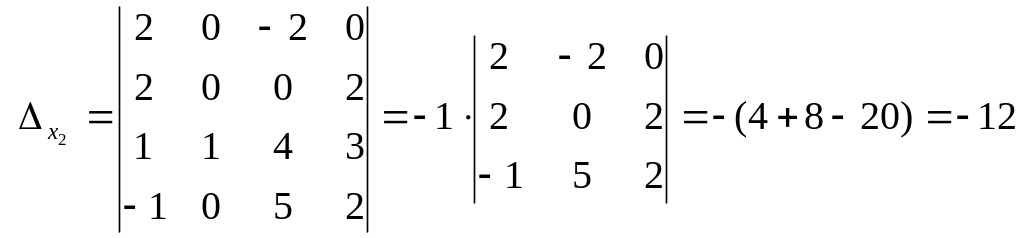
(разложили по элементам второго столбца).
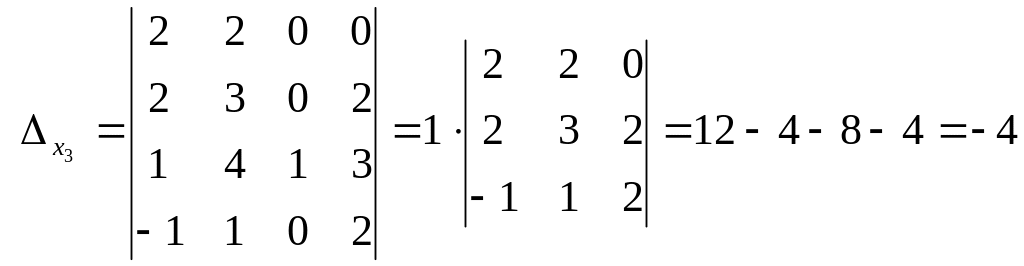
(разложили по элементам третьего столбца).
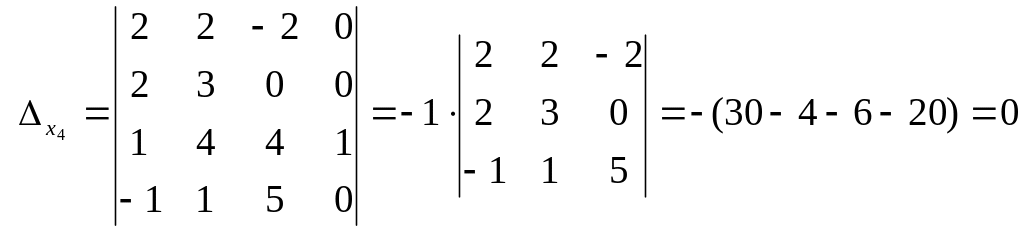
(разложили по элементам четвёртого столбца).
Применяя теперь формулы Крамера, получим
![]()
Задача 4
Исследовать системы
![]() на совместность. Совместные системы
решить методом Гаусса.
на совместность. Совместные системы
решить методом Гаусса.
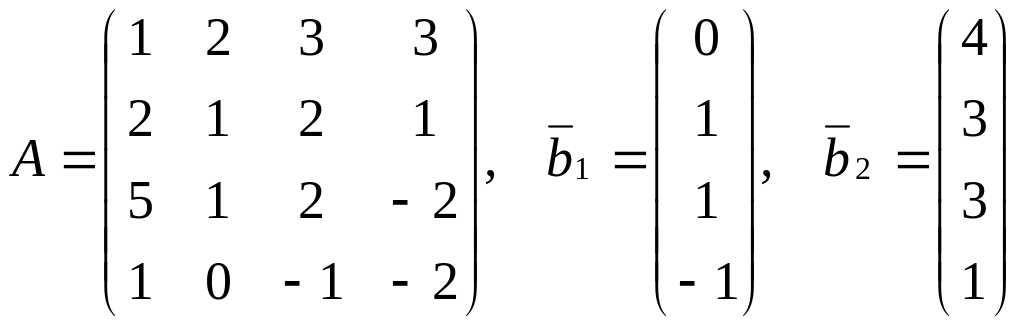 ,
.
,
.
Решение
1 Способ
Составим расширенную матрицу исходных систем:
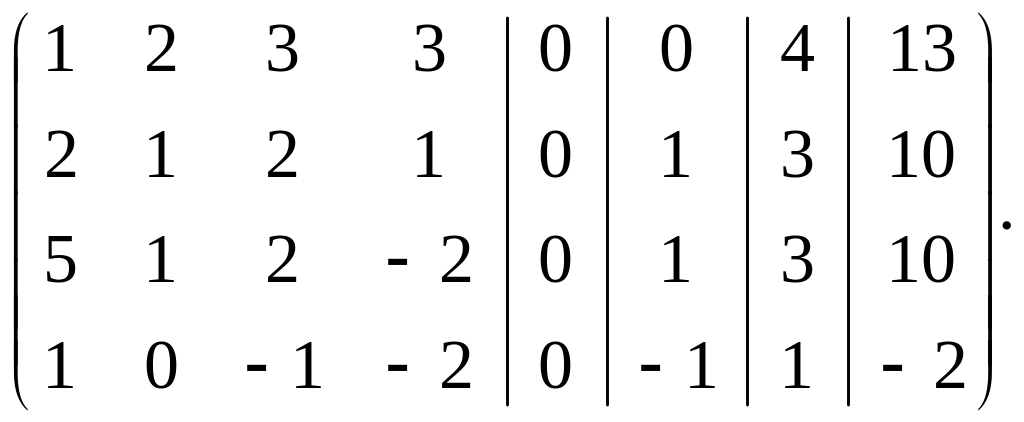
Последний столбец здесь является контрольным, каждый его элемент представляет собой сумму элементов соответствующей строки.
Например, 13=1+2+3+3+4 – сумма элементов первой строки.
Далее, производя элементарные преобразования, приводим матрицу к трапециевидной форме:

![]()
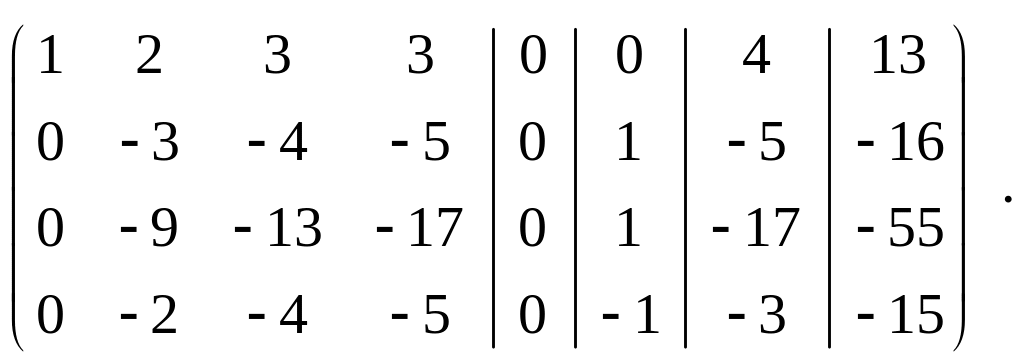
Последнюю матрицу получили, умножая первую строку сначала на (-2) и складывая со второй, затем на (-5) и складывая с третьей, затем на (-1) и складывая с четвёртой.
Теперь оперируем со второй строкой:
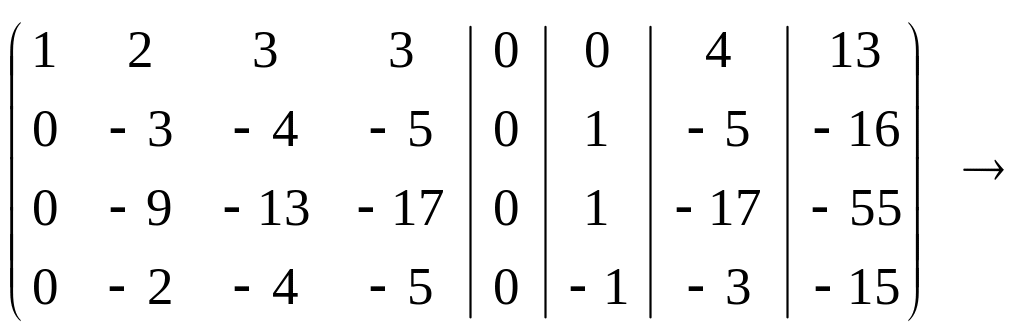
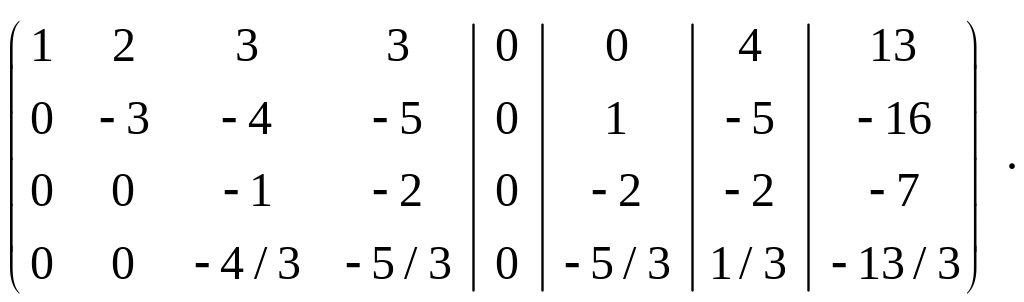
Последнюю матрицу получили, умножая вторую строку сначала на (-3) и складывая с третьей, затем на (-2/3) и складывая с четвёртой.
Теперь оперируем с третьей строкой:
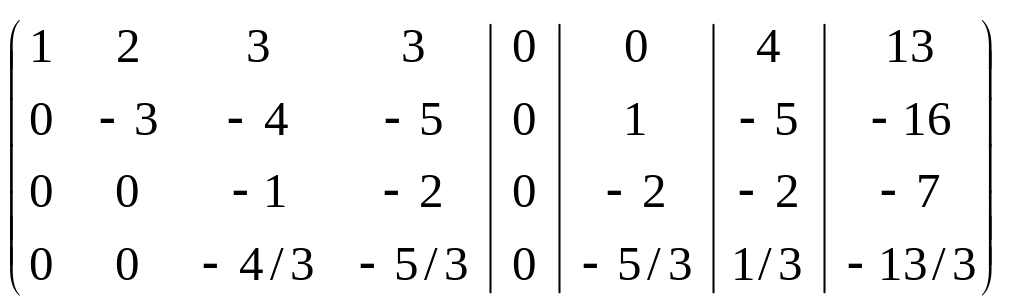
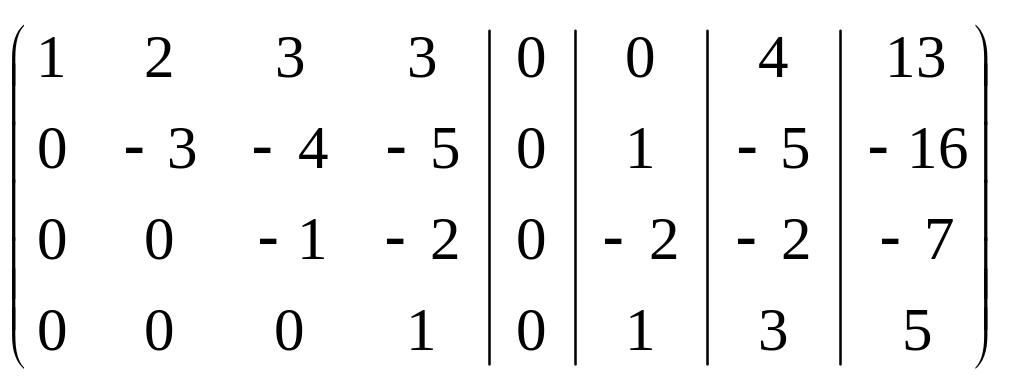 .
.
Последнюю матрицу получили, умножая третью строку на (-4/3) и складывая с четвёртой. Этой матрице соответствуют три системы:
1.
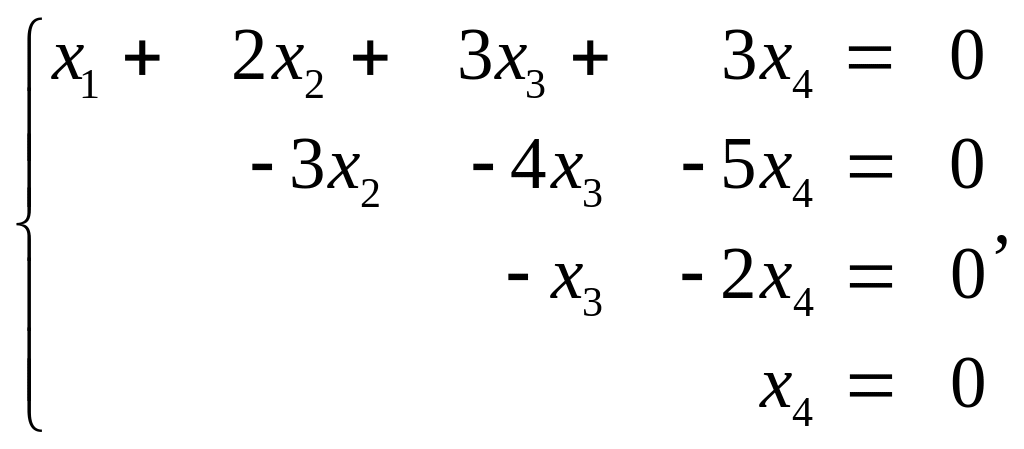
![]() 2.
2.
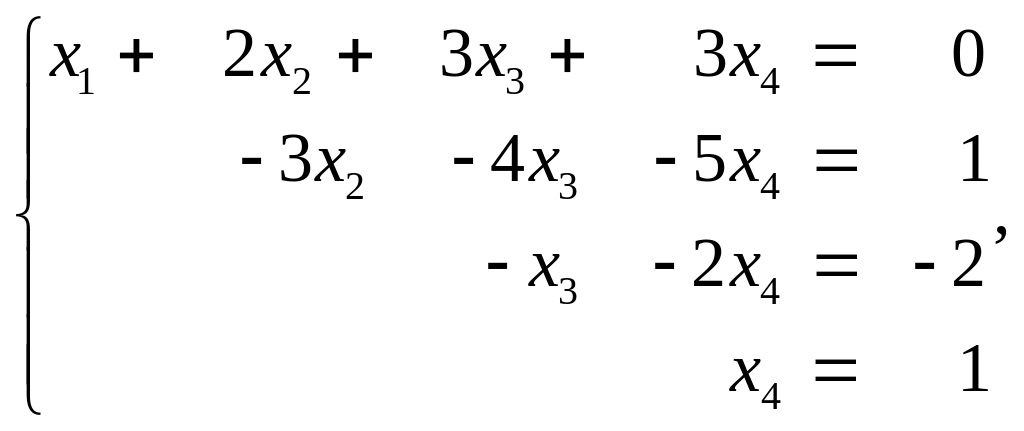
3.
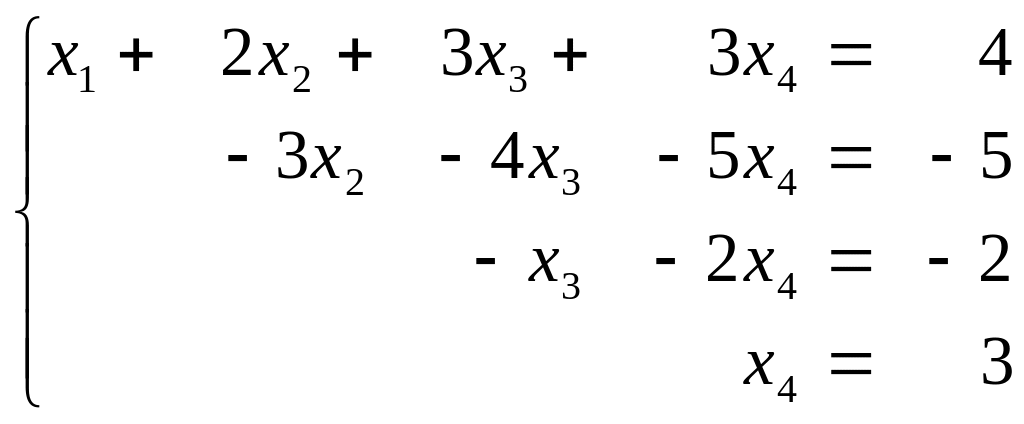 .
.
Решения этих систем: 1) (0,0,0,0);
2) (1,-2,0,1):
3) (3,2,-4,3).
2 Способ
Составим расширенную матрицу и приведём её к трапециевидной форме:
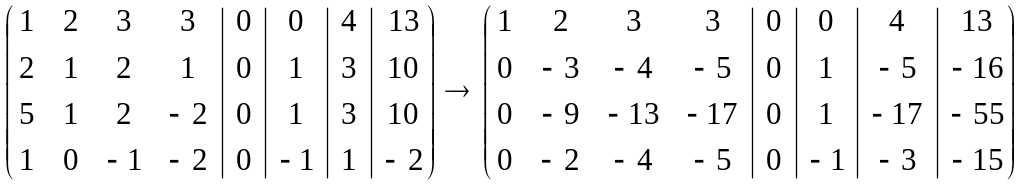 .
.
Последнюю матрицу получили, вычитая из элементов второй строки элементы первой, умноженные на 2; из элементов третьей – элементы первой, умноженные на 5; из элементов четвёртой вычитая элементы первой.
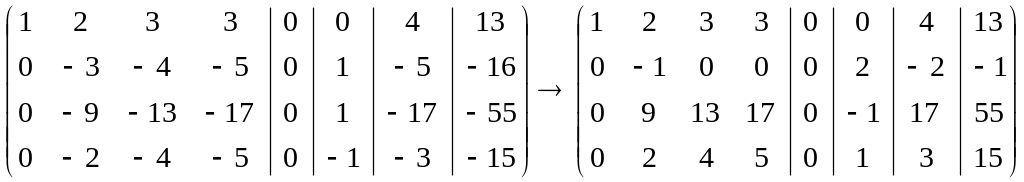 .
.
Последнюю матрицу получили, вычитая из элементов второй строки элементы четвёртой; умножая третью и четвёртую строки на (-1).
 .
.
Матрицу справа получили, умножив вторую строку на (-1); складывая третью строку со второй, умноженной на 9; четвёртую строку со второй, умноженной на 2.
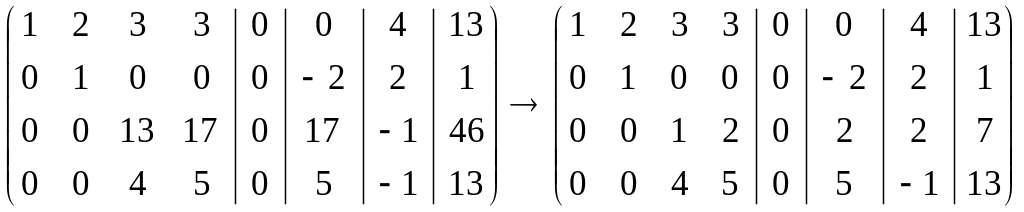 -
-![]()
матрицу справа получили, вычитая из третьей строки элементы четвёртой, умноженные на 3.
Теперь умножаем третью строку на (-1) и складываем с четвёртой:
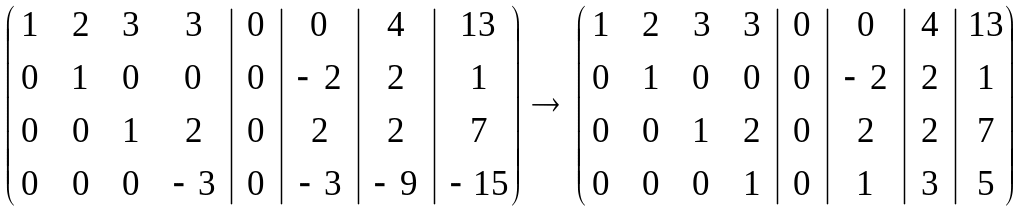 -
-
матрицу справа получили, разделив элементы четвёртой строки на (-1).
Этой матрице соответствуют три системы:
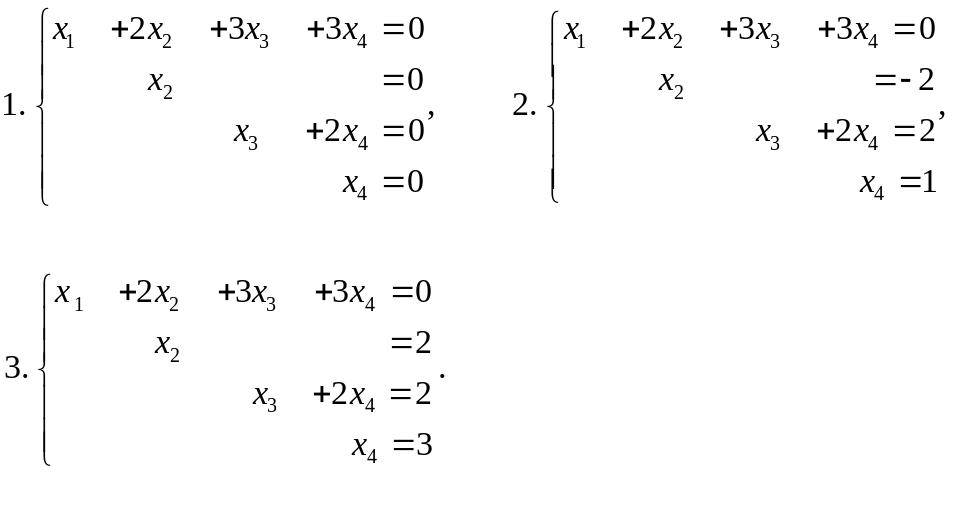
Решения этих систем: 1) (0, 0, 0, 0);
2) (1, -2, 0, 1);
3) (3, 2, -4, 3).
Задача 5
Найти собственные значения и собственные
векторы матрицы
![]()
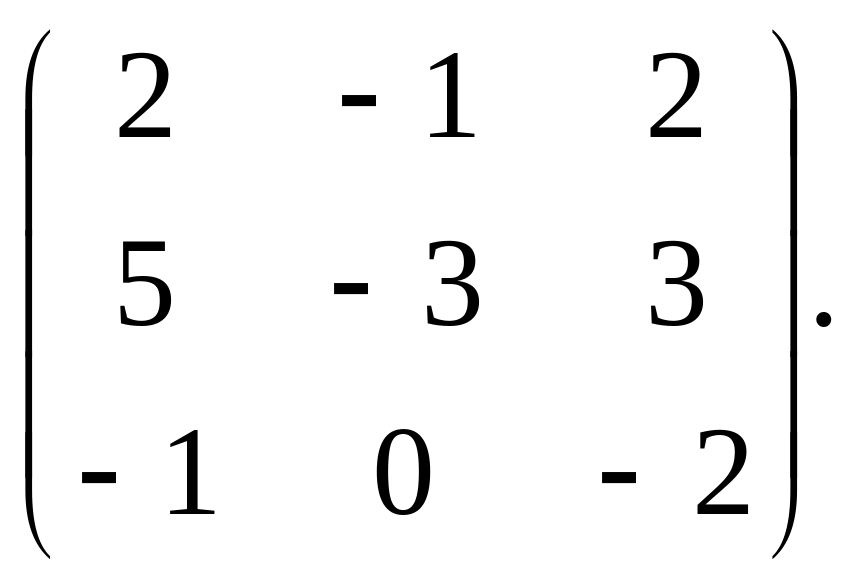
Решение
Составим характеристическое уравнение
![]()
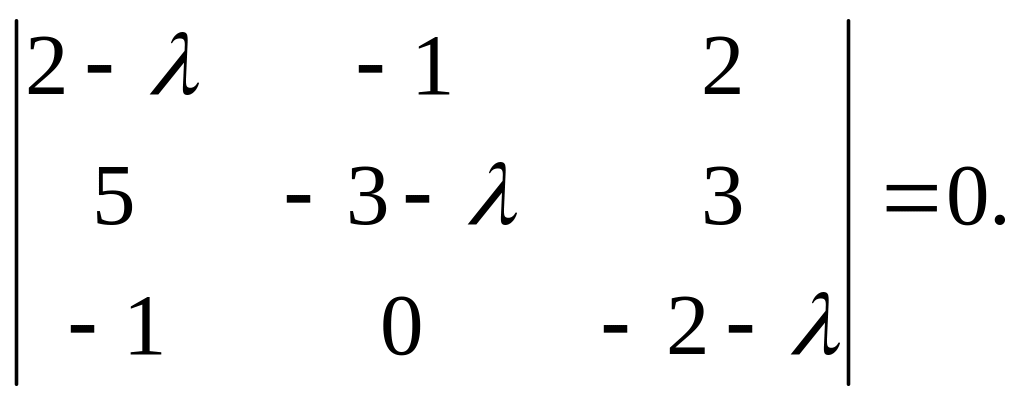
Отсюда, раскрывая определитель, имеем
![]()
Таким образом, собственные значения данного линейного преобразования
![]()
Найдём теперь собственный вектор
![]() .
Подставив значение
.
Подставив значение
![]() в уравнение
в уравнение
![]() ,
получим
,
получим
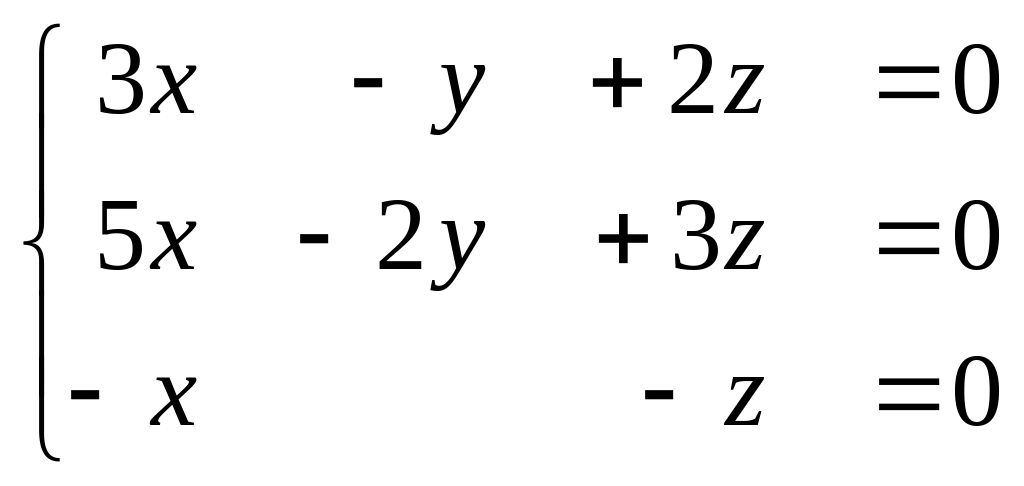 .
.
Отсюда
![]() Тогда
Тогда
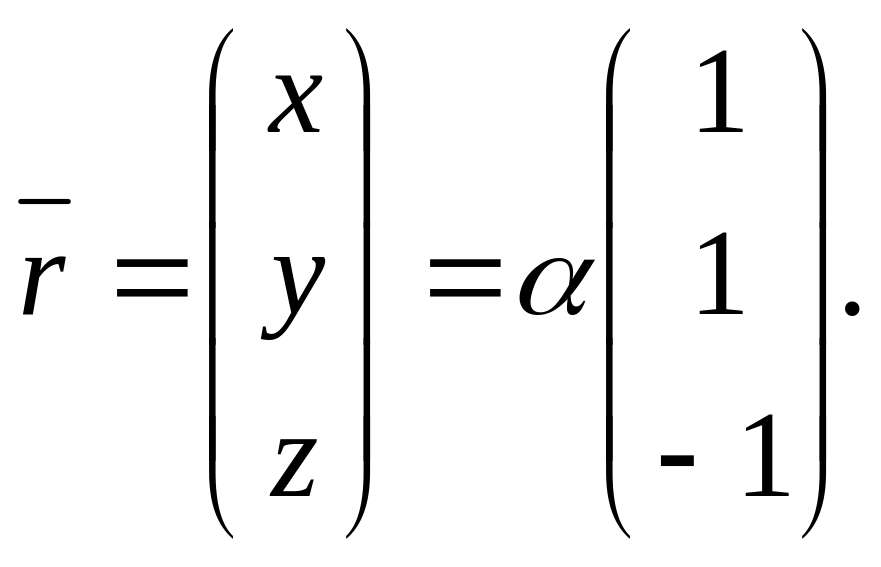
Задача 6
Привести уравнение кривой второго порядка к каноническому виду, сделать чертёж:
![]() .
.
Решение
Группа старших членов данного уравнения
образует квадратичную форму
![]() Её
матрица
Её
матрица
![]() .
Собственными значениями соответствующего
линейного преобразования будут числа
.
Собственными значениями соответствующего
линейного преобразования будут числа
![]() и
и
![]() (см. задачу 5). Следовательно, квадратичная
форма
(см. задачу 5). Следовательно, квадратичная
форма
![]() преобразуется к каноническому виду
преобразуется к каноническому виду
![]() ,
,
а данное уравнение – к виду
![]()
или
![]() .
.
Данная линия – эллипс (см. рис.1).
Можно указать и базис, в котором уравнение эллипса принимает канонический вид. Его легко получить, исходя из собственных векторов линейного преобразования с матрицей :
![]()
Нормируя векторы
![]() и
и
![]() ,
получим векторы
,
получим векторы
![]() и
и
![]() .
.
Базис
![]() ,
,
![]() и будет искомым ортонормированным
базисом, в котором данное уравнение
принимает канонический вид.
и будет искомым ортонормированным
базисом, в котором данное уравнение
принимает канонический вид.
Запишем теперь формулы преобразования
координат. Если обозначить векторы
исходного базиса
![]() и
и
![]() ,
то
,
то
![]() .
.
Здесь коэффициенты разложения представляют
собой направляющие косинусы вектора
,
т.е.
![]() .
Тогда уравнения связи новых и старых
координат имеют вид:
.
Тогда уравнения связи новых и старых
координат имеют вид:
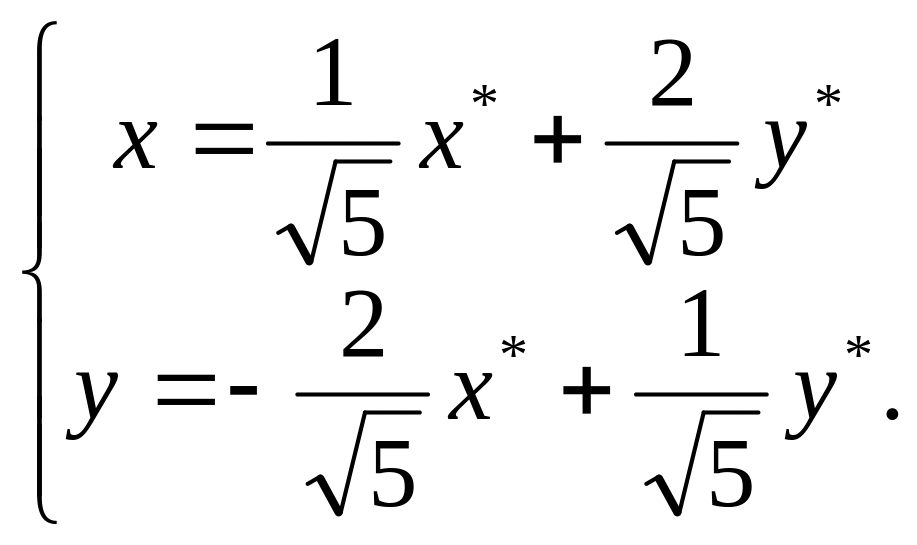
Если подставим эти выражения в данное уравнение, то, преобразовав его, убедимся, что будет получено то же каноническое уравнение.
![]()
![]()
![]()



 -2
-2



1
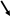
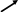

 00
00
00
00
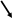



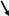

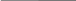

![]()

 -1
----1
-1
----1

![]()
2
![]()
Рис. 1
Условия задач типового расчёта
