1. Уравнение шредингера и элементы квантовой теории

1.1. Экспериментальные основания квантовой механики

К концу XIX века было практически закончено построение физики на базе классической механики Ньютона. Однако уже в самом начале ХХ века классическая физика столкнулась с трудностями при описании ряда явлений, которые либо не принимались ранее во внимание, либо были неизвестны. Одним из таких явлений стала так называемая «ультрафиолетовая катастрофа». Классическая теория излучения предсказывала концентрацию энергии излучения в области высоких частот, в то время как экспериментальные данные показывали обратное — энергия излучения уменьшалась с ростом частоты. Другим экспериментальным фактом, не нашедшим объяснения в рамках классической физики, стал дискретный (линейчатый) спектр излучения молекул и атомов, что невозможно было объяснить, используя классическую теорию движения применительно к электронам в атомах.

Практически все спектры излучения линейчатые, например знаменитая серия Бальмера для водорода, когда длины волн излучаемого света имеют только дискретные значения. Этим свойством обладают спектры излучения всех атомов. Частота излучения описывается формулой

где m — целое число, определяющее номер серии, , 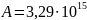1/c.

М. Планк устранил противоречие опыта и теории исходя из предположения о дискретной природе света, вводя минимальную порцию излучаемой или поглощаемой энергии излучения — квант света. При этом указанные процессы осуществляются дискретными порциями с энергией , где 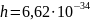Дж∙с — постоянная Планка.

Для описания дискретной природы излучения атомов Н. Бор (1913 г.) постулировал наличие разрешенных (дискретных) уровней энергии атома, что позволило объяснить экспериментальные линейчатые спектры. При этом переход атома из состояния m в состояние k сопровождается поглощением или излучением энергии

Таким образом, наряду с тем, что излучение обладает свойствами, описываемыми классической теорией (электродинамикой), такими как, например, дифракция, целый ряд фактов обнаруживает и дискретные свойства света, присущие частицам. А. Эйнштейн предложил концепцию фотона — частицы, составляющей свет. При этом энергия фотона в соответствии с формулой Планка есть . Экспериментальные измерения светового давления, выполненные П. Н. Лебедевым, позволили заключить о наличии у фотонов механического импульса , где λ — длина волны излучения.

Экспериментальная физика обнаружила и новые свойства «обычных» частиц, которые при определенных условиях проявляют волновые свойства. Например, при пропускании электронов через тонкий лист бериллия возникают дифракционные кольца, аналогичные картине, характерной для видимого света при его прохождении через малое отверстие. Аналогичный эффект наблюдается при прохождении нейтронов сквозь кристаллы. Предполагая у частиц наличие волновых свойств Л. Де-Бройль предложил характеризовать их длиной волны (длина волны Де-Бройля)

где m, v — масса и скорость частицы. При этом волновые свойства, в частности в упомянутых опытах, будут проявляться при взаимодействии частиц с объектами, размеры которых сравнимы с длиной волны. Поэтому дифракционные явления, связанные с прохождением пучков частиц через вещество, возникают, если длина волны Де-Бройля частиц в пучке соизмерима с расстоянием между атомами данного вещества.

Рассмотрим примеры. Макрочастица массой кг, движущаяся со скоростью 1000 м/с (дробинка вылетающая из ружья при стрельбе), имеет длину волны Де-Бройля м и, следовательно, не может проявлять волновых свойств в процессе своего движения. Электрон в твердом теле с характерным расстоянием между атомами нм при энергии 10 эВ имеет длину волны Де-Бройля нм и, следовательно, обнаруживает волновые свойства подобно описанному выше опыту с бериллиевой фольгой.

Таким образом, при описании мира на микроуровне следует принимать во внимание волновые свойства частиц.