2.4. Статистическая теория идеального газа

Вновь обратимся к формулам для заселенности квантовых состояний, полученным в предыдущем разделе. Оба результата можно представить, как мы это сделали в последнем выражении в виде

Из графиков обеих функций (рис. 15) видно, что при больших значениях энергии оба квантовых распределения перестают отличаться друг от друга. Такой режим называется классическим.

Идеальный газ определяется как система свободных невзаимодействующих атомов, находящихся в классическом режиме.

Модель идеального газа оказывается весьма плодотворной для целого ряда приложений, включая, газоразрядную плазму, течения и ударные волны в газовых средах.

Отсутствие потенциального взаимодействия между частицами идеального газа обуславливает лишь один вид энергии, присущей частицам составляющим газ — кинетическую энергию поступательного движения 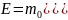. Как было сказано выше, в классическом режиме квантовые распределения перестают отличаться друг от друга, следовательно, единицей в знаменателе (35) можно пренебречь. В результате имеем

Поскольку , , 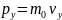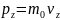последнее выражение приводится к виду

где

Формула (36) есть не что иное, как известная функция распределения частиц по скоростям Максвелла. Она дает число частиц в единице объема, обладающих скоростью из интервала

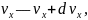
Постоянную в (36) можно найти, если задаться концентрацией частиц идеального газа (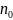 ) — полным числом частиц в единице объема. Тогда, интегрируя (36) слева и справа, получим

В качестве пределов интегрирования по скоростям в правой части можно выбрать интервалы . Несмотря на то, что всякая скорость не может превосходить скорость света, использование бесконечных скоростей в правой части последнего выражения не приведет к ошибке, так как оно содержит быстро затухающую функцию скорости. Принимая во внимание, что слева в последней формуле стоит интеграл от полного дифференциала, и разбивая экспоненту в правой части на три сомножителя, получим

Правая часть получившегося выражения содержит произведения трех одинаковых интегралов типа

Для вычисления этого интеграла найдем вначале :

Объединяя произведение интегралов в один интеграл по площади в координатах , , получим

Поскольку это интеграл по всей плоскости , , удобно перейти от декартовых координат к полярным с центром в точке , 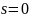, при этом радиальная координата ρ связана с декартовыми , , соотношением , а элемент площади интегрирования равен . В результате получим

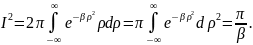
Теперь . Используя этот результат, вычислим правую часть (38)

Отсюда найдем постоянную

а распределение Максвелла по скоростям получит свой окончательный вид

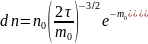
Распределение Максвелла можно использовать для нахождения средних значений величин, зависящих от скорости частицы. Пусть имеется некоторая функция скорости , тогда ее среднее значение будет найдено по формуле

Рассчитаем в качестве примера среднее значение квадрата скорости . При этом получим

Получившийся интеграл представляет собой интеграл по бесконечному объему в пространстве скоростей. При этом интегрируемая функция зависит только от , следовательно, обладает сферической симметрией по отношению к точке . Поэтому для интегрирования удобно использовать сферические координаты, в которых радиальная координата есть , а элемент объема

Теперь задача расчета среднего значения квадрата скорости частиц сводится к вычислению интеграла

Для вычисления интеграла в правой части выражения воспользуемся следующим приемом. Ранее мы нашли

Отсюда имеем в силу четности подынтегральной функции

Дважды продифференцируем полученное выражение по :

Таким образом, интеграл в правой части (40) найден, а искомая средняя величина квадрата скорости составит

Аналогичным путем можно найти среднее значение модуля скорости :

Для вычисления интеграла в правой части можно использовать новую переменную .

Заметим, что среднеквадратичная скорость и полученная здесь средняя скорость отличатся множителем 1,178, т. е. практически равны. В следующем разделе будет показано, что энергетическая температура связана с термодинамической соотношением , где Дж/K. Поэтому приведенные формулы можно применять для вычисления тепловой скорости частиц в газах. В частности для кислорода ( кг – масса молекулы) при комнатной температуре  K, средняя тепловая скорость составит 480 м/с.