Возникновение и исчезновение возбужденных состояний

Мы установили, что при поглощении атомом энергии возможно возбуждение — переход электронов в состояния с более высоким уровнем энергии. Вместе с тем энергетически допустим и обратный процесс с учетом правила отбора. Предельный случаи возбуждения достигается, когда электрон получает энергию достаточную для перехода в свободное состояние. В этом случае происходит ионизация атома: возникают две свободные заряженные частицы —  положительный ион и электрон, обладающий отрицательным зарядом. Рассмотрим, какими конкретными путями реализуются эти процессы. Возбуждение (ионизация) возможна при следующих неупругих столкновениях первого рода:

1. Столкновения атомов друг с другом. Часть кинетической энергии атомов может быть передана электрону, который перейдет на более высокий энергетический уровень. Явление характерное при термической ионизации газа, когда температура, достигает нескольких тысяч градусов.

2. Столкновение атома со свободным электроном. Часть энергии свободного электрона может быть передана электрону из оболочки атома, в результате последний переходит на более высокий уровень. Процесс характерен для газа, находящегося в сильном электрическом поле, когда свободный электрон может быть достаточно ускорен электрической силой.

3. Взаимодействие электромагнитного излучения с электронной оболочкой атома. В случае газов процесс имеет место при любых условиях.

Вместе с тем возможны и столкновения второго рода, при которых атом теряет энергию:

1. Атом при переходе в основное состояние передает энергию медленному свободному электрону.

2. При столкновении возбужденного атома с атомом, находящимся в основном состоянии, первый возвращается в основное, а второй — в возбужденное состояние. Этот процесс особенно эффективен (носит резонансный характер), если соответствующие энергии возбуждения атомов близки, например, в гелий-неоновой смеси.

3. При взаимодействии возбужденного атома с излучением. В этом случае воздействие кванта излучения на возбужденную электронную оболочку вызывает переход электрона на более низкий уровень и излучение нового кванта — вынужденное излучение.

1.7. Многоэлектронные квантовые системы

При переходе к системам с двумя или большим количеством частиц, например, электронов, появляются некоторые новые факты, отражаемые в квантовомеханических постулатах, которые вытекают из эксперимента.

Главным постулатом является принцип неразличимости одинаковых по своей природе частиц. Если две частицы находятся на расстоянии, когда их волновые пакеты перекрываются, т. е. на расстоянии порядка длины волны Де-Бройля, то нельзя говорить, что частица 1 находится в окрестности точки , а частица 2 в окрестности точи , а можно лишь указать, что две частицы находятся в окрестностях точек и . В качестве примера рассмотрим систему, состоящую из двух частиц 1 и 2, которые могут принимать значения энергии и . С точки зрения классической физики в такой системе может быть два состояния: 1) частица 1 имеет энергию , частица 2 — энергию ; 2) частица 1 обладает энергией , а частица 2 — энергией . При действии принципа неразличимости частиц описанные два состояния являются одним и тем же состоянием.

Математически принцип неразличимости можно выразить следующим образом. Пусть движение двух частиц описывается волновой функции 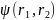. При этом является плотностью вероятности обнаружения частиц в окрестностях точек 1 и 2. Но в силу принципа неразличимости частиц эта функция не должна изменятся при перестановке аргументов местами (теперь первую частицу помещаем в положение 2, а вторую — в положение 1. При этом получим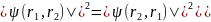 . Отсюда следует

.

В случае знака «+» в последнем соотношении волновая функция называется симметричной, в случае «–» — антисимметричной. Если две частицы совершают одномерное движение вдоль оси x, волновая функция должна удовлетворять соотношению

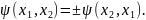
Например, функция является симметричной, а функция  — антисимметрична.

Второй факт, характеризующий поведение квантовой системы из многих частиц, имеющий место независимо от принципа неразличимости, — обменное вырождение. Напомним, что вырождением называется явление, когда одно и то же значение энергии системы, реализуется при различных квантовых состояниях (наборах квантовых чисел). В качестве примера рассмотрим две частицы, совершающие одномерное движение вдоль оси x в потенциальной яме с бесконечно высокими стенками. Потенциальную функцию систему двух частиц при этом можно представить в виде

где 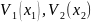 — индивидуальные потенциальные функции частиц,  — потенциал взаимодействия между частицами. Стационарное уравнение Шредингера для двух частиц можно в общем виде записать, как

При одномерном движении , . Рассмотрим две невзаимодействующие частицы в одномерной потенциальной яме с бесконечно высокими стенками. При этом . Тогда уравнение Шредингера получит вид

Будем искать решение данного уравнения в виде произведения двух функций, каждая из которых зависит только от одной переменной . Подставляя данное представление в предыдущее уравнение и деля на , получим

Если неизвестную постоянную (энергию) представить в виде суммы двух констант , то последнее уравнение можно представить в виде суммы двух независимых уравнений

Решение каждого из этих уравнений нам хорошо известно по задаче о движении одной частицы в одномерной потенциальной яме (раздел 1.2):

, ,

, ,

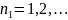
Отсюда найдем решение исходного уравнения

Квантовые числа и отличаются друг от друга. Разные комбинации квантовых чисел соответствуют разным квантовым состояниям системы. При этом энергия системы при различных комбинациях квантовых чисел, например , и 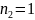, , может оставаться одной и той же. Следовательно, такой энергетический уровень системы является вырожденным. В общем случае, если первая находится в квантовом состоянии с числом , а вторая в состоянии , то при перемене частиц местами (частица 1 в состояние , а частица 2 в состояние ) мы формально получаем новое квантовое состояние и волновая функция системы изменится с на (энергия при этом не изменилась). Выше мы получили, что для выполнения принципа неразличимости квантовых частиц необходимо, чтобы волновая функция была либо симметрична, либо антисимметрична. Из записанной здесь пары решений можно построить линейную комбинацию, которая данному свойству удовлетворяет, и как любая суперпозиция решений, также является решением исходного уравнения:

При этом знак «+» соответствует симметричной волновой функции, «–» — антисимметричной. Постоянную α находим с помощью условия нормировки

Подставляя последнее выражение для 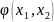под знак интеграла, найдем

Поскольку волновые функции и удовлетворяют условию нормировки, то первые два слагаемых в квадратных скобках дают в сумме 2. Третье слагаемое в скобках содержит интегралы от произведения разных волновых функций и в силу свойства ортогональности последних равно нулю. Поэтому получим . Откуда и

Частицы, обладающие в системе антисимметричной волновой функцией, называются фермионами. К фермионам относятся частицы с дробным спином, проекция которого принимает значения 1/2, 3/2 и т. д. Частицы с целыми значениями проекции спина 0, 1, 2 и т. д. — бозоны, обладающие симметричной волновой функцией. Фермионами в частности являются электроны, протоны, нейтроны. К бозонам относятся фотоны, дейтоны и другие частицы, содержащие четное число фермионов.

Обратим внимание на то, что волновая функция двух фермионов

может быть вычислена как определитель

Нетрудно обобщить эту формулу на случай произвольного числа N фермионов

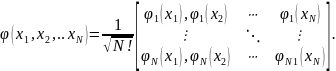
Если предположить, что какие-либо 2 из N фермионов находятся в одинаковых квантовых состояниях, то это будет означать равенство всех элементов соответствующих строк в выписанном определителе. Например, если первый и N-ый фермионы пребывают в одном квантовом состоянии, то первая и последняя строки определителя равны друг другу. По свойству определителей, определитель, имеющий хотя бы две одинаковые строки, тождественно равен нулю. Таким образом, волновая функция системы фермионов, в которой хотя бы два находятся в одинаковом квантовом состоянии, тождественно равна нулю. Следовательно, такое состояние не реализуемо. Полученный результат в отношении системы фермионов фактически формулирует математически известный принцип запрета Паули для электронов.