2.1.3. Решение задачи линейного программирования средствами Excel

Рассмотрим решение задач линейного программирования средствами Excel сначала в общем виде с наиболее общими рекомендациями, а затем – решение частных задач.

Ссылка указывает на ячейку или диапазон ячеек листа и передает в Microsoft Excel сведения о расположении значений или данных, которые требуется использовать в формуле. При помощи ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать в нескольких формулах значение одной ячейки. Кроме того, можно задавать ссылки на ячейки других листов той же книги, на другие книги, а также на данные других приложений. Ссылки на ячейки других книг называются внешними. Ссылки на данные других приложений называются удаленными.

Различия между относительными и абсолютными ссылками. Относительные ссылки. При создании формулы ссылки обычно учитывают расположение относительно ячейки, содержащей формулу. В следующем примере ячейка B6 содержит формулу =A5; искомое значение находится на одну ячейку выше и левее ячейки B6. Такая ссылка называется относительной. При копировании формулы с относительными ссылками Excel автоматически изменяет ссылки во вставляемой формуле для указания на другие ячейки в соответствии с положением формулы. В приведенном ниже примере формула в ячейке B6 (=A5), которая ссылается на ячейку, расположенную на одну строку выше и на один столбец левее, скопирована в ячейку B7. Excel изменил формулу в ячейке B7 на =A6, ссылаясь на ячейку, которая расположена на одну строку выше и на один столбец левее ячейки B7.

Абсолютные ссылки. Если необходимо, чтобы ссылки не изменялись при копировании формулы в другую ячейку, воспользуйтесь абсолютными ссылками. Например, если имеется формула, умножающая содержимое ячейки A5 на ячейку C1 (=A5*C1), то при копировании формулы в другую ячейку изменятся обе ссылки. Для создания абсолютной ссылки на ячейку C1, поставьте знак доллара ($) перед той частью ссылки, которая не должна изменяться. Чтобы создать абсолютную ссылку на ячейку C1, поместите знак доллара так, как показано в примере: =A5*$C$1.

Относительные и абсолютные ссылки. В зависимости от выполняемых задач в Excel можно использовать относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, или абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например, $A$1, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при их копировании, а абсолютные ссылки − нет.

Теперь рассмотрим общее решение задачи. На листе введите данные к задаче (рис. 1.1).

Рис. 1.1.

Ячейки B2:B4 предназначены для значений изменяемых переменных. В ячейки C2:E5 вводим условия задачи, в ячейку B7 формулу для вычисления целевой функции. Для решения задачи воспользуйтесь надстройкой MS Excel Поиск решения. Раскройте пункт меню Сервис, выберите команду Поиск решения. (Если в меню Сервис отсутствует команда Поиск решения, загрузите эту надстройку: Выберите команду Сервис-Надстройки и активизируйте надстройку Поиск решения.)

Рис. 1.2.

Появится диалоговое окно Поиск решения (рис. 1.2). В нем есть три основные параметра: • установить целевую ячейку; • изменяя ячейки (т.е. ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат целевой ячейки. К изменяемым ячейкам предъявляются два основных требования: они не должны содержать формулы и их изменение должно отражаться на результаты в целевой ячейке); • ограничения (правила, которыми Поиск решения будет руководствоваться для нахождения правильного ответа). Сначала заполните поле Установить целевую ячейку − B7. Затем установите переключатель равной максимальному значению. Наконец, определите данные поля Изменяя ячейки, выделив ячейки B2:B4. Теперь определите ограничения: щелкните на кнопке Добавить. Появится диалоговое окно Добавление ограничения (рис. 1.3). Введите ограничения на неотицательность переменных $B$2:$B$4 >=0 и щелкните на кнопке Добавить.

Рис. 1.3.

Введите также ограничения на количество используемого сырья: $F$2<=$G$2, $F$3<=$G$3, $F$4<=$G$4

В результате диалоговое окно Поиск решения принимает вид рис. 1.4.

Кнопка Параметры позволяет настроить параметры модели (рис. 1.5). Теперь для процедуры Поиска решения готовы все исходные данные. Чтобы начать процесс решения задачи, щелкните на кнопке Выполнить. В строке состояния будет отражаться ход решения задачи.

Через некоторое время на экране появится диалоговое окно Результаты поиска решения (рис. 1.6), в котором вы можете выбрать одну из следующих возможностей: • сохранить найденное решение; • восстановить исходные значения в изменяемых ячейках; • создать несколько видов о процедуре поиска. Установите переключатель Сохранить найденное решение и щелкните на кнопке ОК.

В итоге получите требуемое решение − необходимое количество каждого вида напитков и величину максимальной при этом прибыли: в ячейках B2:B4 найдены значения переменных x₁ = 0, x₂ = 8, x₃ = 20, в ячейке B7 значение целевой функции F = 400 (рис. 1.7).

Рис. 1.4.

Рис. 1.5.

Рис. 1.6.

Далее рассмотрим решение конкретной задачи линейного программирования средствами Excel на примере следующей задачи.

Найти оптимальное решение задачи линейного программирования:

.

Рис. 1.7.

Для решения этой задачи в Excel следует воспользоваться подпунктом Поиск решения пункта меню Сервис.

Предварительно введём в ячейку А4 формулу целевой функцию в следующем виде: =17*A1+43*A2+62*A3 (по аналогии с рис.1.1).

Значения в ячейках А1, А2 и А3 отведём под значения переменных x₁, x₂ и x₃ соответственно. Числовые значения переменных x₁, x₂ и x₃ в эти ячейки будут введены автоматически в процессе решения задачи.

В ячейки В1, В2 и В3 введём математические формулы ограничений в виде табл. 1.3.

Таблица 1.3

Математические формулы ограничений
Ячейка	Значение
В1	=2*А1+3*А2+7*А3
В2	=7*А1+7*А2+7*А3
В3	=8*А1+2*А2+7*А3

Затем введём в ячейки С1, С2 и С3 значения 480, 960 и 1000 соответственно, ограничивающие численные значения переменных задачи.

Таким образом, все исходные данные задачи записаны в том виде, в котором они используются в окне Поиск решения.

Теперь воспользуемся подпунктом меню Excel Поиск решения.

На экране появится следующее окно (см. рис. 1.2):

В поле Установить целевую ячейку указываем ячейку А4. Решение ищем для максимального значения, что указывается переключателем поля Равной, установленным на записи со словами «максимальному значению».

В поле Изменяя ячейки указываем диапазон изменения ячеек от А1 до А3, а именно $A$1:$A$3.

Для приведения в рабочее состояние математической программы поиска оптимального решения заданной задачи необходимо установить ограничения, учитываемые при её решении. Для этого нажимаем на кнопку Добавить, расположенную справа от поля Ограничения. На экране появляется следующее окно (рис. 1.8).

Рис. 1.8.

Для добавления первого ограничения, а именно , в поле Ссылка на ячейку указываем ячейку В1, затем в списке, расположенном посередине, выбираем знак «<=» и в поле Ограничение указываем ячейку С1. После этого нажимаем на кнопку Добавить. Аналогично добавляем два оставшиеся ограничения задачи. Закрываем окно, нажав на кнопку Отмена.

Окно Поиск решения примет вид, показанный на рис. 1.9.

Рис. 1.9.

Нажимаем на кнопку Параметры. Вместо предыдущего окна появится окно Параметры поиска решения, позволяющее выбрать параметры математического метода поиска решения; если есть необходимость в знании промежуточных результатов вычислений при поиске оптимального решения, нужно отметить пункт Показывать результаты итераций в открывшемся окне (рис. 1.5). В Excel в качестве методов поиска решения задачи предлагаются метод Ньютона и метод сопряженных градиентов. Для решения задач линейного программирования обычно используется метод Ньютона. Предельное число итераций, относительная погрешность и допустимое отклонение выбираются соответствующими той задаче, оптимальное решение которой находится. Максимальное время назначается по опыту решения аналогичных задач на используемом компьютере. Показанные установки в окне Параметры поиска решения на рис. 1.5, как правило, оказываются достаточными для получения оптимального решения задач линейного программирования.

В этом окне отмечаем «галочкой» пункты Линейная модель и Неотрицательные значения (последний на рисунке не показан). Нажимаем на кнопку ОК, после чего вновь появляется окно Поиск решения, и уже в окне Поиск решения нажимаем на кнопку Выполнить. Параметры в окне должны выбираться реальные, соответствующие заданным числовым характеристикам конкретной задачи. Увлечение большим числом итераций и малыми значениями относительной погрешности в производственных задачах может привести к необоснованному увеличению времени поиска решения.

На экран выводится окно Результаты поиска решения (рис. 1.6).

Нажатием на кнопку ОК закрываем окно. После этого в ячейках, отведённых для записи решения задачи, появляются числа (рис. 1.10).

Рис. 1.10.

В ячейке А4 находим значение целевой функции F(X), соответствующее найденному решению. В ячейках А1, А2 и А3 указаны соответствующие значения переменных x₁, x₂, x₃.

Для решаемой нами задачи оптимальное решение имеет следующий вид:

F = 6222,857, x₁ = 0, x₂ = 120 и x₃ = 17,14286.

Рассмотрим решение еще одной задачи, для которой в среде Exel используется приведенный выше алгоритм (для данной задачи применим собственную нумерацию). В настоящей задаче детально рассмотрим функцию Exel Отчет по результатам.

1. Ввод условий задачи.

1.1. Создание формы для ввода условий задачи. Форма для ввода условий задачи

.

,

,

,

имеет следующий вид

Ввод исходных данных. Заполняются ячейки, содержащие: нижние и верхние границы переменных, коэффициенты целевой функции, коэффициенты ограничений, знаки ограничений, направление оптимизации целевой функции.

2. Ввод зависимостей из математической модели. Заполняются ячейки содержащие: функцию, реализующую целевую функцию задачи, функции реализующие левые части ограничений задачи.

2.1. Ввод зависимости для целевой функции.

2.1.1. Поместить курсор в ячейку, отведенную под значение целевой функции.

2.1.2. Выбрать кнопку Мастер функций.

2.1.3. Выбрать в окне Категория категорию математические.

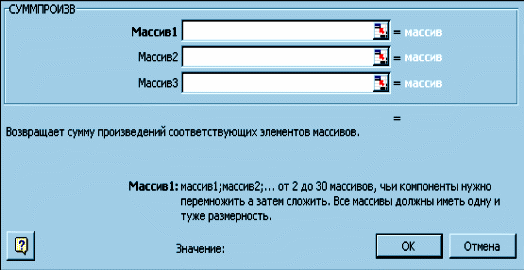
2.1.4. Выбрать функцию СУММПРОИЗВ (рис. 1.11).

Рис. 1.11.

2.1.5. Заполнить диалоговое окно функции СУММПРОИЗВ.

В массив 1 нужно занести диапазон ячеек, содержащих значения переменных (рис. 1.12) . В массив 2 – диапазон ячеек, содержащих коэффициенты целевой функции.

Рис. 1.12.

3.2. Ввод зависимостей для левых частей ограничений.

3.2.1. Поместить курсор в ячейку, отведенную под левую часть ограничения.

3.2.2. Выбрать кнопку Мастер функций.

3.2.3. Выбрать в окне Категория категорию математические.

2.1.6. Выбрать функцию СУММПРОИЗВ.

2.1.7. Заполнить диалоговое окно для функции СУММПРОИЗВ.

Занести в массив 1 диапазон ячеек, содержащих значения переменных (использовать при этом абсолютные ссылки), в массив 2 – диапазон ячеек, содержащих коэффициенты данного ограничения.

2.1.8. Копировать содержимое ячейки в буфер.

2.1.9. Вставить содержимое буфера в ячейки, от веденные под левые части остальных ограничений.

4. Ввод основных параметров модели в диалоговом окне Поиск решения.

4.3. Войт и в меню Сервис и выбрать пункт Поиск решения (рис. 1.13).

Рис. 1.13.

4.4. Заполнить параметры диалогового окна Поиск решения.

4.4.1. В пункте Установить целевую указать ячейку, отведенную под целевую функцию.

4.4.2. В соответствии с решаемой задачей выбрать направление целевой функции.

4.4.3. Нажать кнопку Добавить. Появится диалоговое окно для построения ограничений задачи. В левой части указывается ячейка (группа ячеек), в которой содержится левая часть ограничения, в центре – знак ограничения, в правой части – ячейка (группа ячеек) с правой частью ограничения. После ввода каждого ограничения нужно нажимать на кнопку Добавить. Когда все ограничения задачи построены, нужно нажать на кнопку Отмена и вернуться в диалоговое окно Поиск решения.

4.4.4. Нажать кнопку Параметры диалогового окна Поиск решения.

Появится диалоговое окно Параметры поиска решения (рис. 1.14).

С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. В ряде пунктов данного окна записаны значения, используемые по умолчанию. Команды, используемые по умолчанию, подходят для большей части практических задач. Команда Максимальное время служит для назначения времени в секундах, выделяемого на поиск решения задачи. В это поле можно ввести значение, не превышающее 32767 с (более 9 часов). Значение 100, используемое по умолчанию, подходит для решения большинства задач. Команда Предельное число итераций служит для назначения числа итераций.

4.4.5. Установить флажок Линейная модель. Это обеспечит применение симплекс-метода.

Рис. 1.14.

4.4.6. Нажать на кнопку Выполнить. Начнется решение составленной математической модели задачи. Через какое-то время появится диалоговое окно Результаты поиска решения (рис. 1.15).

Рис. 1.15.

Нужно выбрать интересующие виды отчетов по решению задачи и проанализировать полученное решение. Каждый из выбранных типов отчета создается на отдельном листе.

Отчет по результатам состоит из трех таблиц. Таблица 1 приводит сведения о целевой функции. В столбце Исходно при ведены значения целевой функции до начала вычислений. Таблица 2 приводит значения искомых переменных, полученные в результате решения задачи. Таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.

Отчет по устойчивости состоит из двух таблиц. В Таблице 1 при водятся следующие значения переменных: результат решения задачи; редуцированная стоимость, т. е. дополнительные двойственные переменные, которые показывают, насколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение; коэффициенты целевой функции; предельные значения приращения каждого коэффициента целевой функции, при которых сохраняется набор базисных переменных в оптимальном решении. В Таблице 2 приводятся аналогичные значения для ограничений: величина использованных ресурсов; теневая цена, т. е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу; значения приращения каждого ресурса, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.

Отчет по пределам показывает, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.

В качестве следующего примера рассмотрим решение одной из задач производственного планирования

Предприятие выпускает четыре вида продукции: Прод1, Прод2, Прод3, Прод4. Требуется определить, в каком количестве надо выпускать эти продукты, чтобы получить максимальную прибыль. Известно, что для изготовления данных продуктов требуются ресурсы трех видов: трудовые, сырьевые, финансы. Нормы расхода (количество ресурса каждого вида, необходимое для выпуска единицы продукции каждого типа), а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл. 1.4.

Таблица 1.4

Исходные данные к примеру

Математическая модель данной задачи имеет вид

.

;

;

;

.

1. Составим форму для данной задачи линейного программирования.

2. Введем зависимости из математической модели.

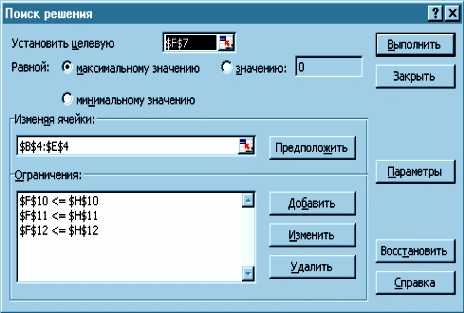
3. Вызовем диалоговое окно Поиск решения. В нем устанавливается целевая ячейка (F7), изменяемые ячейки (B3:E3), указывается направление поиска (максимизация). Далее выбирается команда Добавить и в появившемся диалоговом окне Добавление ограничения вводятся ограничения: F10<=H10, F11<=H11, F12<=H12 (рис. 1.16).

Условия неотрицательности переменных можно ввести в диалоговом окне Параметры поиска решения (см. рис. 1.14). В окне Параметры поиска решения устанавливается также флажок Линейная модель.

Рис. 1.16.

4. Запустим программу на выполнение из окна поиск решения. На экране появится диалоговое окно Результаты поиска решения. В данном диалоговом окне сделан вы вод о том, что найдено оптимальное решение (рис. 1.17).

Рис. 1.17.

Результат решения задачи приведен в следующем табличном виде:

Настоящая таблица показывает, что максимальная прибыль (F7=1320) будет достигнута предприятием при следующем выпуске продукции: прод1=B4=10, прод2=C4=0, прод3=D4=6, прод2=E4=0. В специально отведенных ячейках таблицы отражается количество использованных ресурсов: трудовых=F10=16, сырья=F11=84, финансов=F12=100.

5. Представим результаты решения задачи графически (рис. 1.18).

Рис. 1.18.

Проведем анализ полученного решения. Анализ решения осуществляется на основании трех видов отчетов, представленных в окне Результаты поиска решения: результаты, устойчивость, пределы. Начнем с Отчета по результатам (рис. 1.19). Данный отчет находится на отдельном листе. Отчет состоит из трех таблиц. Таблица 1 приводит сведения о целевой функции. В столбце Исходно приведены значения целевой функции до начала вычислений – 0, а в столбце Результат – значение целевой функции в оптимальном решении – 1320. Таблица 2 приводит значения искомых переменных, полученные в результате решения задачи. Таблица 3 показывает результаты оптимального решения для ограничений задачи: трудовые, сырье, финансы. В столбце Формула приведены ограничения в том виде, в котором они были введены в диалоговом окне Поиск решения, в столбце Значение приведены величины использованного ресурса.

Рис. 1.19.

Трудовые ресурсы использованы в количестве 16, сырье – 84, финансы – 100. В графе Разница показано количество неиспользованного ресурса. Трудовые ресурсы использованы полностью, остаток сырья составляет 26, финансы использованы полностью. Если ресурс используется полностью, то в столбце Состояние указывается связанное; при неполном использовании ресурса в этом столбце указывается несвязанное.

Второй тип отчета – Отчет по устойчивости (рис. 1.20). Данный отчет находится на отдельном листе и состоит из двух таблиц.

В столбце Результирующее значение таблицы 1 приводится описанный ранее результат решения задачи. Столбец Нормированная стоимость показывает, что при принудительном включении единицы прод1 в оптимальное решение целевая функция не изменится, прод2 – уменьшится на 10, прод3 – не изменится, прод4 – уменьшится на 20. Столбцы Допустимое увеличение и Допустимое уменьшение показывают, что если прибыль от реализации прод1 будет изменяться в пределах от 60–40 до 60+12, то оптимальное решение задачи не изменится, аналогично для прод2 – от 70–10 до 70+(1Е+30), прод3 – от 120–30 до 120+13,33333333, прод4 – 130–20 до 130+(1Е +30).

В столбце Результирующее значение таблицы 2 приводятся величины использованных ресурсов. Столбец Теневая цена показывает, что при увеличении трудовых ресурсов на единицу оптимальное значение целевой функции увеличится на 20, при увеличении сырья на единицу целевая функция не изменится, при увеличении на единицу финансов оптимальное значение целевой функции возрастет на 10.

Рис. 1.20.

Теневая цена позволяет определить максимальную цену, по которой стоит покупать дополнительные единицы ресурсов. Столбцы Допустимое увеличение и Допустимое уменьшение показывают, что изменение трудовых ресурсов в пределах от 16–3,545454 до 16+6 не приводит к изменению оптимального набора выпускаемых продуктов, аналогично для сырья – от 110–(1Е +30) до 110+26, для финансов – от 100–60 до 100+36.

Третий тип отчета – Отчет по пределам (рис. 1.21). Данный отчет состоит из одной таблицы.

В таблице указаны нижние и верхние пределы, в которых может изменяться выпуск продукции, вошедшей в оптимальное решение.