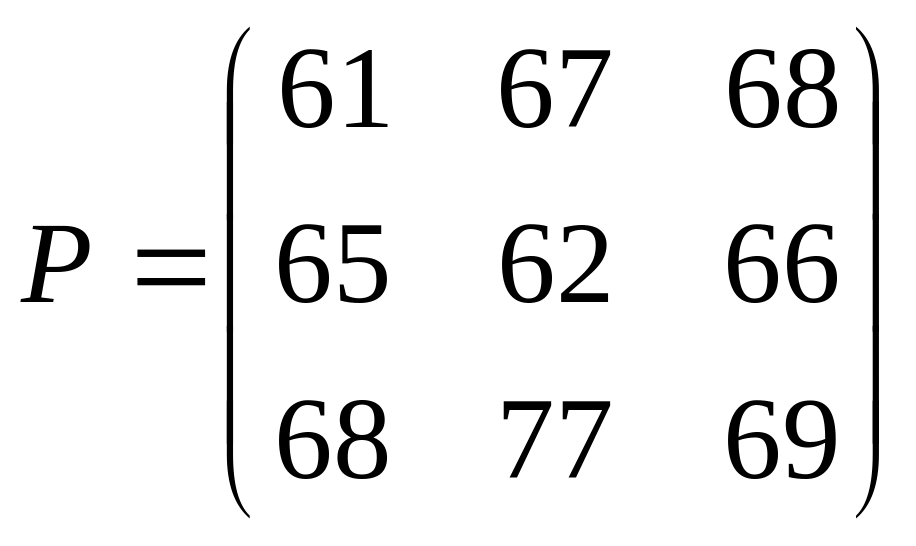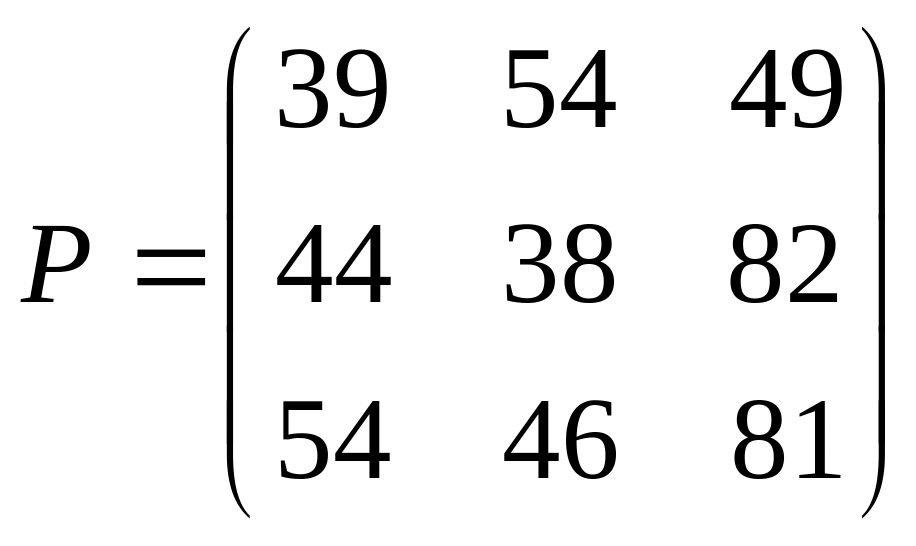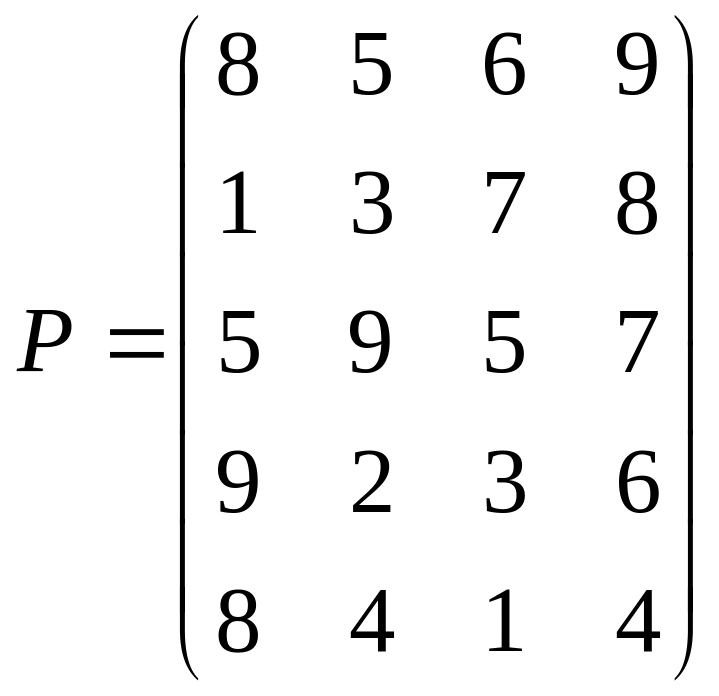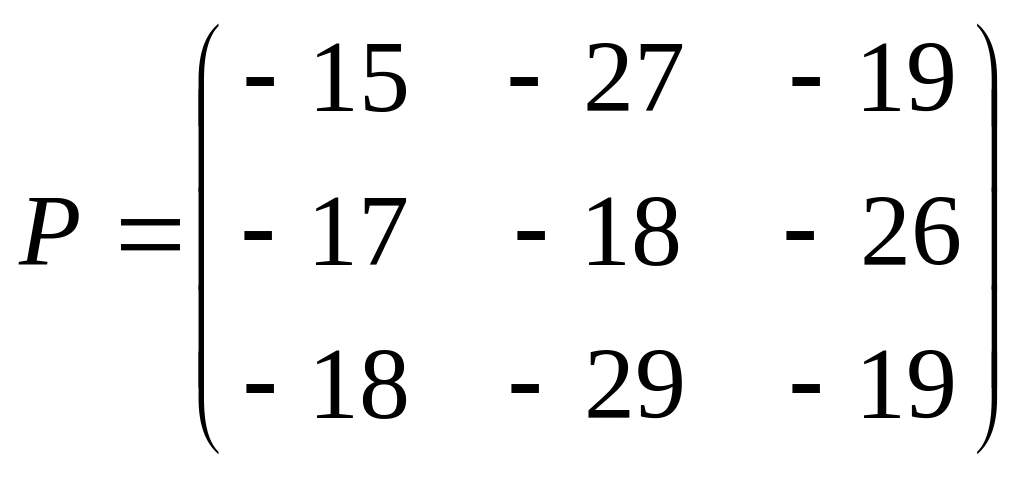- •Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
- •Учебно-методический комплекс
- •1. Рабочая учебная программа дисциплины
- •1.1. Цели и задачи дисциплины
- •1.2. Структура и объем дисциплины Распределение фонда времени по семестрам, неделям, видам занятий
- •1.3. Содержание дисциплины
- •1.4. Требования к уровню освоения дисциплины и формы текущего и промежуточного контроля
- •Примерный перечень вопросов для подготовки к экзамену по дисциплине «Теория принятия решений»
- •1.5. Содержание самостоятельной работы
- •Распределение самостоятельной работы студентов по темам с указанием времени
- •Содержание каждого вида самостоятельной работы и вида контроля
- •2. Учебно-методическое пособие по практическим занятиям Введение
- •2.1. Линейное программирование
- •2.1.1. Постановка задачи
- •2.1.2. Симплексный метод
- •2.1.3. Решение задачи линейного программирования средствами Excel
- •2.1.4. Двойственная задача и ее решение
- •2.2. Целочисленное программирование
- •2.2.1. Метод Гомори
- •2.2.2. Метод ветвей и границ
- •2.2.3. Алгоритм решения задачи целочисленного программирования средствами Excel
- •2.2.4. Транспортная задача
- •2.2.5. Решение транспортной задачи средствами Mathcad
- •2.2.6. Решение транспортной задачи средствами Microsoft Excel
- •2.2.7. Решение задачи о назначении средствами Mathcad
- •2.2.8. Решение задачи о назначении средствами Microsoft Excel
- •2.2.9. Решение задач нелинейного программирования средствами Microsoft Excel
- •2.3. Матричные игры
- •2.3.1. Основные понятия теории игр
- •2.3.2. Решение игр в чистых стратегиях (с седловой точкой)
- •2.3.3. Приведение решения матричной игры к решению задачи линейного программирования
- •2.3.4. Игры с природой
- •2.3.5. Критерии принятия решения
- •1. Критерий Байеса
- •2.4. Практические работы
- •2.4.1. Практическая работа №1
- •1.1. Одноиндексные задачи лп
- •1.2. Ввод исходных данных
- •1.3. Решение задачи
- •1.4. Целочисленное программирование
- •1.5. Двухиндексные задачи лп
- •1.6. Задачи с булевыми переменными
- •1.7. Возможные ошибки при вводе условий задач лп
- •2.4.2. Практическая работа № 2 «Одноиндексные задачи линейного программирования»
- •2.1. Теоретическая часть
- •Целевая функция (цф)
- •При ограничениях
- •19 Верхних и нижних стенок, 12 верхних и нижних стенок,
- •9 Боковых стенок 36 боковых стенок
- •2.4.3. Практическая работа № 3 «Анализ чувствительности одноиндексных задач линейного программирования»
- •3.1. Теоретическая часть
- •3.1.1. Задачи анализа оптимального решения на чувствительность
- •3.1.2. Графический анализ оптимального решения на чувствительность
- •3.1.3. Анализ оптимального решения на чувствительность в Excel
- •3.1.3.1. Отчет по результатам
- •3.1.3.2. Отчет по устойчивости
- •2.4.4. Практическая работа № 4 «Двухиндексные задачи линейного программирования. Стандартная транспортная задача»
- •4.1. Теоретическая часть
- •4.1.1. Стандартная модель транспортной задачи (тз)
- •4.1.2. Пример построения модели тз
- •2.4.5. Практическая работа № 5 «Двухиндексные задачи линейного программирования. Задача о назначениях»
- •5.1. Теоретическая часть
- •5.1.1. Задача о назначениях
- •5.1.2. Постановка задачи о назначениях
- •5.1.3. Рекомендации к решению задачи о назначениях
- •2.4.6. Практическая работа № 6 «Двухиндексные задачи линейного программирования. Организация оптимальной системы снабжения»
- •6.1. Постановка задачи
- •6.2. Рекомендации к решению задачи
- •2.4.7. Лабораторная работа № 7 «Двухиндексные задачи линейного программирования. Оптимальное распределение производственных мощностей»
- •7.1. Теоретическая часть
- •7.2. Постановка задачи распределения производственных мощностей
- •7.3. Построение и решение рз лп
- •2.5. Контрольные задания
- •2.5.1. Линейное программирование
- •2.5.2. Двойственные задачи
- •2.5.3. Целочисленное программирование
- •2.5.4. Транспортная задача
- •2.5.5. Матричные игры*)
- •2.5.6. Приведение решения матричной игры к решению задачи линейного программирования*)
- •2.5.7. Игры с природой
- •2.5.8. Нелинейное программирование
- •2.6. Задания для самостоятельного решения
- •2.6.1. Самостоятельная работа № 1
- •2. Задачи работы:
- •3. Общее описание задания
- •4. Варианты задания
- •5. Требования к оформлению результатов
- •2.6.2. Самостоятельная работа № 2
- •2. Задачи работы:
- •3. Общее описание задания
- •4. Варианты задания
- •5. Требования к оформлению результатов
- •2.6.3. Самостоятельная работа № 3
- •2. Задачи работы:
- •3. Общее описание задания
- •4. Варианты задания
- •5. Требования к оформлению результатов
- •2.6.4. Самостоятельная работа № 4
- •2. Задачи работы:
- •3. Общее описание задания
- •4. Варианты задания
- •5. Требования к оформлению результатов
- •2.6.5. Самостоятельная работа № 5
- •2. Задачи работы:
- •3. Общее описание задания
- •4. Варианты задания
- •2.6.6. Самостоятельная работа № 6
- •2. Задачи работы:
- •3. Общее описание задания
- •4. Варианты задания
- •5. Требования к оформлению результатов
- •2.7. Задания для тестирования Вариант № 1
- •3. Транспортная задача
- •Вариант № 2
- •3. Транспортная задача
- •Вариант № 3
- •3. Транспортная задача
- •Вариант № 4
- •3. Транспортная задача
- •Вариант № 5
- •3. Транспортная задача
- •Вариант № 6
- •3. Транспортная задача
- •Вариант № 7
- •3. Транспортная задача
- •Вариант № 8
- •3. Транспортная задача
- •Вариант № 9
- •3. Транспортная задача
- •Вариант № 10
- •3. Транспортная задача
- •Вариант № 11
- •3. Транспортная задача
- •Вариант № 12
- •3. Транспортная задача
- •Вариант № 13
- •3. Транспортная задача
- •Вариант № 14
- •3. Транспортная задача
- •Вариант № 15
- •3. Транспортная задача
- •Вариант № 16
- •3. Транспортная задача
- •Вариант № 17
- •3. Транспортная задача
- •Вариант № 18
- •3. Транспортная задача
- •Вариант № 19
- •3. Транспортная задача
- •Вариант № 20
- •3. Транспортная задача
- •Вариант № 21
- •3. Транспортная задача
- •Вариант № 22
- •3. Транспортная задача
- •Вариант № 23
- •3. Транспортная задача
- •Вариант № 24
- •3. Транспортная задача
- •Вариант № 25
- •3. Транспортная задача
- •Вариант № 26
- •3. Транспортная задача
- •Вариант № 27
- •3. Транспортная задача
- •Вариант № 28
- •3. Транспортная задача
- •3. Учебно-методическое обеспечение дисциплины
- •3.1. Перечень основной и дополнительной литературы
- •3.1.1. Основная литература:
- •3.1.2. Дополнительная литература:
- •3.2. Методические рекомендации преподавателю
- •3.3. Методические указания студентам по изучению дисциплины
- •3.4. Учебно-методическая карта дисциплины
- •3.5. Материально-техническое обеспечение дисциплины
- •3.6. Программное обеспечение использования современных информационно-коммуникативных технологий
- •3.7. Технологическая карта дисциплины Поволжский государственный университет сервиса
- •Решение задач линейного программирования симплекс-методом
- •Решение задач систем массового обслуживания
- •П.3.2. Решение задачи смо традиционными методами
- •П.3. Решение задачи смо с использованием системы Mathcad
2.5.6. Приведение решения матричной игры к решению задачи линейного программирования*)
Найдите решение игр, определяемых следующими матрицами:
1. |
|
2. |
|
3. |
|
||
|
|
|
|
|
|
||
4. |
|
5. |
|
6. |
|
||
|
|
|
|
|
|
||
7. |
|
8. |
|
9. |
|
||
|
|
|
|
|
|
||
10. |
|
11. |
|
12. |
|
||
|
|
|
|
|
|
||
13. |
|
14. |
|
15. |
|
||
|
|
|
|
|
|
||
16. |
|
17. |
|
18. |
|
||
19. |
|
20. |
|
||||
|
|
|
|
||||
21. |
|
22. |
|
||||
|
|
|
|
||||
23. |
|
24. |
|
||||
|
|
|
|
||||
25. |
|
26. |
|
||||
|
|
|
|
||||
27. |
|
28. |
|
||||
|
|
|
|
||||
29. |
|
30. |
|
||||
|
|
|
|
||||
31. |
|
32. |
|
||||
|
|
|
|
||||
33 |
|
34. |
|
||||
|
|
|
|
||||
35. |
|
36. |
|
||||
|
|
|
|
||||
37. |
|
38. |
|
||||
|
|
|
|
||||
39. |
|
40. |
|
||||
|
|
|
|
||||
41. |
|
42. |
|
||||
|
|
|
|
||||
43. |
|
44. |
|
||||
45. Составить матрицу игры двух игроков. Игроки называют по одной цифре из трёх: 1, 2 или 3. Если разность получается чётная, одно очко выигрывает первый игрок, если нечётная, то одно очко выигрывает второй игрок. Проигрыш игрока равен выигрышу его противника, но в матрицу игры записывается со знаком «−».
46. Два игрока бросают по очереди игральную кость (кубик). Бросив в свою очередь кубик, игрок продвигается по трассе игры на то число клеток, какое выпало на кубике. Это передвижение называется одним ходом игрока. Выигрывает тот, кто уйдёт дальше от начала дорожки. Другими словами, тот, у кого сумма чисел, выпавших за все сделанные в процессе игры ходы, на кубике будет наибольшей.
Составьте матрицу игры для возможных стратегий игроков в случае, если игра заканчивается через: а) один ход; б) два хода; в) три хода.
47. У двух игроков имеются по две карточки: на одной изображён заяц, а на другой − белка. Игроки показывают одновременно и независимо друг от друга одну из двух своих карточек. Затем убирают их и ещё раз показывают одну из своих карточек. Если за два хода игроки покажут больше двух зайцев, то выигрывает первый игрок, и его выигрыш равен числу показанных зайцев. И наоборот, если показано больше двух белок, то выигрывает второй игрок, и его выигрыш равен числу показанных белок. Найдите цену этой игры.
48. Два шахматиста сыграли друг с другом 12 партий. При этом их результаты получились такими, как задано в матрице платежей

Каких стратегий им придерживаться в следующем турнире, чтобы игра для них была оптимальной?
49. Играют два игрока, составляя слова из букв слова «машина». Выигрывает тот, кто составит слова, сумма букв в которых будет больше. При этом совпадающие у противников слова не засчитываются. Сумма букв всех несовпадающих слов выигрывающего игрока засчитывается ему как выигрыш. Составьте матрицу игры.
50. Две фирмы продают на рынке четыре вида одинаковых товаров в течение трёх месяцев по отличающимся ценам. Зарегистрированная разница между ценами фирм на товары одинакового наименования для каждого из трёх месяцев указана в матрице.
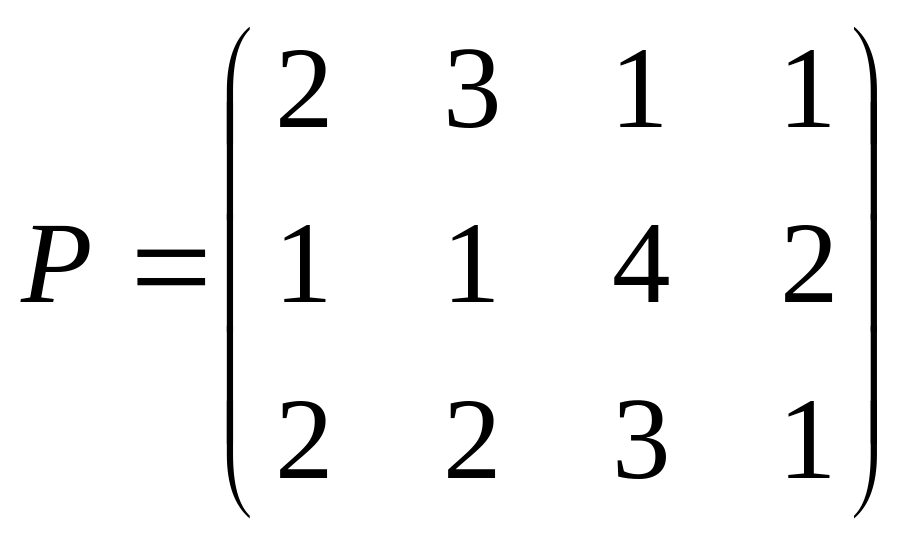
Поскольку цены на все товары у первой фирмы все три прошедших месяца были меньше, то потребитель охотнее покупал её товары.
Найдите оптимальное решение этой игры.