3. Парная регрессия и корреляция

15. Функциональные и стохастические типы связей. Ковариация, корреляция

Между двумя переменными может быть:

1. Функциональная связь — каждому значению одной переменной соответствует вполне определенное значение другой.

2. Стохастическая (статистическая, корреляционная) связь — одному и тому же значению одной переменной соответствует некоторое распределение значений другой.

По направлению связь может быть:

1. прямой — если при увеличении одной переменной другая в среднем возрастает.

2. обратной — если при увеличении одной переменной другая в среднем убывает.

Мерой взаимосвязи между переменными X и Y может служить выборочная ковариация:

,

где n — число наблюдений.

Если — между переменными прямая связь, если — обратная. Ковариация зависит от единиц измерения переменных, что является ее существенным недостатком.

Пример 1. По десяти однородным предприятиям имеется информация, характеризующая зависимость годовой выручки от продаж (Y, млн. руб.) от среднегодовой стоимости активов (X, млн. руб.):

№ предприятия	x	y
1	22	26
2	48	52
3	31	43
4	36	38
5	43	54
6	52	53
7	28	35
8	26	37
9	42	47
10	59	58
Среднее	38,7	44,3
Стандартное отклонение	12,1	10,2

С помощью функции Excel «КОВАР» было получено значение ковариации между X и Y: . Так как , то это свидетельствует о прямой связи между выручкой от продаж и стоимостью активов.

16. Анализ линейной статистической связи экономичес­ких данных, корреляция; вычисление коэффициентов корреляции, проверка значимости

Основная задача корреляционного анализа заключается в выявлении взаимосвязи (корреляции) между переменными, для чего вместо ковариации более эффективно использовать выборочный парный коэффициент корреляции:

,

где S_x, S_y — средние квадратические (стандартные) отклонения переменных X и Y:

; .

Свойства коэффициента корреляции:

1. r_y,x непосредственно не устанавливает причинно-следственных связей.

2. r_y,x характеризует направление и тесноту (силу) линейной связи между переменными.

3. r_y,x является безразмерной величиной и может принимать значения от –1 до +1.

4. При абсолютной независимости переменных .

5. Если — между переменными прямая связь, если — обратная.

6. Чем ближе r_y,x по модулю к единице, тем теснее связь между переменными.

7. Если переменные связаны линейной функциональной связью, то .

8. Связь между переменными принято считать тесной, если .

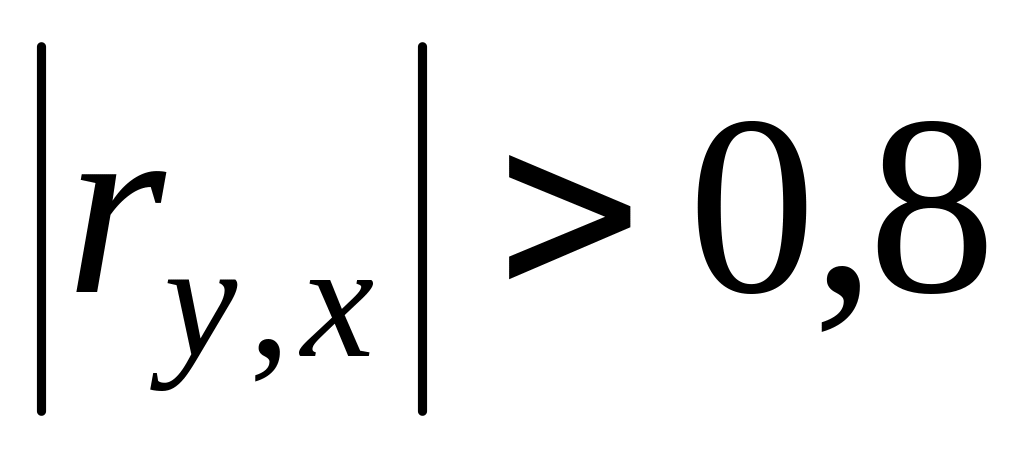9. Факт наличия статистически значимой линейной связи может считаться установленным, если

,

где r_кр — критическое (табличное) значение при принятом уровнем значимости  и числе степеней свободы .

В противном случае считается, что связь слабая либо отсутствует вообще.

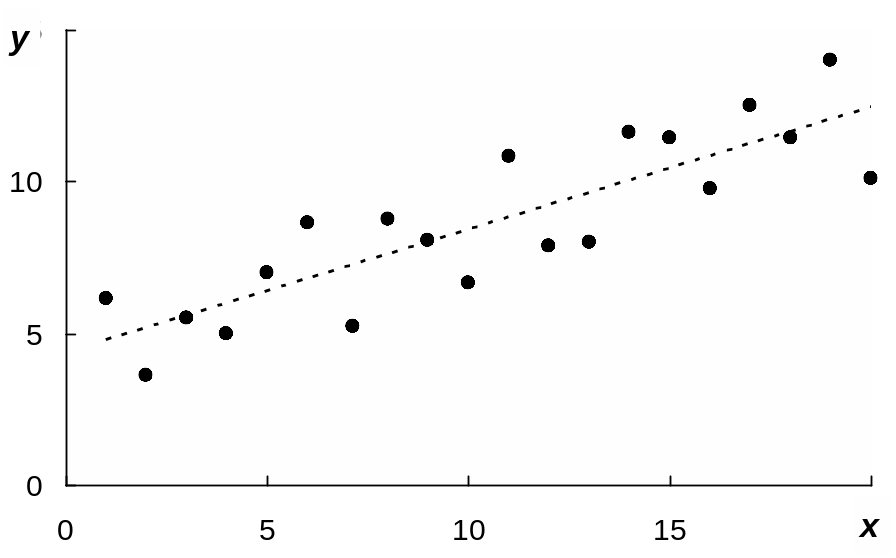
а) прямая и обратная функциональные связи	б) прямая ( ) тесная ( ) связь
в) обратная ( ) умеренная ( ) связь	г) прямая ( ) слабая ( ) связь
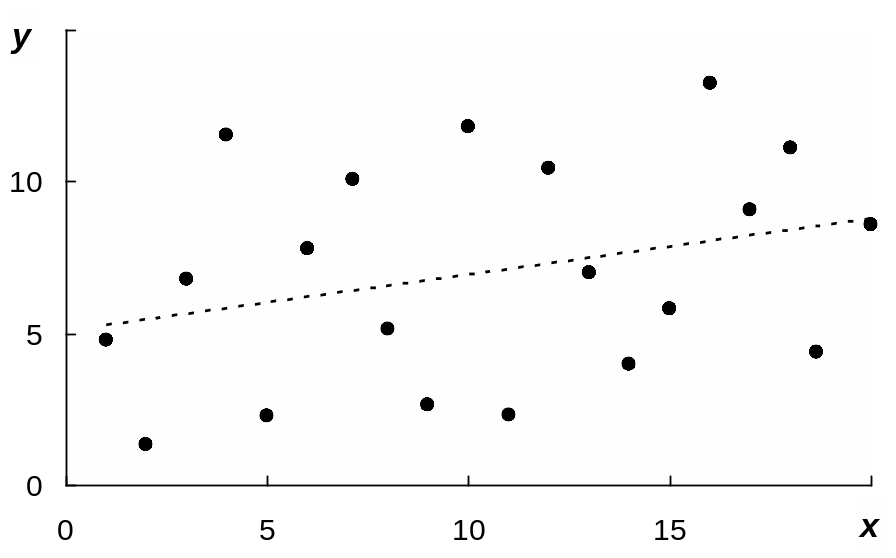
д) связь отсутствует ( )	е) ярко выраженная нелинейная связь ( )

Продолжение примера 1. С помощью функции Excel «КОРРЕЛ» (или «ПИРСОН») было получено значение коэффициента корреляции: , который показывает, что между переменными имеется прямая ( ) тесная ( ) линейная связь.

Критическое значение при =0,05 и составляет r_кр=0,632. Так как , то связь между выручкой от продаж и среднегодовой стоимостью активов признается статистически значимой.