34. Свойства оценок метода наименьших квадратов (мнк)

Коэффициенты уравнения регрессии b₀, b₁, b₂, …, b_p являются случайными величинами. Если выполняются предпосылки 1 — 4 МНК, то они обладают следующими свойствами:

1. Несмещенности. Математическое ожидание коэффициента равно соответствующему истинному параметру регрессии:

.

2. Эффективности. Они характеризуются наименьшей дисперсией:

.

3. Состоятельности. При увеличении числа наблюдений увеличивается точность оценки:

.

Невыполнение предпосылки 5 не позволяет корректно оценить точность и проверить статистическую значимость уравнения регрессии и его параметров.

35. Проверка выполнения предпосылок метода наименьших квадратов (мнк)

Проверка предпосылки 1 может проводиться путем визуального анализа графиков остатков от значений факторов либо от предсказанных уравнением регрессии значений результата Y. Остатки считают случайными, если на графике они расположены в виде горизонтальной полосы:

Выполнение предпосылки 5 может проверяться с помощью R/S‑критерия

,

где e_max, e_min — соответственно наибольший и наименьший остатки с учетом знака; S_e — среднее квадратическое (стандартное) отклонение ряда остатков:

.

Остатки признаются нормально распределенными, если

.

где (R/S)₁ и (R/S)₂ — критические границы R/S-критерия для принятого уровня значимости  и числа наблюдений n.

Продолжение примера 3. Значения остатков регрессии были получены в EXCEL при проведении регрессионного анализа. Наибольший и наименьший остатки составляют: e_max=3,88; e_min=–4,29. Среднее квадратическое отклонение остатков равно

,

а R/S‑критерий

попадает в критические границы (R/S)₁=2,80 и (R/S)₂=3,91 (=0,05; n=12). Остатки признаются нормально распределенными.

36. Понятие и причины гетероскедастичности. Последствия гетероскедастичности. Обнаружение гетероскедастичности

Гетероскедастичность остатков проявляется в том, что их дисперсия (разброс) зависит от значений факторов:

и:

Гетероскедастичность приводит к тому, что может быть ошибочно принято решение о статистической значимости коэффициентов регрессии, тогда как на самом деле это не так.

Выполнение предпосылки 3 может проверяться методом Глейзера, для чего рассчитывается коэффициент корреляции между абсолютными величинами остатков и расчетными значениями (i=1, 2, …, n). Гетероскедастичность остатков отсутствует, если

,

где r_кр — критическое значение при принятом  и .

Продолжение примера 3. Коэффициент корреляции — , критическое значение — r_кр=0,576 (=0,05; ). Так как , гетероскедастичность остатков не выявлена.

37. Понятие и причины автокорреляции остатков. Последствия автокорреляции остатков. Обнаружение автокорреляции остатков

Автокорреляции остатков наблюдается тогда, когда значения предыдущих остатков завышают (положительная) или занижают (отрицательная) значения последующих.

Положительная автокорреляция на графике остатков проявляется в чередовании зон положительных и отрицательных остатков:

Отрицательная автокорреляция на графике выражается в том, что остатки «слишком часто» меняют знак:

Основными причинами автокорреляции являются:

• неправильный выбор формы регрессионной зависимости;

• неучет в модели одного или нескольких важных факторов;

• цикличность значений экономических переменных при построении модели по временным данным.

Автокорреляция может привести к ошибочному выводу о несущественном влиянии исследуемого фактора на результат Y, в то время как на самом деле влияние фактора на Y значимо.

Для обнаружения автокорреляции остатков используется d-статистика Дарбина–Уотсона:

.

Значение d-статистики сравнивается с критическими значениями d₁ и d₂. При этом могут возникнуть следующие ситуации:

• если , то остатки признаются некоррелированными;

• если , то имеется положительная автокорреляция;

• если , то существует отрицательная автокорреляция;

• если или , то это указывает на неопределенность ситуации.

d‑статистика рассчитывается либо по временному ряду остатков, либо по упорядоченному в зависимости от последовательно возрастающих или убывающих расчетных значений Y.

При неопределенности ситуации рассчитывается коэффициент автокорреляции остатков первого порядка

.

Автокорреляция отсутствует, если коэффициент не превышает по модулю критическое значение. В противном случае делают вывод о наличие автокорреляции: положительной при или отрицательной при .

Продолжение примера 3. d‑статистика имеет значение d=3,44. Критические значения составляют d₁=0,66 и d₂=1,86 (=0,05; p=3; n=12). d‑статистика попадает в интервал , что свидетельствует об отрицательной автокорреляции остатков.

Коэффициент автокорреляции остатков первого порядка r₍₁₎=–0,721 превышает по модулю критическое значение r_кр=0,576 (=0,05; n=12), что еще раз свидетельствует об отрицательной автокорреляции остатков.
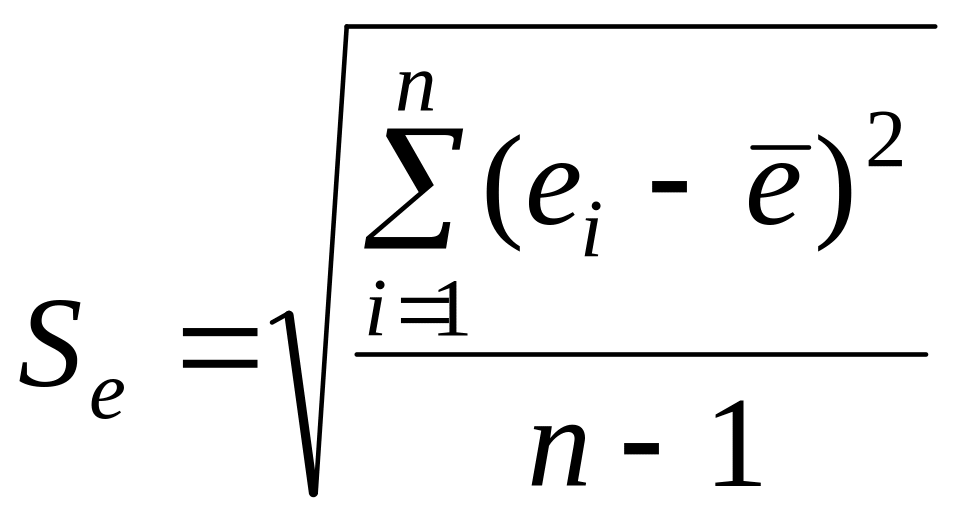