20 Вопрос Координатная форма векторов.

Е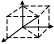 сли вектор а задан в виде а=Xi+Yj+Zk то говорят что он задан в координатной форме. Вектор ОМ и а - диагональ параллелепипеда и соотв. |а| =sqr(X²+Y²+Z²) (XYZ—коорд. вектора a или проекции a на оси коорд.)

X= |a| *cosL =>cosL = x/sqr (x²+y²+z²)

Y= |a| *cosL =>cos B = y/sqr (x²+y²+z²)

Z= |a| *cosL =>cos = z/sqr (x²+y²+z²)

направляющие cos вектора a

Они связаны следующим соотношением: cos²L+cos²B+cos² =1

Вопрос 21 Свойство векторов заданных в заданной коорд. Форме.

Для этих векторов существ. След св-ва:

1) два вектора равны если равны их координаты а=X₁i+Y₁j+Z₁k; b=X₂i+Y₂j+Z₂k; X₁=X₂; Y₁=Y₂; Z₁=Z₂

2)При сложении векторов в зад. коорд. форме их коорд. складываются а=X₁i+Y₁j+Z₁k; b=X₂i+Y₂j+Z₂k; (a+b)=(X₁+X₂)i+(Y₁+Y₂)j+(Z₁+Z₂)k

3)При вычитании векторов их коорд. Вычитаются a=X₁i+Y₁j+Z₁k; b=X₂i+Y₂j+Z₂k

(a-b)= (X₁-X₂)i+(Y₁-Y₂)j+(Z₁-Z₂)k

4)При умножении вектора на скаляр все координаты этого вектора умножаются на данный скаляр a=X1i+Y1j+Z1k (λ—скаляр) λА= λXi+ λYj+ λZk

5)Условие колинеарности 2-х векторов заданных в коорд. форме a=X₁i+Y₁j+Z₁k; b=X₂i+Y₂j+Z₂k Если a коллинеарен b то всегда можно найти такой постоянный множитель λ что λb=a. λb= λX₂i+ λY₂j+ λZ₂k a и λb равны, а значит их координаты т.е. X₁= λX₂; Y₁= λY₂; Z₁= λZ₂ λ=X₁/X₂; λ=Y₁/Y₂; λ=Z₁/Z₂ --- X₁/X₂=Y₁/Y₂=Z₁/Z₂(*) Если коорд. вектора a и b удовлетворяют соотношение (*) то λb=a т.е. a и b коллинеарны. Соотношение (*) это условие колинеарности векторов т.о. векторы коллинеарны тогда и только тогда когда их координаты пропорциональны.

22 Вопрос Скалярное произведение векторов.

Скалярное произведение 2-х векторов это число равное произведению их модулей (длин) умноженному на cos угла между векторами т.е. (a,b)= |a|*|b|cosφ. Скалярное произведение a и b будет равно 0 в 2-х случаях:

1. Если хотя бы 1 из векторов a или b является нулевым вектором.

2. Если векторы перпендикулярны

(a,b)=0

Свойства скалярного произведения:

1) скал произв подчиняется переместит. закону (а,b)=(b,a)

2) подчин сочетательному закоу относительно скалярного множителя (λa,b)= λ(a,b) (для любых λ,a,b)

3) подчин распределительному закону a(b+c)=ab+ac (для любых a,b,c)

4) Скалярный квадрат вектора равен квадрату его модуля (a,a)= |a|*|a|cos0=|a|² т.е. (a²) = |a|²

5) Скалярное произведение векторов, заданных в коорд. форме a=X₁i+Y₁j+Z₁k; b=X₂i+Y₂j+Z₂k Правые части этих векторов можно перемножить по правилу умножения многочлена на множитель т.к. скал произв подчин распределит закону (a,b)=X₁X₂+Y₁Y₂+Z₁Z₂ т.о. скалярное произвед 2-х векторов заданных в коорд форме равно сумме произведений одноименных координат этих векторов

Вопрос 23. Векторное произведение неколлинеарных векторов, его свойства.

Э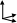 то вектор С длинна которого равна площади параллелограмма, построенного на векторах a и b, который перпендикулярен плоскости этого параллелограмма и направлен так, что если смотреть с его конца, то кратчайший поворот от a к b происходит против часовой стрелки. Если a и b коллинеарны, то их векторным произведением называется 0 вектор.

Е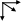 сли векторно умножить b на a, то получим вектор [b,a] равен по модулю вектору [a,b], но направленный в противоположную сторону т.е. [a,b]=-[b,a].

Если вектора a и b коллинеарны, то их векторное произведение равно 0 .

(a,b)=|a|*|b|*cos

Свойства

1. Для любых векторов a и b, векторное произведение не подчиняется переместительному закону.

2. Векторное произведение подчиняется сочетательному закону относительно скалярного множителя.

для любых λ,a,b

3. Векторное произведение подчиняется распределительному закону