Вопрос 1. Система координат. Координаты на прямой.
П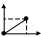
усть
дана некоторая прямая, установим на ней
положение направления, прямая стала
осью . Выберем
на ней произв. точку (о), зададим единичный
или масштабный отрезок – (о) начало
отсчета. Если на прямой выбранно
направление, начальная точка (о) и начало
отсчета, то говарят, что на этой прямой
введена декартова система координат.
При этом прямая называется координатной
осью, (о) – начало координат. Введение
на прямой д.с.к. позволяет определить
положение точек этой прямой с помощью
действительных чисел. Координатой любой
точки М прямой в выдранной системе
координат называется число х равное
величине равновестного отрезка ОМ
(х=ОМ).
Т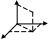
.О.
х – это координата точки М, число равное
по абсолютной величине расстоянию от
начала координат до точки М и это число
имеет знак (+)при совпадении с осью и (-)
если направление не совпадает с осью.
При помощи д.с.к. на прямой можно установить
взаимноодназначное соответствие между
множеством всех точек прямой и множеством
всех действительных чисел. Любой точке
прямой соответствует определенной
действ. число, а любому действ. числу
опр. точка на прямой.
Вопрос 2. Декартова система коорд. На плоскости.
Будем говорить, что на плоскости заданна д.п.с.к. если заданна пара взаимно перпендикулярных осей, при этом установленно какая первая какая вторая, задан единичный или масштабный отрезок. Точку (о) – точку пересечения осей будем считать началом координат. Первая ось- ось абсцис (ОХ), вторая – ось ординат (ОУ).
М
– произвольная точка плоскости, опустим
перпендикуляр на оси ОХ и ОУ. Абсциссой
точки М назыв. величина отрезка ОК оси
ОХ, ординатой – отр. OL
оси ОУ. Пару чисел Х и У, где х = ОК, у = OL
назыв. координатами точки М в выбранной
системе координат. М (х,у). Абсцисса Х
точки М = 0 тогда и только тогда, когда
точка М лежит на оси ОУ, ордината У – на
оси ОХ. Т.О. каждой точке М соотв. пара
действ. чисел х,у ,координат этой точки
и наоборот.
М
1(х1,у1)
М2(х2,у2)
Эта формула позволяет зная координаты точек М1 и М2 определить расстояние между этими точками.
Вопрос 3. Полярная система координат на плоскости.
В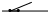
озьмем
на плоскости точку (О) и проходящую ось
ОР. Точку (О) будем называть полюсом,
а луч исходящий
из полюса будем называть полярной осью.
Задание полюса О полярной оси ОР и
единичного отрезка ОЕ на этом луче
определяет на плоскости полярную систему
координат. Полярным радиусом ρ точки М
плоскости называется ее расстояние от
полюса О т.е. длинна отрезка ОМ. φ –
полярный угол, это угол наклона
направленного отрезка ОМ полярной оси
ОР. φ определяется с учетом знака и с
точностью до слагаемого 2πк, к- любое
целое число. 0≤φ≤2π Числа ρ и φ называются
полярными коор-ми точки М
Вопрос 4. Связь между прямоугольными декартовыми и полярными координатами.
Наряду с введенной полярной системой координат рассмотрим прямоугольную декартову систему такую, что полюс совпадает с началом, а полярная ось – с положительной полуосью Ох. Если М произвольная точка плоскости, (х,у) – ее декартовы, а (ρ,φ) – полярные координаты, то очевидно, что х= ρcos φ, y= ρcosφ
Вышеуказанные
формулы выражают прямоугольные декартовы
координаты точки плоскости через ее
полярные координаты. Полярные координаты
точки выражаются через ее декартовы
координаты формулами: ρ=
,
cosφ=
,
sinφ=