
Лекція № 10
тема : РОЗТЯГ Та СТИСК СТЕРЖНЯ (БРУСА)
План
1. Умови рівноваги. Метод перерізів
2. Напруження
3. Розтяг – стиск
4. Деформації при розтягу – стиску
5. Основні положення для вибору коефіцієнта запасу міцності та допустимих напружень
ВИКЛАД ТЕМИ
1. Умови рівноваги. Метод перерізів
У зв΄язку з тим, що опір матеріалів розглядає деформації тіл, у більшості випадків нехтуючи їх рухом, одними з основних математичних залежностей, що використовуються, є рівняння рівноваги.
В загальному випадку просторової задачі (рис.1.5), вибравши ортогональну декартову систему координат, їх можна сформулювати так:
суми проекцій всіх сил, що діють на тіло, на відповідні осі дорівнюють нулю;
суми моментів усіх сил, що діють на тіло, відносно будь-якої координатної осі дорівнюють нулю.
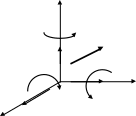 Z
Z
Mz
Fz F
My Y
Mx Fy
Х Fx
Рис.1.5. Силові фактори при загальному випадку просторового
навантаження
Або
символічно:
![]() (1.1')
(1.1')
(1.1)
![]() (1.1'')
(1.1'')
Зрозуміло, що для плоскої задачі цих рівнянь вже буде тільки три (суми проекцій сил на кожну з осей рівні 0 та сума моментів всіх сил відносно будь якої довільної точки цієї площини теж дорівнюють 0).
![]() (1.2)
(1.2)
У випадку лінійного навантаження (уздовж однієї осі) рівняння рівноваги буде тільки одне – алгебраїчна сума всіх сил повинна дорівнювати 0.
![]() (1.3)
(1.3)
При розгляді стержневих систем постає питання про знаходження внутрішніх сил, що діють у будь-якому довільному перерізі. Для цього може бути використано



метод перерізів, суть якого полягає у тому, що внутрішній силовий
фактор (сила, момент) у перерізі знаходиться як алгебраїчна сума всіх
сил,взятих з одного боку від цього перерізу
Суть методу зображено на рис.1.6,а,б,в.
Чому саме з одного боку? Тому, що за законами рівноваги сума сил з другого боку повинна дорівнювати тій же величині та бути спрямованою в протилежний бік (рис 1.6,в), виходячи з (1.3).
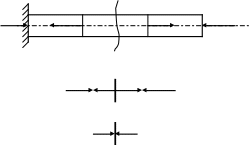 1
kH m 2 kH
1
kH m 2 kH
R=2kH 3 kH
n
a)
2kH 1kH 2kH 3kH
б)
1 kH 1 kH
в)
Рис. 1.6. Ілюстрація методу перерізів
Слід зауважити, що, по-перше, реакції опор – це також зовнішні сили і ними не можна нехтувати, по-друге, якщо зображений на рисунку вектор сили направлений в один бік, а величина сили за обчисленнями дорівнює від’ємному числу, то насправді сила спрямована в інший бік. Користуючись цим методом неважко побудувати епюру навантажень у наведеному стержні (рис 1.7).
Таким чином від системи зовнішніх сил можна перейти до внутрішніх силових факторів, тобто тих сил і моментів, що діють безпосередньо в перерізі, який нас цікавить.
