3.2 Статистический анализ результатов моделирования
3.2.1 Оценивание вероятностных распределений и их числовых характеристик
Важнейшим этапом в исследование сложных систем является этап статистического анализа результатов экспериментов, к которым относятся выборки значений: входных воздействий; воздействий внешней среды; фазовой и выходной траекторий; показателей эффективности системы. Имитационная модель, описывая динамическое поведение исследуемой стохастической системы во времени, позволяет получить результаты, подобные тем, которые регистрируются в ходе натурных экспериментов с реальной системой. Поэтому для статистического анализа результатов имитационных и натурных экспериментов применимы одни и те же методы. Отличие состоит в том, что имитационное моделирование позволяет получать именно те данные о системе и в том объеме, которые необходимы для решения задач исследования.
В общем случае результаты моделирования образуют некоторый набор выборок, каждая из которых представляет собой ряд случайных величин (данных). Основными задачами статистического анализа таких данных являются:
определение эмпирического закона распределения случайных величин;
проверка однородности распределений;
сравнение средних значений и дисперсий переменных полученных в результате моделирования.
Пусть
– случайная величина (СВ) с функцией
распределения
,
являющаяся математической моделью
единичного наблюдения одной из компонент
или одного из показателей, используемых
в ходе имитационного моделирования.
На
практике наибольшее распространение
имеют два класса функций распределения
:
1) непрерывные
и 2) дискретные.
В первом случае существует плотность
распределения вероятностей СВ
:
.
(3.8)
Во
втором случае СВ
принимает значения из дискретного
множества
,
и имеет дискретное распределение
вероятностей
, 
.
(3.9)
Вероятностная
модель наблюдения
полностью описывается функциональными
характеристиками:
функцией распределения
,
плотностью распределения (3.8) или
дискретным распределением вероятностей
(3.9). Когда получить полное вероятностное
описание не представляется возможным,
то на практике используются числовые
характеристики. Любая числовая
характеристика
является некоторым функционалом от
:
.
Множество числовых характеристик
состоит из двух подмножеств.
Числовые характеристики положения (сдвига):
математическое ожидание (среднее)
;медиана
;
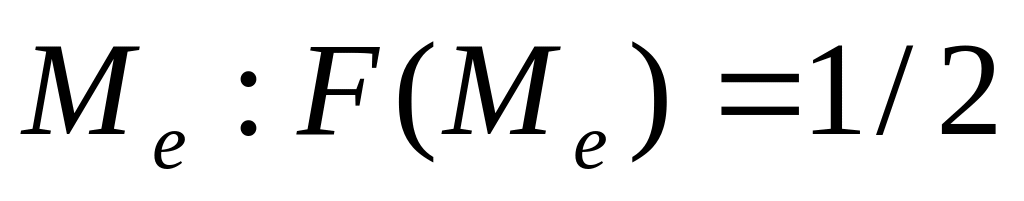мода
;наибольшее
и
наименьшее
значения,
,
.
Числовые характеристики рассеяния (масштаба):
дисперсия
;среднеквадратичное (стандартное) отклонение
;коэффициент вариации (если
)
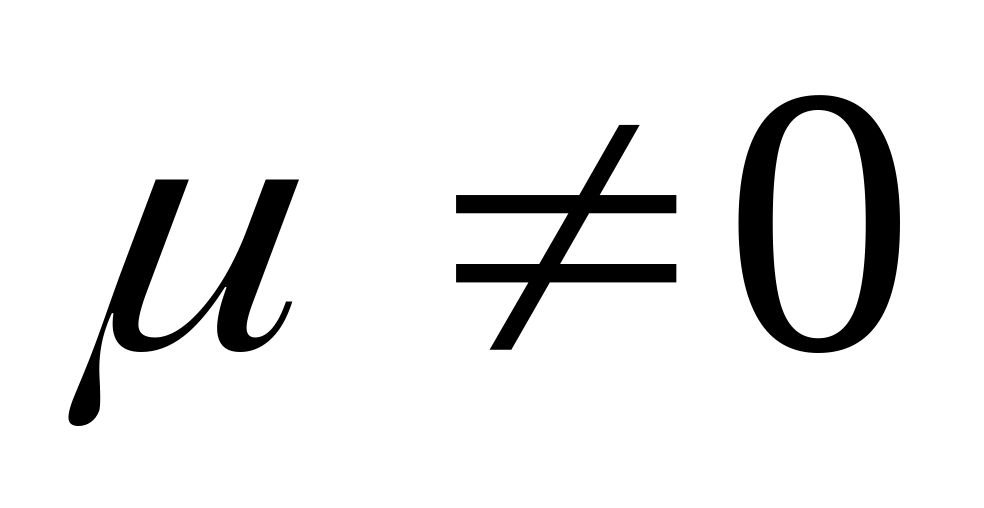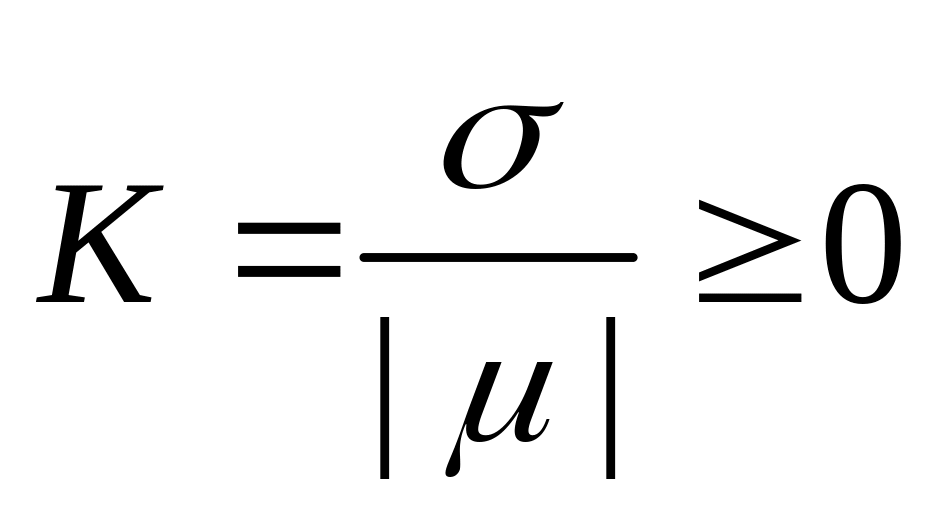;размах
;коэффициент асимметрии
;коэффициент эксцесса (островершинности)
.
Если
имеет гауссовский закон распределения
вероятностей
,
то
,
,
,
,
,
,
,
.
В
процессе моделирования функциональные
и числовые характеристики вероятностного
распределения часто неизвестны и
возникает задача их статистического
оценивания по случайной выборке
объема
из распределения
,
полученной в результате
«независимых прогонов» имитационной
модели. Сначала рассмотрим задачу
оценивания
по
.
Эмпирическая
функция распределения
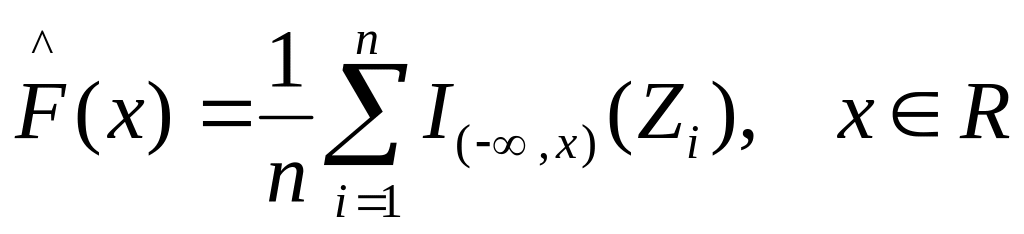(3.10)
является
состоятельной, несмещенной оценкой с
наименьшей вариацией
.
В
случае дискретной вероятностной модели
(3.9) относительная частота
является
несмещенной, состоятельной эффективной
и асимптотически нормально распределенной
оценкой элементарной вероятности
;
при этом вариация
.
В
случае непрерывной вероятностной модели
(3.8) для оценивания плотности
применяется гистограмма. Для её построения
разобьем промежуток
концентрации плотности
на
ячеек точками деления
:
.
Обозначим 
(3.11)
число
выборочных значений из
,
попавших в
–ю
ячейку гистограммы. Гистограммой
является статистика
.
Эта оценка является смещенной и несостоятельной в общем случае.
Для оценивания числовых характеристик по выборке широко используется подстановочный принцип:
,
где
–
выборочная функция распределения
(3.10).
Статистические оценки числовых характеристик положения имеют вид:
;
(3.12)
.
Выборочное
среднее
является состоятельной несмещенной
оценкой с вариацией
.
Статистические точечные оценки числовых
характеристик рассеяния принимают
вид:
(3.13)
