Алгоритм и пример решения задачи № 6

1. Так как фигура симметрична, то очевидно Х_с = 0. Выбираем начальную ось Х₀ (по основанию фигуры).

2. Разбиваем фигуру на простые части. Если фигура с отверстием, то необ­ходимо дополнить (условно) ее до сплошной, а затем при решении пло­щадь отверстия вычесть.

3. Определяем площади и координаты центра тяжести каждой части в от­дельности.

Находим Y_C по формуле .

Первый способ решения:

1. .

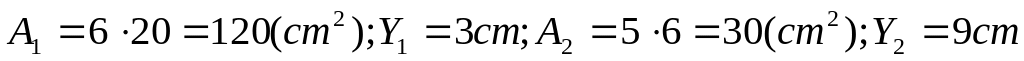1. Определяем статический момент площади: S_Xo 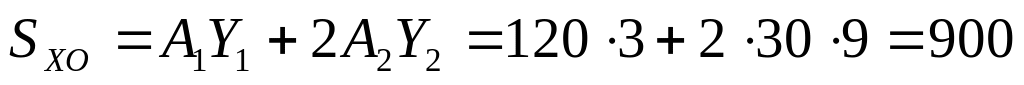(см³).

3. ;или

Второй способ решения (дополняя фигуру до сплошной):

Ответ: Сравнивая результаты двух способов решения, приходим к выводу, что задача решена верно. Y_c = 5 см.

Алгоритм решения задачи № 7

1. Разбить брус на отдельные участки. У каждого участка границами будут яв­ляться сечения, в которых приложены силы, или изменения формы сече­ния бруса.

2. Для определения значений продольных сил воспользоваться методом сечений. Провести сечение 1-1 и мысленно отбросить верхнюю часть бруса. Затем приложить к этому сечению продольную силу N₁ равную сумме внутренних сил в сечении и заменяющую действие отброшенной части на оставшуюся нижнюю часть бруса.

Учитывая состояние равновесия оставшейся нижней части участка l₁ составить уравнение равновесия:

, откуда N_l = F_l.

3. Отбросить верхнюю часть бруса от сечения 2—2, составить уравнение равновесия для оставшейся части бруса и вычислить величину продольной силы на участке 1₂:

, N₂ = F₁

4. Действуя аналогично в отношении сечения 3—3, получить величину продольной силы на участке 1₃:

; N₃ = F₁ –F₂

Из рассмотренного следует, что продольная сила в любом сечении бруса равна алгебраической сумме (с учетом знаков) внешних сил, распо­ложенных (отсекаемых) по одну сторону от сечения. Если сила действу­ет на растяжение, надо брать знак (+), если на сжатие — знак (—).

Поэтому эпюру продольных сил необходимо строить методом прохо­да, идя от свободного конца бруса (см. пример).

5. Определить величину нормальных напряжений в сечении каждого из

участков бруса по формуле .

На участке , на и на .

6. Для построения эпюр продольных сил и нормальных напряжений про­ вести оси, параллельные оси бруса, и отложить известные значения N и σ в масштабе. Положительные значения — вправо, отрицательные — влево.

7. Определить абсолютное удлинение (укорочение) длины бруса по форму­ле Гука

для каждого участка. Полное удлинение или укорочение получается путем сложения (с учетом знаков): .

Пример решения задачи № 7

Дано: F₁ = 50 кН; F₂= 20 кН; l₁ = 0,8 м; l₂= 0,8 м; l₃= 1 м;

A₁= 5 см²; А₂= 6,8 см².

1.Так как продольная сила равна сумме отсекаемых сил ( ), то очевидно: N_l = F_l = 50 кН; N₂ = F₁ + F₂ = 70 кН; N₃ = F₁ + F₂ = 70 кН.

2. ;

;

.

3.

4.

Ответ: удлинение бруса составило 1,47 мм.

Задача № 8 Пример решения

По условию и результатам решения задачи № 2 раздела «Стати­ка», приняв найденные силы в стержнях за расчетные, определить для растянутого стержня диаметр круглого сечения, приняв R₁ = 160 МПа, а для сжатого стержня — сечение из двух равнополочных уголков, приняв без учета потери устойчивости R₂ = 80 МПа, коэффициент ус­ловий работы конструкций у_с = 1, коэффициент надежности (по назна­чению сооружения) у_п = 1.

Решив задачу № 2 из раздела «Статика», имеем:

N₁ = 22 кН — стержень растянут; N₂ = - 40,6 кН — стержень сжат.

1. Ввиду того, что коэффициенты у_с и у_п равны 1, расчетная формула N < RAy_cy_n примет вид N<=RA, откуда определяем необходимую площадь сечения стержней:

2. Подставляя, для растянутого стержня соответственно получим:

(мм²).

Т. к. для круга (мм).

Принимаем d= 14 мм.

3. Для сжатого стержня: 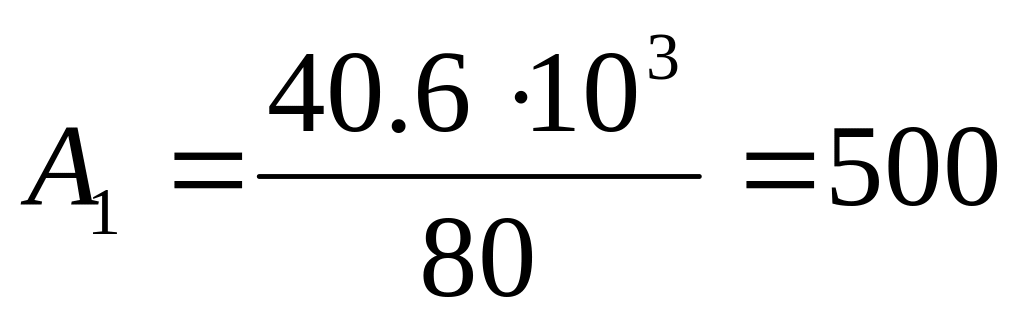(мм²) = 5 (см²).

4. Определяем площадь сечения одного уголка: 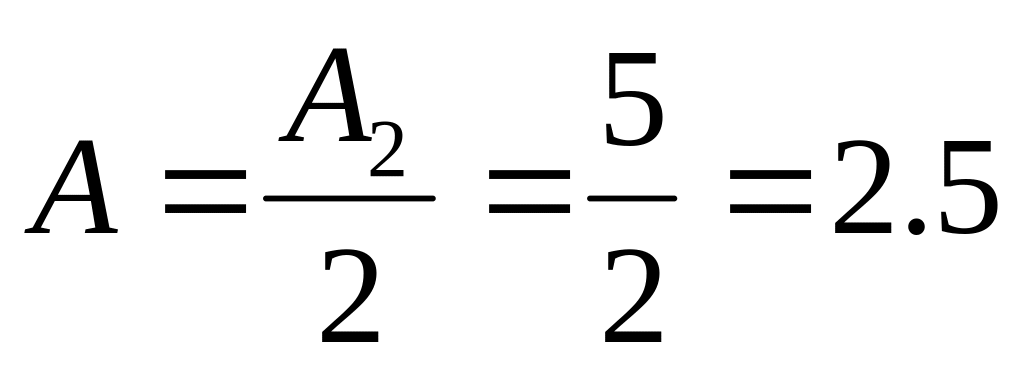(см ).

По таблице ГОСТ 8509-93 (приложения) подбираем номер сечения дву равнополочных уголков с площадью сечения А = 2,65 см² : 45x45x3.

Ответ: d= 14 мм; 2 уголка 45x45x3.