Будем считать углы дифракции φ отрицательными слева от центрального максимума и положительными справа. Обычно углы дифракции φ малы, поэтому .

Получаем: d tgφ₁ = λ; d tgφ₂ = 2λ или . Так как l₁ = l – l₂, получаем .

.

;

, то есть 103 штриха на 1 мм.

N = 2k_max + 1, где k_max получаем при φ = 90⁰;

k_max = ; N = + 1 = .

ЗАДАЧА 5. ПОЛЯРИЗОВАННЫЙ СВЕТ. ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА

Варианты 1 – 26

Кристаллическая пластинка, обладающая оптической активностью с постоянной вращения α, помещена между двумя николями – поляризатором и анализатором (рис. 5а и 5б). На поляризатор падает естественный или линейно поляризованный (в зависимости от варианта) свет, интенсивность которого I₀. После прохождения через поляризатор интенсивность света равна I₁, а после прохождения через анализатор – I₂. Угол между направлением колебаний светового вектора линейно поляризованной волны, подающей на поляризатор, и главной плоскостью поляризатора равен φ₁, а угол между главными плоскостями анализатора и поляризатора равен φ₂ (углы отсчитываются по часовой стрелке). Кристаллическая пластинка свет не поглощает, и толщина ее равна d. В николях теряется по 10 % проходящего через них света (неидеальные поляризатор и анализатор). Найти неизвестную величину, используя данные табл. 5. На рисунке по данным варианта показать углы φ₁, φ₂, φ₃ и Δφ, где φ₃ – угол поворота плоскости поляризации света в пластинке, Δφ – угол между волны, падающей на анализатор, и главной плоскостью анализатора (см. рис. 5б).

Рис. 5а. Прохождение света через систему поляризатор – вещество – анализатор (I - интенсивность света на выходе из кристаллической

пластинки)

Рис. 5б. Направление колебаний (состояние поляризации) световой волны при прохождении ее через систему

поляризатор – вещество – анализатор

Таблица 5

Данные для расчетов

Вариант	I0 – естест. или линейно поляриз.	φ1, град	I1/I0	φ2, град	I2/I0	α, град/мм	d, мм
1	Естест.	-	?	90	?	- 30	2
2	Линейно поляриз.	45	?	90	?	+ 30	2
3	Линейно поляриз.	0	?	0	?	+ 10	6
Окончание табл. 5
Вариант	I0 – естест. или линейно поляриз.	φ1, град	I1/I0	φ2, град	I2/I0	α, град/мм	d, мм
4	Линейно поляриз.	30	?	30	0,5	+ 30	?
5	Естест.	-	?	?	0,1	0	-
6	Естест.	-	?	60	0,3	+ 10	?
7	Естест.	-	?	90	0,2	?	3
8	Линейно поляриз.	60	?	?	0,11	- 15	2,5
9	Линейно поляриз.	0	?	5	0,8	?	1
10	Линейно поляриз.	15	?	?	0,05	+ 10	1,5
11	Естест.	-	?	0	0,15	- 10	?
12	Линейно поляриз.	?	?	90	0,7	- 20	5
13	Естест.	-	?	80	0,4	?	4
14	Линейно поляриз.	10	?	?	0,25	+ 20	2
15	Естест.	-	?	45	?	+ 25	3
16	Естест.	-	?	?	0,08	+ 30	1
17	Естест.	-	?	30	0,35	+ 10	?
18	Линейно поляриз.	0	?	0	?	- 15	2,5
19	Линейно поляриз.	70	?	45	0,01	?	1,5
20	Линейно поляриз.	0	?	60	0,7	- 30	?
21	Линейно поляриз.	30	?	30	?	+ 30	1
22	Линейно поляриз.	45	?	45	?	+ 45	1
23	Линейно поляриз.	60	?	60	?	+ 60	1
24	Естест.	-	?	30	0,3	- 10	?
25	Естест.	-	?	45	0,3	- 20	?
26	Естест.	-	?	90	?	+ 30	1,5

Пример решения задачи № 5 (вариант № 26)

Дано:

На систему падает

естественный свет

φ₂ = 90⁰ (рис. 5в)

α = 30 град/мм

d = 1,5 мм

k = 10 % = 0,1

Найти: 1) I₁/I₀ - ?

Решение:

1. Для идеального поляризатора I 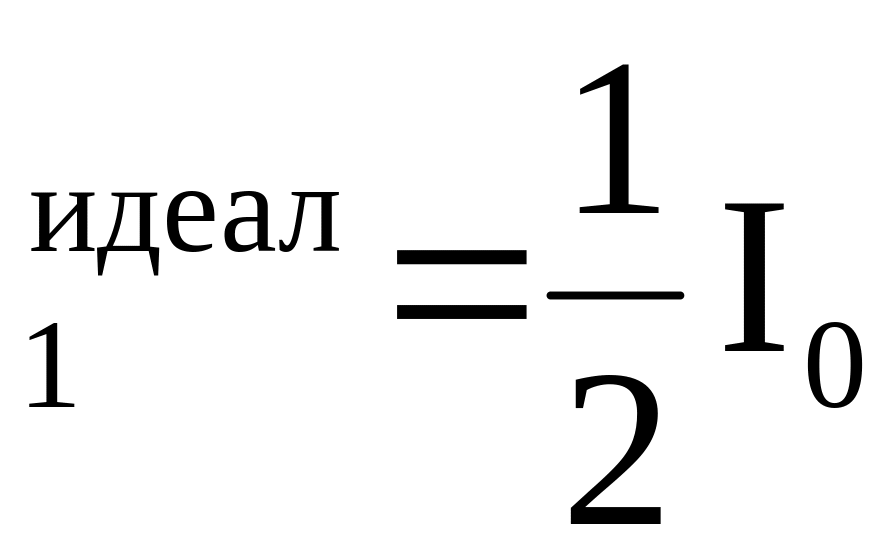, а с учетом 10 % поглощения

2) I₂/I₀ - ?

2. Угол поворота плоскости поляризации линейно поляризованного света, прошедшего через оптически активное вещество, определяется по формуле

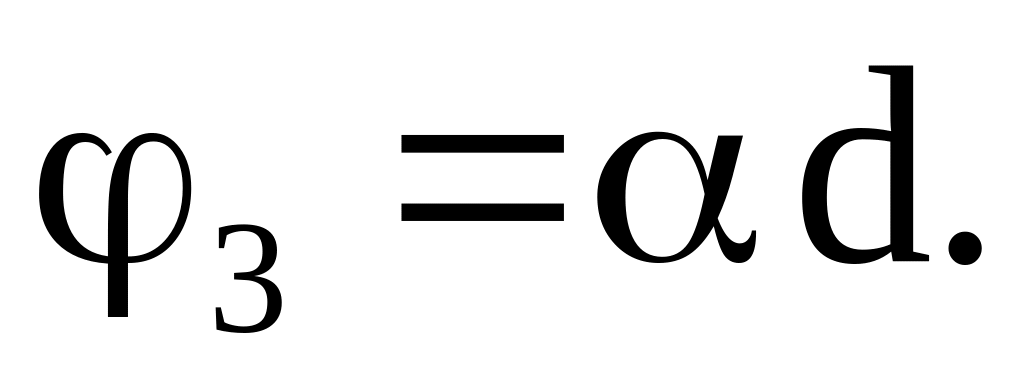
В нашем случае

φ₃ = 30 град/мм ∙ 1,5 мм = 45⁰

Δφ = φ₂ – φ₃ = 90⁰ – 45⁰ = 45⁰.

П

Рис. 5в. Ориентация световой волны относительно плоскостей поляризатора и анализатора

о закону Малюса для идеального анализатора

, а в данном случае

. Так как то

;

.