Инженерная и
компьютерная графика
Раздел
Начертательная
геометрия
Практикум по решению задач
Оглавление
Тема 1: ВИДЫ ПРОЕЦИРОВАНИЯ 5
Задача 1. 5
Задача 2. 6
Задача 3. 8
Задача 4. 10
Задача 5. 11
Тема 2: ПРОЕКЦИИ ТОЧКИ 13
Задача 6 13
Задача 7. 14
Задача 8. 16
Тема 3: ПРОЕКЦИИ ПРЯМОЙ ЛИНИИ 17
Задача 9. 17
Задача 10. 18
Задача 11. 19
Задача 12. 20
Задача 13. 21
Задача 14. 22
Задача 15. 22
Тема4: ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПРЯМОЙ 23
Задача 16. 23
Задача 17. 23
Задача 18. 24
Задача 19. 24
Тема 5: ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ 25
Задача 20. 25
Задача 21. 26
Задача 22. 28
28
ТЕМА 6: ПРОЕКЦИИ ПЛОСКОСТИ 29
Задача 23. 29
Задача 24. 32
Задача 25. 33
Задача 26. 34
Задача 27. 35
ТЕМА 7: ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ, ПРЯМОЙ И ПЛОСКОСТИ 36
Задача 28. 36
Задача 29. 37
Задача 30. 37
Задача 31. 38
Задача 32. 39
Задача 33. 40
Задача 34. 40
Тема 8: Взаимное расположение двух плоскостей 42
Задача 35. 42
Задача 36. 42
Задача 37. 43
Задача 38. 45
Задача 39. 47
Задача 40. 48
Задача 41. 49
ТЕМА 9: МНОГОГРАННИКИ 49
Задача 42. 49
Задача 43. 50
Задача 44. 51
Задача 45. 53
Задача 46. 54
Задача 47. 56
Задача 48. 56
ТЕМА 10: КРИВЫЕ ЛИНИИ 57
Задача 49. 57
Задача 50. 58
Задача 51. 59
Задача 52. 60
Задача 53. 62
Задача 54. 63
Задача 55. 63
Задача 56. 64
Задача 57. 65
Задача 58. 66
Задача 59. 66
Задача 60. 67
Задача 61. 68
ТЕМА 11: ПОВЕРХНОСТИ 69
Задача 62. 69
Задача 63. 70
Задача 64. 71
Задача 65. 72
Задача 66. 73
Задача 67. 75
ТЕМА 12: МЕТОДЫ ПРЕОБРАЗОВАНИЯ ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ 76
Задача 68. 76
Задача 69. 77
Задача 70. 78
Задача 71. 79
Задача 72. 80
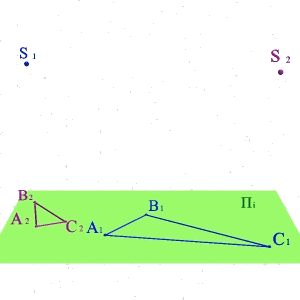
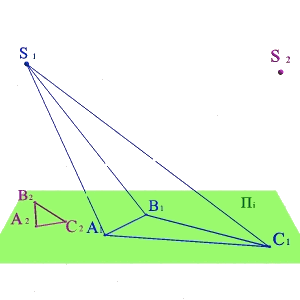
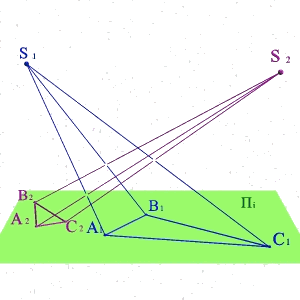
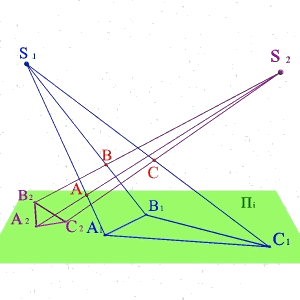
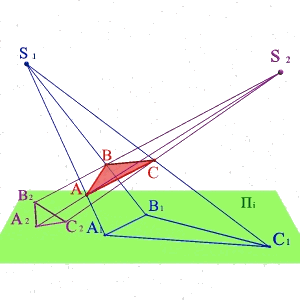
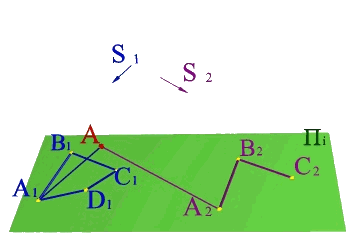
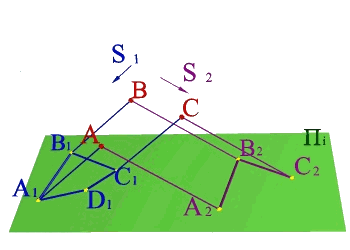
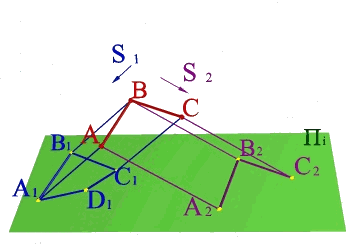
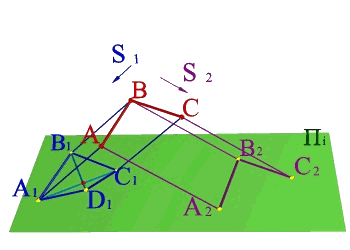
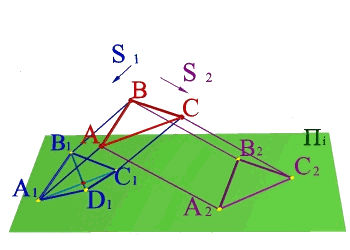
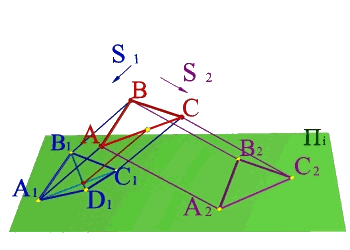
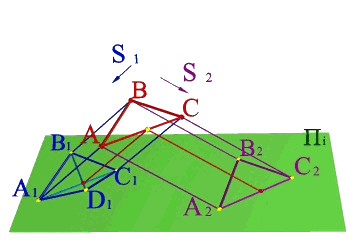
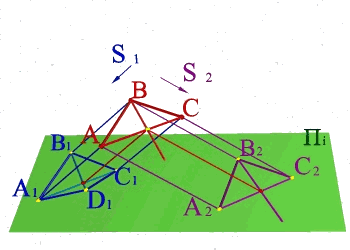
Тема 1: виды проецирования Задача 1.
|
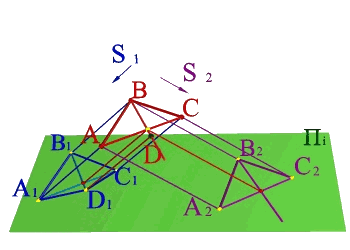
По двум центральным проекциям треугольника АВС определить его пространственное положение. Для решения задачи необходимо ознакомиться с методом центрального проецирования и выполнить обратные действия: 1) Из центра S1 провести проецирующие лучи к проекциям А1 В1 С1 ; 2)Из центра S2 провести проецирующие лучи к проекциям А2 В2 С2 ; 3) Точки А, В, С находятся на пересечении лучей S1А1 и S2А2 ,S1В1 и S2В2, S1С1 и S2С2 соответственно и определяют положение плоскости заданной треугольником в пространстве. |
|
|
|
|
|
|
|
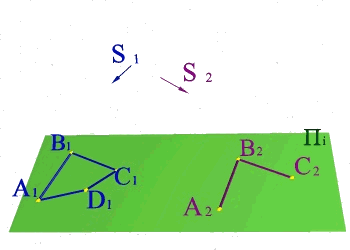
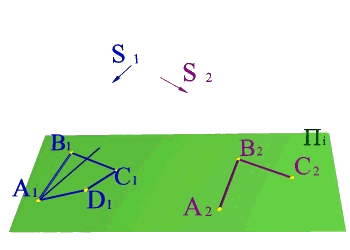
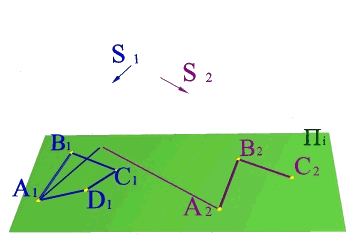
Задача 2.
|
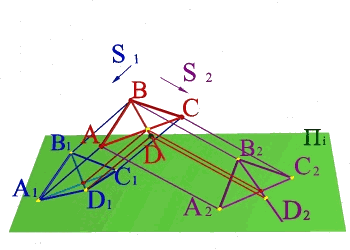
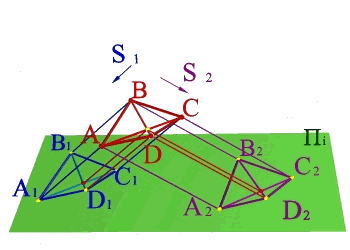
По имеющимся параллельным проекциям четырехугольника АВСD построить пространственное положение четырехугольника АВСD и построить недостающую проекцию его вершины D. Для решения задачи необходимо ознакомиться с методом параллельного проецирования и знать его свойства: 1.Если прямые пересекаются, то пересекаются и проекции этих прямых; 2. Если точка принадлежит прямой, то и проекции точки принадлежат проекциям прямой; 3. Для построения проекции прямой линии необходимо найти проекции двух её точек. Решение: 1. Проводим проецирующие лучи из известных проекций, находим пространственное положение точек А,В,С; 2. Вводим диагонали четырехугольника: А1С1, В1D1, АС и А2С2; 3. Находим с помощью проецирующих лучей точку пересечения диагоналей на АС и её проекцию на А2С2; 4. Через В и точку пересечения диагоналей проводим прямую на которой с помощью проецирующих лучей определяем положение точки D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
