Лекция 4. Метод зейделя

4.1. Условия сходимости процесса Зейделя

Метод Зейделя представляет собой некоторую модификацию метода последовательных приближений. В методе Зейделя при вычислении (k + 1) приближения неизвестного x_i учитываются уже найденные ранее (k+1) приближение неизвестных.

Пусть дана линейная система

(4.1)

Выбираем произвольно начальное приближение корней и подставляем в первое уравнение системы (4.1)

,

полученное первое приближение подставляем во второе:

.

Полученные первые приближения х₁⁽¹⁾ и х₂⁽¹⁾ подставляем в третье уравнение системы (4.1)

и т. д.

.

Аналогично строим вторые и третьи итерации.

Таким образом, предполагая, что k приближение корней х^k_i известно, по методу Зейделя строим (k + 1) приближение

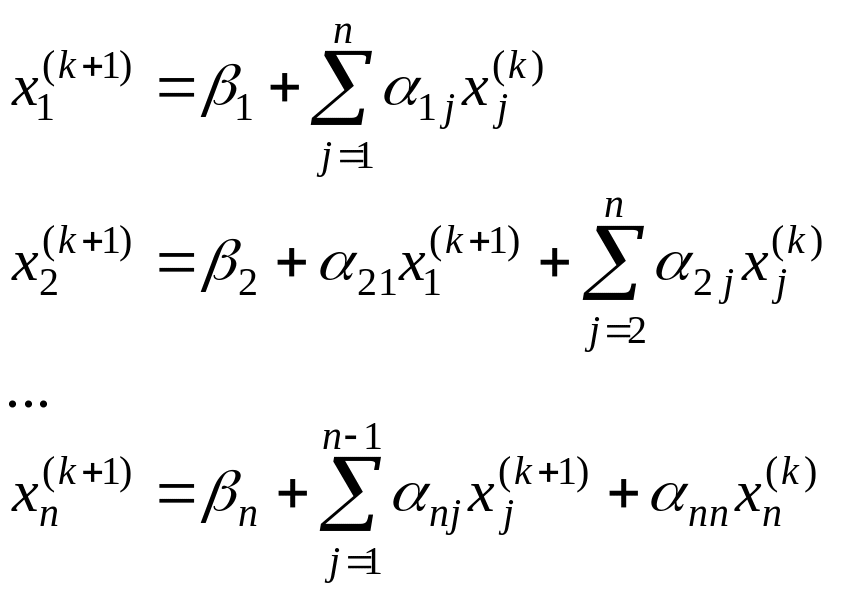
где k = 0, 1, 2, …, n.

Пример. Методом Зейделя решим систему:

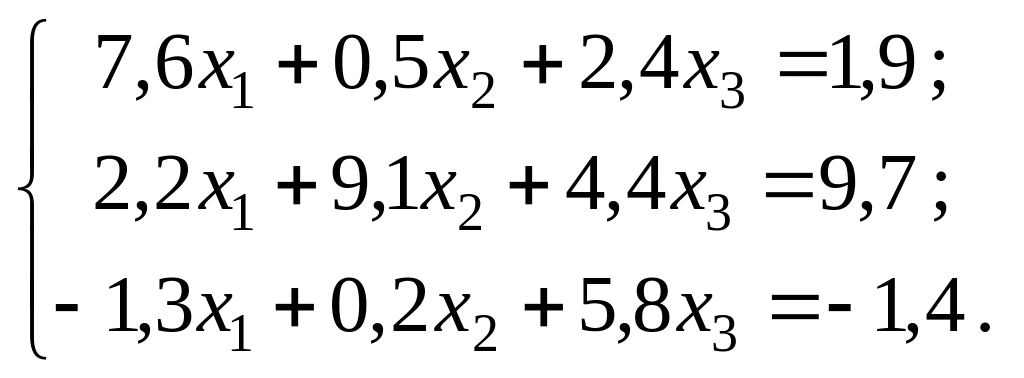
1. Приведем систему к нормальному виду:

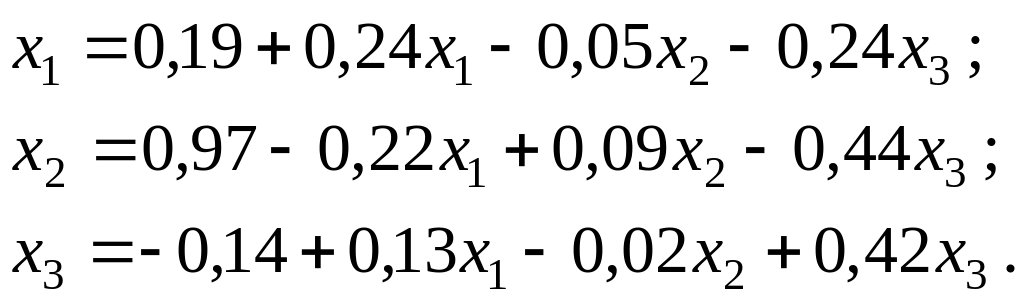
2. За нулевые значения возьмем соответствующие значения свободных членов

.

3. Строим итерации по методу Зейделя

Второе приближение

И т.д.

№ итерации
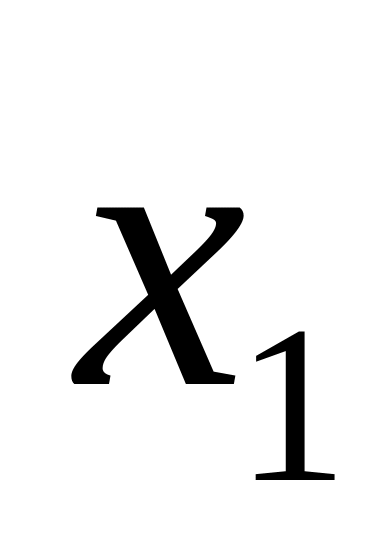
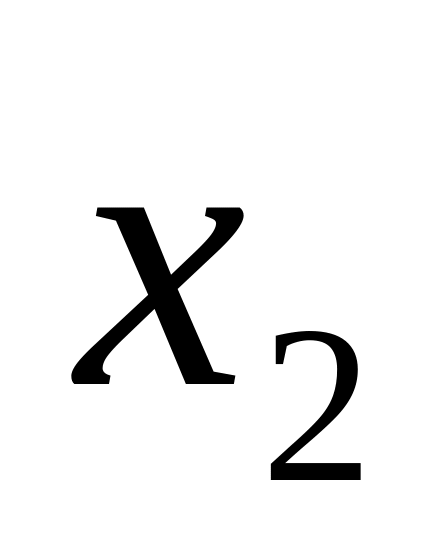
0	0,19	0,97	-0,14
1	0,2207	1,0703	-0,1915
2	0,2354	1,0988	-0,2118
3	0,2424	1,1088	-0,2196
4	0,2454	1,1124	-0,2226
5	0,2467	1,1138	-0,2237
6	0,2472	1,1143	-0,2241
7	0,2474	1,1145	-0,2243
8	0,2475	1,1145	-0,2243

Построенный процесс заканчивается, когда с заданной степенью точности получаем одинаковые значения в двух итерациях подряд.

;

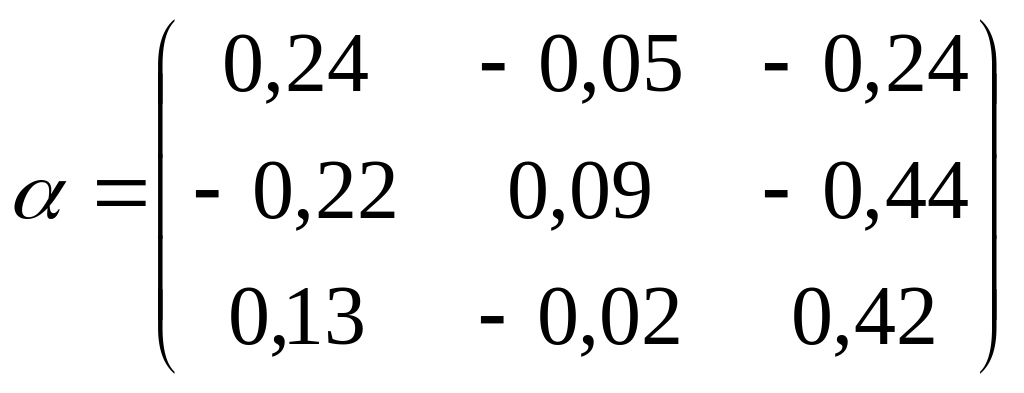Процесс Зейделя для линейной системы Х =  + Х также, так и процесс последовательных приближений, сходится к единственному решению при любом выборе начального приближения, если какая-нибудь из норм матрицы  меньше единицы. То есть

либо

,

либо

.

Процесс Зейделя сходится к единственному решению быстрее процесса простой итерации.

4.2. Оценка погрешности процесса Зейделя

Пусть дана линейная система

x =  + х ,

где x_i – точное значение корней линейной системы, x_i^(k) – k приближение, вычисленное по методу Зейделя. Тогда оценка погрешности этого метода делается по формуле

; .

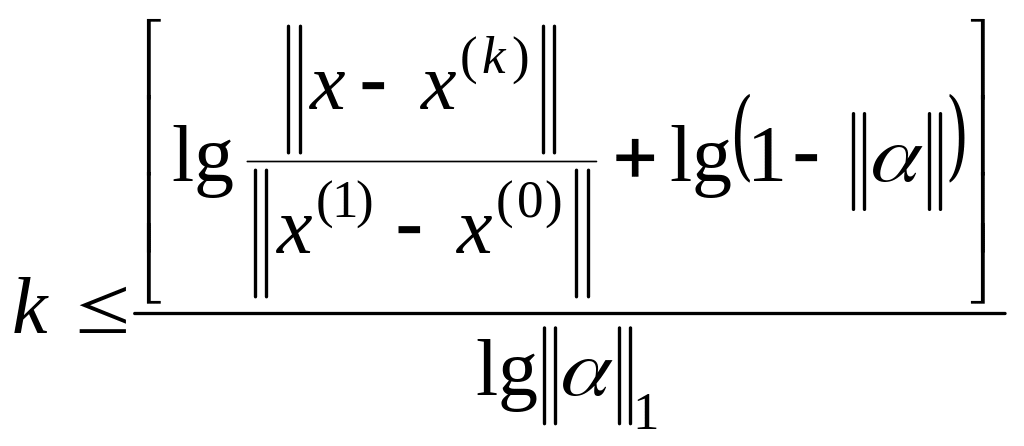Пример. Подсчитать, сколько итераций по методу Зейделя необходимо выполнить, чтобы с точностью до 10^-4 найти корни системы.

Решение:

; ;

.

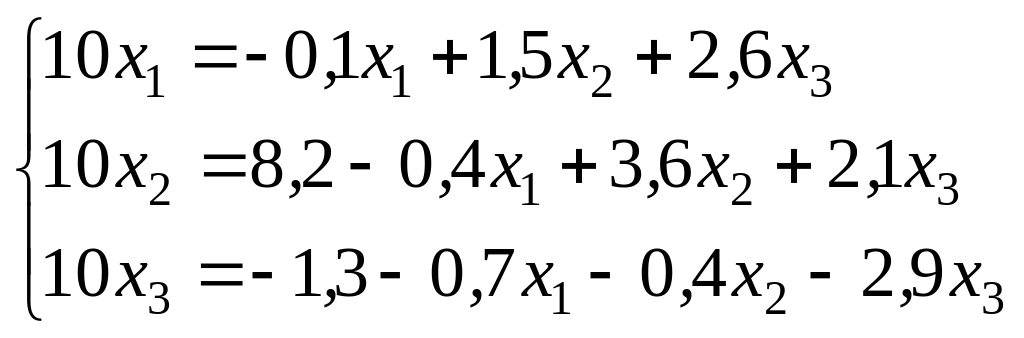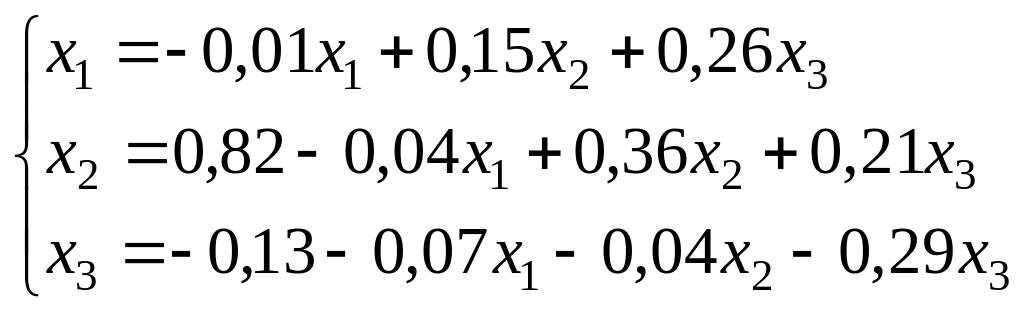Значит

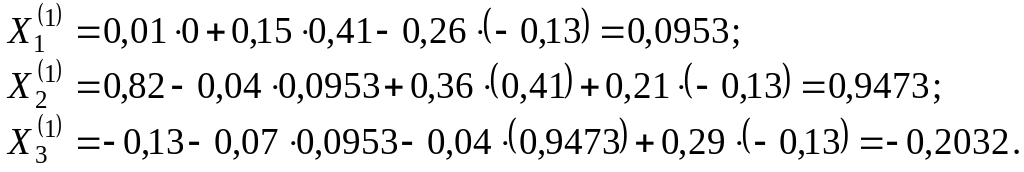
Или

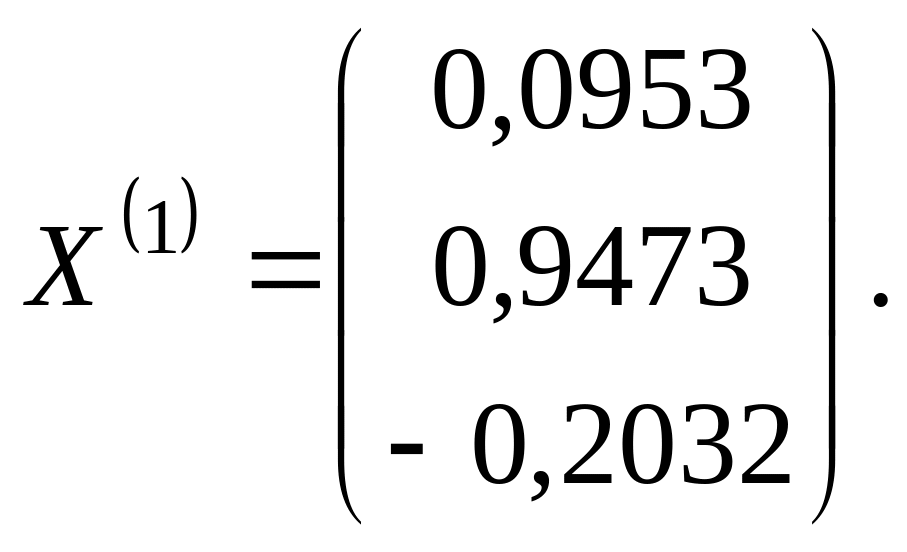
Имеем :

,

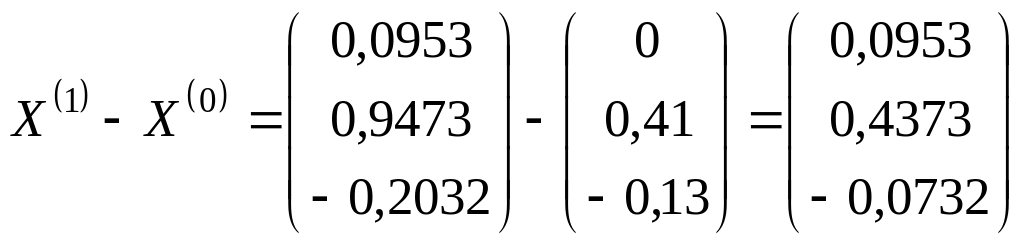т.е.

,

по формуле (3.8) определяем

,

,

.

4.3. Приведение системы линейных уравнений к виду, удобному для итераций

Процессы последовательных приближений и метод Зейделя для линейных систем х =  +  сходятся к единому решению, независимо от выбора начального вектора, если

или

.

Таким образом, для сходимости вышеуказанных итерационных процессов достаточно, чтобы значения элементов _ij при i  j были небольшими по абсолютной величине. Это равносильно тому, что если для линейной системы АХ = В модули диагональных коэффициентов каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов), то итерационные процессы для этой системы сходятся, т.е. мы имеем систему

.

Причем, если то процессы последовательных приближений и Зейделя для данной системы сходятся. Применяя элементарные преобразования, линейную систему АХ = В можно заменить такой эквивалентной системой Х = р + Х, для которой условия сходимости будут выполнены.