1.2. Абсолютные и относительные погрешности
Принципиальная трудность работы с вещественными числами заключается в том, что любая переменная в памяти ЭВМ может принимать лишь конечное число значений, поэтому вещественные числа не могут быть представлены в компьютере точно. Числа записываются в форме с плавающей запятой.
При этом отдельно хранится мантисса М. Число М по абсолютной величине не превосходит 1 и порядок P, значит, пара (Р,М) задает вещественное число
В ЭВМ, как правило, а = 2 или a = 16. Для записи мантиссы используется фиксированное число k, т.е.
,
где ММ – целое число и
.
Диапазон изменения порядка тоже ограничен:
.
Значит, представление чисел в компьютере обладает следующими свойствами:
Абсолютная погрешность равна абсолютной величине разности точного числа и приближенного
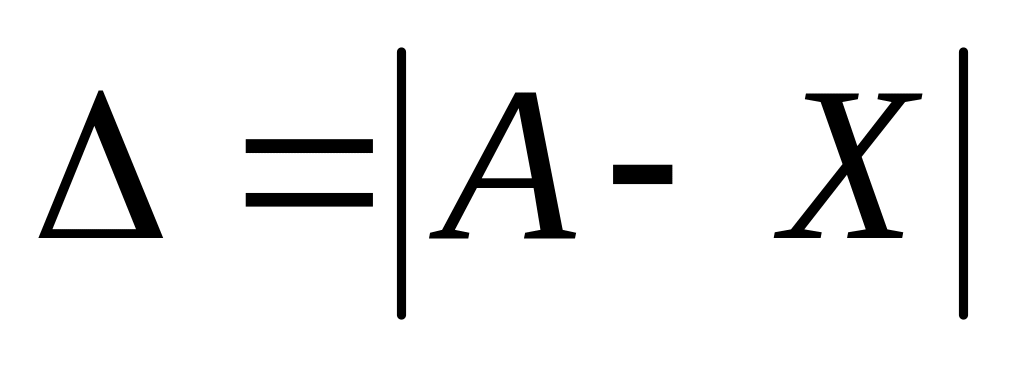.Относительная погрешность равна отношению абсолютной погрешности к точным значениям
.Невозможно представить очень большие по модулю и очень малые («нулевые») числа. Произвольное вещественное число, попадающее в допустимый интервал, может быть написано с некоторой погрешностью. Относительная погрешность в этом случае примерно постоянна и равна
.
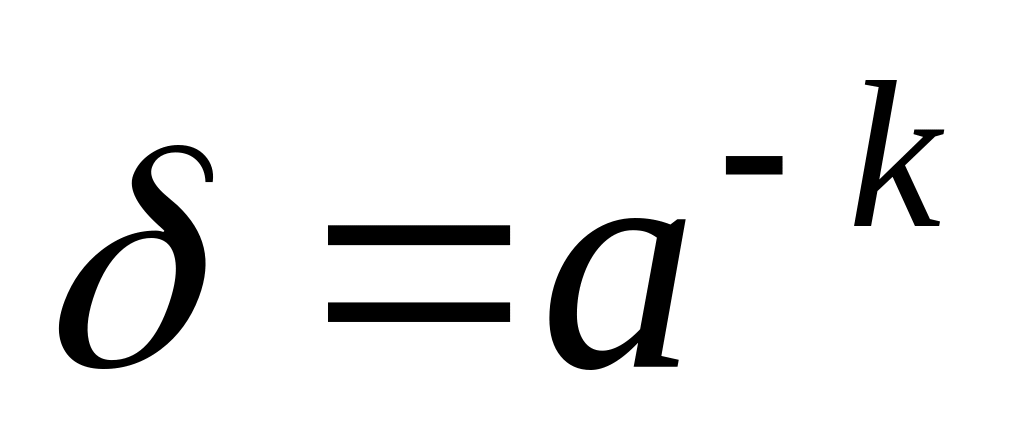Рассмотрим ошибки вычислений, связанных с вычитанием близких чисел – действие, приводящее к потере точности
,
или
.
Следующий источник ошибок – суммирование слагаемых с различным порядком сложения:
55,55 + 0,001 + 0,001 + … + 0,001 .
Мы не можем хранить пятую цифру, т.е. результат будет 55,55, следовательно, останется без изменений. А если сначала сложить 100 х 0,001 = 0,1 получим 55,61. Поэтому суммирование чисел необходимо производить в порядке возрастания слагаемых.
1.3. Понятие о системе линейных уравнений
В общем виде система m линейных уравнений с n неизвестными записывается так:
(1.1)
Уравнения
системы считаются пронумерованными:
первое, второе,
-
е,
–
неизвестные,
–
коэффициенты при неизвестных.
Коэффициент
при неизвестном
в i
– уравнении обозначается через
,
j
– номер
неизвестного.
Кратко система (1.1) может быть записана:
,
(i
= 1, 2, …,
m).
(1.2)
Решением
системы линейных уравнений называется
любая совокупность чисел
,
которая, будучи подставленной на место
неизвестных
в уравнение данной системы, обращает
все эти уравнения в тождества. Система
(1.1) – совместная, если она имеет решение.
Если система не имеет решений, то она
называется несовместной
или противоречивой.
Совместная система линейных уравнений может иметь одно или несколько решений. Она называется определенной, если имеет одно решение, и неопределенной, если имеет больше одного решения.
Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если они обе несовместны или совместны и имеют одни и те же решения.
Пусть дана определенная система n линейных уравнений (1.1). Пользуясь матричными обозначениями её, можно заменить следующим:
,
(1.3)
где матрица системы
;
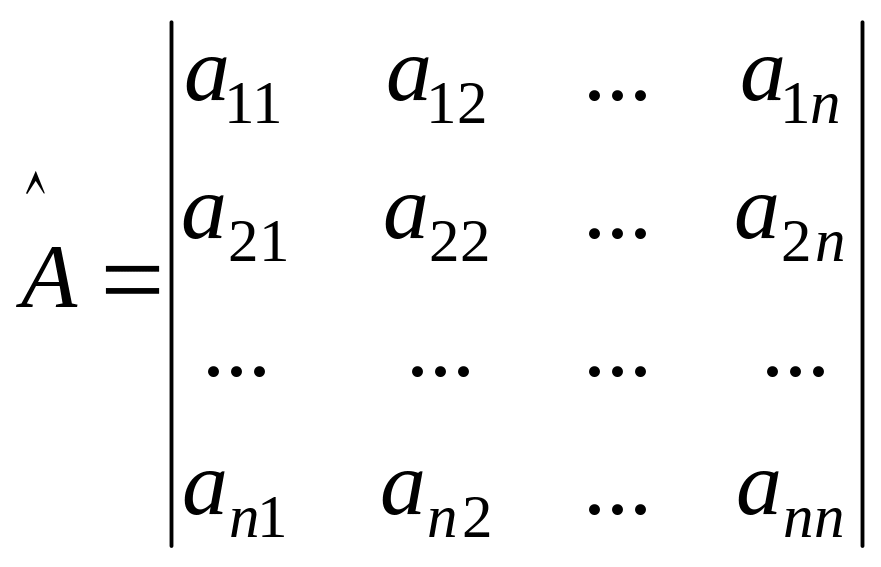(1.4)
вектор-столбец неизвестных
;
(1.5)
вектор-столбец свободных членов
.
(1.6)