Образцы выполнения контрольных работ Контрольная работа № 5

Вычислить значение интеграла

, , а = 0, b = 0, .

Выберем формулу для приближенного вычисления заданного определенного интеграла. Для чего найдем по формулам (9.4), (9.6), (9.10) число n точек разбиения отрезка [0,1] на частичные, которые обеспечат требуемую точность при вычислении по формулам прямоугольников, трапеций и парабол соответственно. А затем остановимся на той из приближенных формул, для которой число n будет наименьшим.

Чтобы воспользоваться формулами (9.4), (9.6), (9.10), вычислим и оценим первую, вторую и четвертую производные подынтегральной функции на отрезке [0,1]:

, ,

,

и так как функция f(x) и ее производные убывают на отрезке [0,1], то

,

,

.

Найдем n. Для формулы прямоугольников из (9.4) получаем

.

Для формулы трапеций из (9.6) получаем

, .

Для формулы парабол из (9.10) получаем

; .

Таким образом, наименьшего объема вычислений при одинаковой точности потребует формула парабол (9.8) – n = 2m = 8 (n должно быть четным), применяя которую и вычислим приближенно заданный интеграл.

По числу n = 2m = 8 найдем шаг интегрирования .

Составим таблицу (табл.1.) значений подынтегральной функции в точках x_i = ih, , записывая ординаты с четными и нечетными номерами в разные столбцы. В последней строке таблицы запишем результаты суммирования по этим столбцам. Вычисление будем вести с четырьмя знаками после запятой, а окончательный ответ округлим до трех знаков после запятой.

Применяя формулу парабол (9.8), получим

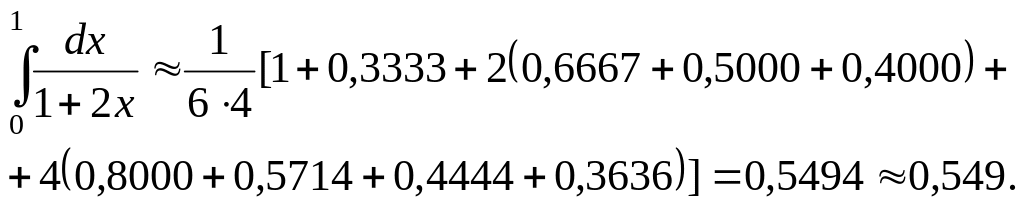
Вычислим заданный интеграл по формуле Ньютона–Лейбница

.

Итак, требуемая точность вычислений достигнута.

Таблица 1

i	xi=a+ih,	1+2хi	Значения уi=1/(1+2хi)
			При i=0, i=8	При четном i	При нечетном i
0	0	1,0
	0,125	1,250			0,80
	0,25	1,50		0,6667
	0,375	1,750			0,5714
	0,50	2,00		0,50
	0,625	2,250			0,4444
	0,750	2,50		0,40
	0,875	2,750			0,3636
	1,0	3,0	0,3333
Суммы			1,3333	1,5667	2,1794

Контрольная работа № 6

Пусть дано:

; у(0)=1; x [1,2] .

Шагом интегрирования h = 0,2 отрезок [0,1] разбивается на пять равных частей точками х₀ = 0, х₁ = 0,2, х₂ = 0,4, х₃ = 0,6, х₄ = 0,8, х₅ = 1,0.