Приближение линейными сплайнами

Пусть m = 1 .

Тогда общее число Q свободных параметров равно 2N .

Поставим вопрос о построении сплайна совпадающего с функцией f(x) в точках x₀, x₁,…, x_n .

Получим систему уравнений

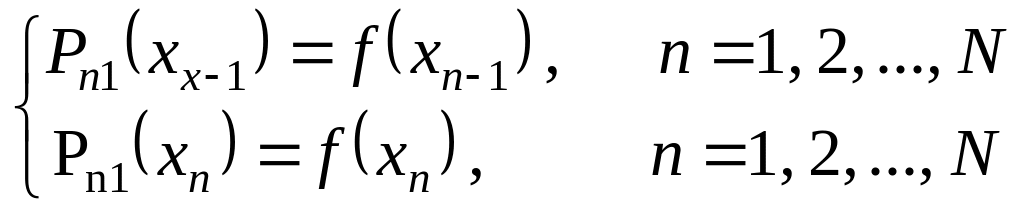
Эта система распадается на системы уравнений относительно коэффициентов отдельных многочленов

,

отсюда находим

Многочлен P_n1(x) является многократно рассматривавшимся интерполяционным многочленом первой степени с узлами интерполяции x_n-1, x_n.

Широкое распространение сплайнов во многом вызвано тем, что они являются в определенном смысле наиболее гладкими функциями среди функций, принимающих заданные значения. Сплайны степени выше первой в случае гладкой f(x) хорошо приближают не только саму функцию, но и ее производные.

Лекция 9. Численное интегрирование функций

Известно, что не для всякой функции ее первообразная выражается через элементарные функции. В этих случаях вычисление определенных интегралов по формуле Ньютона-Лейбница затруднительно и применяются различные методы приближенного вычисления определенных интегралов. Пользуясь геометрическим смыслом определенного интеграла, рассмотрим три приближенных формулы, с помощью которых численное интегрирование проводится с любой степенью точности.

9.1. Постановка задачи

Пусть на отрезке [a,b] задана непрерывная функция y = f(x). Требуется вычислить приближенное значение определенного интеграла

(9.1)

Е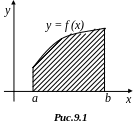 сли f(x) ≥ 0 при a ≤ х ≤ b,то интервал будет численно равен площади так называемой криволинейной трапеции, ограниченной графиком функции y = f(x), прямыми х = a, х = b и осью Ох (рис.9.1).

Воспользуемся этой интерпретацией определенного интеграла.

Разобьем отрезок [a,b] точками a = х₀ , х₁, ..., х_n = b на n равных частей длины , так что x_i = a + ih, .

Величина h называется шагом интегрирования. Обозначим через у₀ , у₁, …, у_n значения функции y = f(x) в точках х₀ , х₁ ...., х_n соответственно, то есть y_i = f(x_i), .

9.2. Формула прямоугольников

Заменим площадь криволинейной трапеции aАВb (рис. 9.2), численно равную интегралу (9.1), на сумму площадей левосторонних или правосторонних прямоугольников, то есть на y₀h + y₁h + … + y_n-1 h или y₁h + y₂h + … + y_nh. Тогда интеграл (9.1) приближенно выражается любой из формул:

, (9.2)

(9.2')

Это формулы левосторонних и правосторонних прямоугольников.

Ч ем больше число n, тем меньше ошибка, совершаемая при вычислении на отрезке [a,b], то и для погрешности R_n формул прямоугольников справедлива следующая оценка:

(9.3)

где . Если задана точность вычислений ε, то из (3) можно найти число разбиений n отрезка [a,b], которое обеспечит эту точность

. (9.4)

9 .3. Формула трапеций. Естественно ожидать более точное значение интеграла (9.1), если данную кривую y = f(x) заменить не ступенчатой, как это было в формуле прямоугольников, а вписанной ломаной (рис. 9.3). Тогда площадь криволинейной трапеции aABb заменится суммой площадей прямолинейных трапеций, ограниченных сверху хордами АА₁, А₁А₂, …, А_n-1B. Так как площади этих трапеций соответственно равны

то для интеграла (1) получаем приближенную формулу

(9.5)

Это формула трапеций. Число n произвольно, но чем оно больше, тем с большей точностью будет получено значение интеграла (9.1). Если f"(x) существует и ограничена на отрезке [a,b], то погрешность R_n формулы (9.5) оценивается неравенством

, (9.6)

г де . Если задана точность вычислений ε, то из (9.6) можно найти число разбиений n отрезка [a,b], обеспечивающее эту точность

. (9.7)

9.4. Формула парабол (Формула Симпсона). Разделим отрезок [a, b] на четное число равных частей n = 2m. Площадь криволинейной трапеции, соответствующей первым двум отрезкам [х₀, х₁] и [х₁, х₂] и ограниченной заданной кривой y = f(x), заменим площадью параболической трапеции, которая ограничена параболой, проходящей через три точки М₀(х₀, у₀), М₁(х₁, у₁), М₂(х₂, у₂), и имеющей ось, параллельную оси Оу (рис. 9.4). Аналогичным образом поступим и для других пар отрезков [х₂, х₃], [х₃, х₄], …, [х_2m-2, х_2m-1], [х_2m-1, х_2m]. Площади построенных параболических трапеций соответственно равны

, , …, ,

а их сумма даст приближенное значение интеграла (9.1)

(9.8)

Это формула Симпсона. Здесь число 2m точек деления отрезка [a,b] произвольно, но чем больше это число, тем точнее значение интеграла (9.1). Если f"(x) существует и ограничена на отрезке [a,b], то для погрешности R_n формулы (9.8) справедлива следующая оценка:

, (9.9)

где . Если задана точность вычислений ε, то из (9.9) можно найти число разбиений 2m = n отрезка [a,b], которое обеспечит эту точность

. (9.10)

ЗАМЕЧАНИЕ. В связи с трудностями оценки четвертой производной подынтегральной функции f(x), погрешность R_n совершаемую при вычислении определенного интеграла (9.1), по формуле (9.8), можно оценить по правилу Рунге

,

где J_n и J_2n – приближенное значение интеграла, вычисленное по формуле парабол, соответственно с шагом h и . За приближенное значение J интеграла (9.1), вычисленное по формуле парабол с поправкой Рунге, принимают

.