Тема 2. Сложные проценты

Методические указания.

Формула наращения по сложным процентам:

Если начисления процентов по периодам различны, то вычисление S осуществляется по формуле:

Формула наращения по сложным процентам при начислении процентов m раз за год:

Эффективная ставка показывает, какая годовая ставка сложных процентов даст такой же результат, как m – разовое начисление процентов в год по ставке i/m:

Если эффективная ставка начисления сложных процентов (за месяц, квартал, полугодие) известна, то можно рассчитать номинальную годовую ставку по формуле:

.

Математическое дисконтирование (учет) про сложной ставке процентов:

где νⁿ – дисконтный или учетный множитель.

Если проценты начисляются m раз в году, то приведенная к началу операции сумма определится выражением:

Дисконтирование по банковской ставке сложных процентов осуществляется по формуле

где d_сл – сложная годовая учетная ставка.

Дисконт в этом случае равен

Формулы для определения процентной ставки i и продолжительности операции n (mn) получаются из предыдущих формул:

если проценты начисляются раз в году;

если проценты начисляются m раз в году.

Формулы показывают, что величина любого из параметров S, P, n, i может быть определена по известным трем остальным.

Примеры решения задач:

Пример 2.1. Сумма, равная 600 тыс. руб., дается в займы на 3 года под 15% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

Решение:

1. Сложные проценты:

Доход равен 912 – 600 = 312 тыс. руб.

2. Простые проценты:

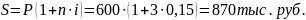
Доход равен 870 – 600 = 270 тыс. руб.

Пример 2.2. Сумма, равная 600 тыс. руб., инвестируется на 4 месяца под 15% годовых. Сравнить наращенные суммы и суммы процентов за этот срок, используя простую и сложную процентные ставки.

Решение:

1.Сложные проценты:

Сумма процентов 628,6 – 600 = 28,6 тыс. руб.

2. Простые проценты:

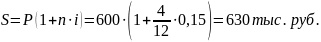
Сумма процентов 630– 600 = 30 тыс. руб.

Итак, если срок наращения меньше интервала наращения, то выгоднее наращивать капитал по простым процентам.

Пример 2.3. Найти сумму долга в 20 млн. руб. через 8 месяцев, 200 дней, 4 года, 8 лет по сложным годовым ставкам 10% и 15%.

Решение:

Расчетная формула:

1. i = 10%:

2. i = 15%:

Сумма долга растет с увеличением и процентной ставки, и числа лет начисления.

Пример 2.4. В банк на депозит положена сумма в 5 млн. руб. на 2 года по ставке процента 20% годовых сложных. Определить наращенные суммы при ежемесячном, ежеквартальном, полугодовым и годовым начислением процентов.

Решение:

Расчет производится по формуле:

где m – количество начислений процентов в году ( 12, 4, 2, и 1).

Итак, чем чаще капитализируются процентные начисления, тем больше сумма наращения.

Пример 2.5. На сумму 5 млн. руб. начислить проценты по непрерывной ставке  =10% годовых 5 лет.

Если число начислений процентов в году m  , то формула наращения принимает вид:

,

где  - непрерывная ставка годового процента.

Решение:

млн. руб.

Пример 2.6. Предприятию через 3 года будет выплачена сумма 2 млн. руб. Определить ее современную стоимость при условии, что годовая ставка сложных процентов составляет 10% годовых, а начисление процентов осуществляется ежеквартально.

Пример 2.7. Рассчитать эффективные ставки процентов за 1 год при ежегодном, полугодовом, квартальном, ежемесячном и ежедневном начислении процентов, если номинальная годовая ставка j = 20%.

Решение:

Формула для расчета эффективной ставки имеет вид:

С учетом этой формулы, имеем:

1. m = 1 (ежегодное начисление) i_эфф = (1+ 0,2 / 1)¹ – 1 = 0,2 ( 20% );

2. m = 2 (полугодовое начисление) i_эфф = (1+ 0,2 / 2)² – 1 = 0,21 ( 21% );

3. m = 4 (полугодовое начисление) i_эфф = (1+ 0,2 / 4)⁴ – 1 = 0,2155 ( 21,55% );

4. m = 12 (ежемесячное начисление) i_эфф = (1+ 0,2 / 12)¹² – 1 = 0,2194 ( 21,94% );

5. m = 365 (ежедневное начисление) i_эфф = (1+ 0,2 / 365)³⁶⁵ – 1 = 0,2213 ( 22,13% ).

Пример 2.8. Найти номинальную годовую процентную ставку, если эффективная годовая ставка при ежеквартальном начислении процентов равна 10,38%.

Решение:

Номинальная ставка рассчитывается по следующей формуле:

Пример 2.9. Найти номинальную годовую процентную ставку, если квартальная эффективная ставка равна 3 %.

Решение:

Уравнение эквивалентности ставок имеет вид:

Пример 2.10. Какую ставку должен назначить банк, чтобы при годовой инфляции в 9%, реальная ставка оказалась 6%? Банк при годовом темпе инфляции в 9% рассчитывает получить реальную ставку 7%. Как должна быть скорректирована ставка процента?

Решение:

Скорректированная банковская ставка r (брутто-ставка) находится из выражения:

где i – реальная ставка; h – темп инфляции. Из формулы находим:

Расчет параметров финансовых операций с элементарными потоками средствами Excel

ППП Excel содержит группу из 52 функций для автоматизации финансовых расчетов. Для расчета операций с элементарными потоками используются следующие функции (Табл.2.1):

Таблица 2.1. Функции Excel для анализа потока платежей.

Наименование функции	Формат функции
БС (англоязычная версия (а.в.) FV)	БС(ставка;кпер;плт;пс;[тип])
КПЕР (а.в.) NPER)	КПЕР(ставка;плт;пс;бс;[тип])
СТАВКА (а.в.) RATE)	СТАВКА(кпер;плт;пс;бс;[тип])
ПС (а.в.) PV)	СТАВКА(ставка;кпер;плт;бс;[тип])
ПЛТ (а.в.) PMT)	ПЛТ(ставка;кпер;пс;бс;[тип])
БЗРАСПИС (а.в.) FVSHEDULE)	БЗРАСПИС(сумма;массив ставок)
НОМИНАЛ (а.в.) NOMINAL)	НОМИНАЛ(эф_ставка;кол_пер)
ЭФФЕКТ (а.в.) EFFECT)	ЭФФЕКТ(ном_ставка;кол_пер)

Аргументы функций:

• СТАВКА – процентная ставка (норма доходности или цена заемных средств i);

• КПЕР – срок (число периодов n ) проведения операции;

• ПЛТ – величина периодической выплаты (R);

• ПС – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей (P);

• БС – будущее значение (S);

• [ТИП] – определяет момент выплаты (1 – начало периода, 0 или опущен – конец периода);

• БЗРАСПИС – позволяет рассчитать будущее значение потока платежей при плавающей процентной ставке;

Для получения корректного результата при работе функций КПЕР() и СТАВКА() аргументы ПС и БС должны иметь противоположные знаки.

Функции НОМИНАЛ и ЭФФЕКТ удобно использовать при сравнении операций с различными периодами начисления процентов. При этом доходность финансовой операции измеряется эффективной процентной ставкой.

Пример 2.11. Определить будущую величину вклада в 300 000 ден.ед., помещенного в банк под 10% годовых, если начисления процентов осуществляются: раз в году; раз в полгода; раз в квартал; раз в месяц.

Решение. Разместим исходные данные в таблице (Табл.2.2)

Таблица 2.2. Таблица исходных данных примера 2.11.

	A	B	C	D	E	F	G
1	Начальное значение, Р	Количество периодов, n	Годовая процентная ставка, i	Количество начислений m1	Количество начислений m2	Количество начислений m4	Количество начислений m12
2	300 000	6	10%	1	2	4	12

Формулы и функции вводим в табл. 2.3 и 2.4.

Таблица 2.3. Шаблон решения примера 2.11.

	C	D	E	F	G
4	Решение:
5		Раз в году	Раз в полугодие	Раз в квартал	Раз в месяц
6	Будущее значение, БС (S)
7

Таблица 2.4. Формулы шаблона

Адрес ячейки	Формула
D6:G6	=БС($C$2/D2;$B$2*D2;;-$A$2) →
D7:G7	=$A$2*(1+$C$2/D2)^($B$2*D2) →

Так как значение S вычислено, рассчитаем значения n, P и i, используя функции Excel и собственные формулы (табл. 2.5):

Таблица 2.5. Формулы шаблона

	C	D
8	Количество периодов КПЕР(mn), D8:G8, D9:G9	=КПЕР($C$2/D2;; -$A$2) →
9		=LOG(D7/$A$2)/LOG(1+$C$2/D2) →
10	Начальное значение ПС (Р), D10:G10, D11:G11	=БС($C$2/D2;$B$2*D2;;D6) →
11		=D7/(1+$C$2/D2)^($B$2*D2) →
12	Годовая процентная ставка СТАВКА (i) , D12:G12, D13:G13	=D2*СТАВКА($B$2*D2;;- $A$2;D6) →
13		=D2*(D7/$A$2)^(1/($B$2*D2))-1) →

Пример 2.12. Ставка банка по срочным валютным депозитам составляет 13% годовых. Определить реальную доходность (т.е. эффективную ставку), если процентов выплачиваются: ежемесячно, ежеквартально, раз в полугодие, раз в год.

По рассчитанным значениям определить номинальные процентные ставки.

Решение. Разместим исходные данные в таблице (Табл.2.6)

Таблица 2.6. Таблица исходных данных примера 2.12

	A	B	C	D	E
1	Годовая процентная ставка, i	Количество начислений m1	Количество начислений m2	Количество начислений m4	Количество начислений m12
2	13%	1	2	4	12

Таблица 2.7.Шаблон решения примера 1.2

	C	D	E	F	G
4		Раз в году	Раз в полугодие	Раз в квартал	Раз в месяц
5	ЭФФЕКТ
6
7	НОМИНАЛ
8

Таблица 2.8. Формулы шаблона

ячейки	Формула	ячейки	Формула
B5:E5	=ЭФФЕКТ($A$2;B2) →	B7:E7	=НОМИНАЛ(B5;B2) →
B6:E6	=(1+$A$2/B2)^B2-1 →	B8:E8	=B2*((B5+1)^(1/B2)-1) →

Пример 2.13. Ставка банка по срочным валютным депозитам на начало года составляет 18% годовых, начисляемых раз в квартал. Первоначальная сумма вклада 2000 долл. В течение года ожидается снижение ставок раз в квартал на 1, 2, и 3% соответственно. Определить величину депозита к концу года

По рассчитанным значениям определить номинальные процентные ставки.

Решение. Формулы и функции для решения задачи вводим в табл.2.9.

Таблица 2.9. Таблица исходных данных примера 2.13

	A	B	C	D	E
1	Периоды начислений	I квартал	II квартал	III квартал	IV квартал
2	Начальная сумма	$2000
3	Годовая процентная ставка	18%
4	Снижение ставок	0%	1%	2%	3%
5	Количество начислений	4
6	БЗРАСПИС

В ячейки В6 и С6заносим формулы:

B6:{=БЗРАСПИС(B2;(B3-B4:E4)/B5)}

C6:{=ПРОИЗВЕД(B2;1+(B3-B4:E4)/B5)}

Фигурные скобки свидетельствуют, что данные формулы являются формулами массива. Для заполнения массива результатами расчетов, его выделяют, активизируют (открывают) формулу массива и одновременно нажимают клавиши Ctrl+Shift+Enter/ Фигурные скобки при вводе формулы массива набирать не надо, они появляются автоматически.

Задачи по вариантам

Задача 1. Сбербанк начисляет ежегодно 4% сложных. Если клиент положил на депозит 250 000 руб., то каковы суммы будут на его счету через 4 года и через пять лет и три месяца?

Задача 2. Сбербанк начисляет ежегодно 4% сложных. Если клиент положил на депозит 250 000 руб., то каковы суммы будут на его счету через 4 года при капитализации процентов раз в квартал и ежемесячно?

Задача 3. Ссуда размером 250 тысяч руб. выдана на 5 лет под 12% сложных годовых. Определить, во сколько раз изменится наращенная сумма, если ставку уменьшить на 2,5%.

Задача 4. По какой ставке сложных процентов годовых необходимо отдать в рост капитал, чтоб первоначальный капитал в размере 280 тыс. руб. за 190 дня увеличился в 1,1 раза.

Задача 5. Цена актива равняется 10 000 рублям. Его годовая доходность по ставке сложных процентов составила 11%. Определить, по какой цене был куплен актив.

Задача 6. Господин С. желает вложить деньги в банк под 6% годовых с ежемесячной капитализацией. Какую начальную сумму ему необходимо положить на счет, чтобы через пять с половиной лет получить 4 000 руб.?

Задача 7. Через 60 дней после подписания договора должник уплатит 4 000 000 руб. Кредит выдан на условиях 12% годовых (проценты сложные).

Какова первоначальная сумма займа. Рассчитать дисконт.

Задача 8. Три платежа S₁ =5 млн. руб., S₂ =1 млн. руб., S₃ =4 млн. руб. со сроками уплаты соответственно через 70, 120 и 140 дней заменяются одним сроком уплаты через 100 дней при сложной ставке 15% годовых. Найти сумму консолидированного платежа (год принять равным 360 дней).

Задача 9. Фирма, в погашение задолженности банку за предоставленный кредит под 10% годовых, должна произвести 2 платежа в сроки 2.05 (122-й день),20.08 (232-й день) суммами S₁ = 2млн. руб. и S₂ = 3 млн. руб. Фирма договорилась объединить оба платежа в один суммой S₀= 6 млн. руб. с продлением срока выплаты. Найти срок выплаты консолидированного платежа.

Задача 10. Вексель выдан на 10 000 руб. с уплатой 15 октября. Владелец погасил его 15 августа того же года по сложной процентной ставке 10% годовых. Какую сумму он получил.

Задача 11. Кредит предоставляется на срок 10 лет по ставке 5% сложных годовых. Заемщик хочет получить его под простые проценты ( сумма и срок погашения те же ). Какая ставка простых процентов должна быть указана в контракте ?

Задача 12. Финансовая компания дает ссуду 500 000 руб. на 4 года под сложный процент, равный 6% в год. Какую сумму получит клиент в момент получения ссуды?

Задача 13. Фирма берет в банке ссуду размером 600 000 руб. на 3 месяца под 9% сложного дисконта. Какую сумму она должна вернуть через три месяца?

Задача 14. Фирма обещалась заплатить за полученное от города помещение 1 200 т.руб. через 5 лет и еще 500 т.руб. через 8 лет относительно момента заключения договора. В силу сложившихся обстоятельств, фирма решила пересмотреть условия сделки: 700 т.руб. выплатить через 3 года, а остальной долг погасить через 6 лет. Какая сумма должна быть выплачена через 6 лет при условии начисления 8% сложных годовых.

Задача 15. Банк выплачивает по вкладам 10% сложных годовых. Какова должна быть доходность банковских операций при месячном, ежеквартальном и полугодовом начислении процентов?

Задача 16. Какая суммы предпочтительнее при ставке 7% сложных годовых: $1000 сегодня или $2000 через 8 лет?

Задача 17. Вдень рождения сына родители открыли на его имя счет в банке размером $2000 под 9% годовых. Какой будет эта сумма к двадцатилетию сына?

Задача 18. Какую ставку должен назначить банк, чтобы при годовой инфляции в 11%, реальная ставка оказалась 6%?

Задача 19. Вычислить эффективную процентную ставку, если банк начисляет проценты ежеквартально, исходя из номинальной процентной ставки 10% годовых.

Задача 20. Рассчитать, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку 10% годовых.

Задача21. По какой ставке сложных процентов годовых необходимо отдать в рост капитал, чтоб первоначальный капитал в размере 200 тыс. руб. за 256 дней увеличился в 1,5 раза.

Задача 22. Цена актива равняется 18 000 рублям. Его годовая доходность составила 15%. Определить, по какой цене был куплен актив.

Задача 23. Через 100 дней после подписания договора должник уплатит 1800 000 руб. Кредит выдан на условиях 11% годовых (проценты сложные). Какова первоначальная сумма займа? Рассчитать дисконт.

Задача 24. Через 150 дней предприятие должно получить по векселю 2 000 000 руб. Банк приобрел вексель с дисконтом. Банк учел вексель по учетной ставке 12% сложных годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

Задача 25. По договору зафиксирован платеж через 3 года в размере 1 000 тыс. руб. Через год процентная ставка увеличится. Кому это выгодно: кредитору или заемщику?

Задача 26. Фирма, в погашение задолженности банку за предоставленный кредит под 25% сложных годовых, должна произвести 2 платежа в сроки 2.05 (122-й день), 18.08 (230-й день) суммами S₁ = 4 млн. руб. и S₂ = 1 млн. руб. Фирма договорилась объединить оба платежа в один суммой S₀= 7 млн. руб. с продлением срока выплаты. Найти срок выплаты консолидированного платежа.

Задача 27. Две суммы,14 и 8 млн. руб., должны быть выплачены 23.08.13 (235) и 11.01.14 (11). Стороны договорились пересмотреть условия контракта: должник 6.12.13 (340) выплачивает 14 млн. руб., а остаток долга гасится 1.04.14 (91). Найти эту сумму при условии, что пересчет осуществляется по ставке сложных процентов, равной 12% (год равен 365 дней).

Задача 28. Финансовая компания дает ссуду 1 800 000 руб. на 2 года под сложный процент, равный 8% в год. Какую сумму получит клиент в момент получения ссуды?

Методические указания: при расчетах использовать схему сложного дисконта.

Задача 29. Фирма обещалась заплатить за полученное от арендодателя помещение 900 т.руб. сегодня и еще 1 000 т.руб. через 6 лет относительно момента заключения договора. В силу сложившихся обстоятельств, фирма решила пересмотреть условия сделки: 500 т.руб. выплатить через 2 года, а остальной долг погасить через 5 лет. Какая сумма должна быть выплачена через 5 лет при условии начисления 8% сложных годовых.

Задача 30. Транспортная компания собирается приобрести станок стоимостью 800 000 руб. У компании есть два варианта схемы финансирования: либо выплатить цену станка в течение 5 лет по 160 000 руб. в конце каждого года, либо в момент покупки заплатить 200 000 руб., а затем выплачивать в течение четырех лет по 150 000 руб. Выяснить, какой вариант выгоднее, при условии, что стоимость капитала составляет 12% сложных годовых.

Задача 31. Коммерческий банк принимает вклады от населения на следующих условиях:

1. С выплатой 12% годовых, начисляемых ежегодно;

2. С выплатой 11,5% годовых, начисляемых раз в полугодие.

Какой вид вклада вы предпочтете и почему ?

Задача 32. У Вас на счете в банке 150 000 руб. Банк платит 12% годовых. Вам предлагают удвоение капитала через 6 лет. Принимать ли это предложение ?

Задача 33. Вы имеете сумму 30 000 руб. и хотели бы удвоить эту сумму через 5 лет. Каково минимальное значение процентной ставки ?