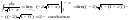- •2.Сформулируйте теорему Ролля.
- •Дайте определение интеграла с переменным верхним пределом. Докажите теорему Ньютона-Лейбница для определенного интервала.
- •5 Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •4. Дайте определение предела ф-ции двух переменных в точке. Имеет ли ф-ция предел в точке (0,0)?
- •1. Докажите ограниченность сходящейся последовательности.
- •2. Сформулируйте теорему Роля. В чем состоит ее геометрический смысл.
- •3. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •6. Найти производную функции f(X,y) в точке м по заданному направлению:
- •1. Дайте определение предела последовательности. Может ли последовательность иметь два предела? Ответ обоснуйте.
- •2. Дайте определение дифференциала ф-ции в точке. Используя дифференциал, найдите приближенное значение для: ln 1,05.
Билет 4
1)
Предел последовательности.
последовательности
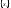 ,
если для любого положительного числа
,
если для любого положительного числа
 существует такой номер
существует такой номер
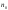 ,
начиная с которого все члены
последовательности отличаются от а
по модулю
меньше, чем на
,
начиная с которого все члены
последовательности отличаются от а
по модулю
меньше, чем на
 .
.

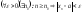 .
.
Предел
суммы двух сходящихся последовательностей
равен сумме пределов двух сходящихся
последовательностей. Если
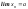 и
и
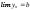 ,
то
,
то
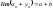
пр1
.

пр2.
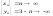 ,
,
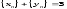
2 Дайте определение производной функции в точке.
 ,
где
,
где
 ,
а
,
а
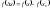
Геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x0)).
Да следует:
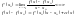

3) Функция y=f(x) ограниченная на отрезке [a,b] называется интегрируемой на этом отрезке, если существует единственное число I, разделяющее множество нижних и верхних сумм Дарбу для всевозможных разбиений отрезка [a,b]. Если функция y=f(x) интегрируема на отрезке [a,b], то единственное число разделяющее эти два множества, называется определенным интегралом функции y=f(x) на отрезке [a,b] и обозначается
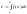
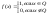
Как
бы ни разбили Т, в любом отрезке разбиения
 обязательно есть рациональные и
иррациональные точки, поэтому для
любого отрезка
обязательно есть рациональные и
иррациональные точки, поэтому для
любого отрезка
 и
и
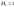 .
Тогда все нижние суммы Дарбу
.
Тогда все нижние суммы Дарбу
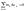 т.к.все
т.к.все
 и
все верхние Дарбу
и
все верхние Дарбу
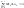 ,
т.к -
,
т.к -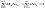 длина
отрезка [0,1] . Так множество нижних сумм
состоит их одного числа
длина
отрезка [0,1] . Так множество нижних сумм
состоит их одного числа
 и множество верхних сумм состоит их
одного числа
и множество верхних сумм состоит их
одного числа
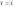 ,
так что любое число из отрезка разделяет
множество X
и Y.
Значит, функция не является интегрируемой
на отрезке [0,1]
,
так что любое число из отрезка разделяет
множество X
и Y.
Значит, функция не является интегрируемой
на отрезке [0,1]
4. Дайте определение однородной функции.Пусть D из Rn – область в Rn, содержащая с каждой своей точкой (x1, x2, …., xn) и все точки вида (tx1, tx2, …., txn) при t>0 функция f(x1, x2, …., xn) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx1, tx2, …., txn)=tλ f(x1, x2, …., xn).
Пример однородной функции степени 3:
F
(x,y)=x2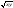
F (tx, ty)=t2x2√(tx*ty)=t3 F (x,y)
5. Необходимый признак сходимости. Если ряд сходится, то предел его общего члена равен нулю. Эквивалентная формулировка: Если предел общего члена ряда не равен нулю или не существует, то данный ряд расходится.
Доказательство.
Пусть данный ряд сходится и его сумма
равна S.
Для любого натурального n
имеем
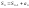 ,
или
,
или
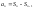 (*). При
(*). При
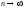 обе частичные суммы
обе частичные суммы
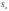 и
и
 стремятся к пределу S,
поэтому из равенства (*) следует, что
стремятся к пределу S,
поэтому из равенства (*) следует, что
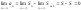 .
Мы установили только необходимое
условие сходимости ряда, т. е. условие,
при нарушении которого ряд не может
сходиться. С помощью этого признака
можно доказывать только расходимость
ряда.
.
Мы установили только необходимое
условие сходимости ряда, т. е. условие,
при нарушении которого ряд не может
сходиться. С помощью этого признака
можно доказывать только расходимость
ряда.
Пример:
 В этом случае предел общего члена ряда,
очевидно, равен нулю, однако ряд
расходится. Действительно, если бы
данный ряд сходился, то сходился бы и
ряд
В этом случае предел общего члена ряда,
очевидно, равен нулю, однако ряд
расходится. Действительно, если бы
данный ряд сходился, то сходился бы и
ряд
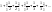 ,
полученный из данного ряда группировкой
членов. Но общий член последнего ряда
равен 1, и для него не выполнен необходимый
признак сходимости.
,
полученный из данного ряда группировкой
членов. Но общий член последнего ряда
равен 1, и для него не выполнен необходимый
признак сходимости.





Билет№5
1.Дайте определение бесконечно большой последовательности. Что означает запись “limn→∞xn=-∞”? Приведите пример двух бесконечно больших последовательностей, сумма которых является бесконечно малой последовательностью.
Последовательность {Un} называют бесконечно большой, если для любого, сколь угодно большого, числа А найдется такой номер N, что для всех членов последовательности, номера которых больше N, выполяется неравенство: | Un |>A.
Выражение limn→∞xn=-∞ означает, что бесконечно большая последовательность состоит из отрицательных членов.
Рассмотрим
две последовательности: {n}
и {-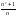 },
причем limn→∞n=+∞
и limn→∞-n=-∞.
},
причем limn→∞n=+∞
и limn→∞-n=-∞.
Тогда
образуется новая последовательность:
{n- }={-
}={-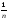 },
тогда limn→∞(-
},
тогда limn→∞(-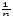 )=0,
причем последовательность {-
)=0,
причем последовательность {-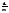 }
– б.м.
}
– б.м.
2.Сформулируйте теорему Ролля.
Теорема Ролля
Пусть
ф-ция
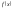 непрерывна на отрезке [a;b],
дифференцируема на интервале (a;b)
и
непрерывна на отрезке [a;b],
дифференцируема на интервале (a;b)
и
 ,
то найдётся хотя бы одна точка
,
то найдётся хотя бы одна точка
 ,
в которой
,
в которой
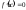 .
.

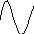
f(a)=f(b) найдется хотя бы 1 точка с, в которой касательная к кривой параллельна оси ОХ.
-
Дайте определение интеграла с переменным верхним пределом. Докажите теорему Ньютона-Лейбница для определенного интервала.
Для
функции y=f(x),
интегрируемой на отрезке [a;b],
интегралом с переменным верхним пределом
называется интеграл вида
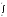 f(t)dt,
где
f(t)dt,
где

Пусть
функция y=f(x)
непрерывна на [a;b]
и F(x)
– первообразная для f(x),
тогда:
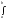 f(x)dx=F(b)-F(a)
f(x)dx=F(b)-F(a)
Доказательство:
Поскольку функция F(x) непрерывна на отрезке [a;b], то она интегрируема на этом отрезке и имеет первообразную на этом отрезке. Действительно, подставляя x=b, получим:
F(b)= f(t)dt,
а подставляя x=a,
получим: F(a)=
f(t)dt,
а подставляя x=a,
получим: F(a)=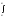 f(t)dt=0
Поэтому:
f(t)dt=0
Поэтому:
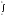 f(t)dt=F(b)-F(a)
Если F(x)
–другая первообразная для функции
f(x),
то выполняется равенство F(x)=Ф(x)+C
f(t)dt=F(b)-F(a)
Если F(x)
–другая первообразная для функции
f(x),
то выполняется равенство F(x)=Ф(x)+C
Имеем
F(b)-F(a)=(Ф(b)+C)-(Ф(a)+C)=Ф(b)-Ф(a)=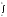 f(x)dx
f(x)dx
4.Дайте определение замкнутого множества в R2. Является ли множество D={(x,y) I 0<x≤3, 0<y≤6} замкнутым?
Множество Х называется замкнутым, если оно содержит все свои граничные точки, т.е. не являющиеся ни внутренними ни внешними для Х, то есть любая их окрестность содержит как точки, принадлежащие Х, так и точки не принадлежащие Х.
Не является, т.к. содержит не все свои граничные точки.
5 Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
Признак
Даламбера. Если
для ряда с положительными членами
 существует такое число q<1,
что при всех n
(или, начиная с некоторого n)
выполняется неравенство
существует такое число q<1,
что при всех n
(или, начиная с некоторого n)
выполняется неравенство
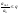 (*), то ряд сходится. Если же
(*), то ряд сходится. Если же
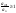 для всех или начиная с некоторого n,
то ряд расходится.
для всех или начиная с некоторого n,
то ряд расходится.
Доказательство.
Отбросив, если необходимо, несколько
первых членов ряда, можно считать, что
неравенство (*) выполняется для всех
п=1,
2, …Перепишем
это неравенство в виде
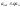 .
Отсюда имеем
.
Отсюда имеем
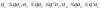 и т. д.; вообще, при любом п
справедливо
неравенство
и т. д.; вообще, при любом п
справедливо
неравенство
 .
Это показывает, что члены ряда
.
Это показывает, что члены ряда
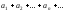 .
Не превосходят соответствующих членов
бесконечной геометрической прогрессии
.
Не превосходят соответствующих членов
бесконечной геометрической прогрессии
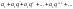 . Поскольку по условию
. Поскольку по условию
 <1,
эта прогрессия сходится. В силу первого
признака сравнения сходится и данный
ряд. В случае, когда
<1,
эта прогрессия сходится. В силу первого
признака сравнения сходится и данный
ряд. В случае, когда
 ,
имеем неравенство
,
имеем неравенство
 ,
т. е. члены ряда образуют неубывающую
последовательность, и поэтому не
выполняется необходимый признак
сходимости ряда, что доказывает теорему
полностью.
,
т. е. члены ряда образуют неубывающую
последовательность, и поэтому не
выполняется необходимый признак
сходимости ряда, что доказывает теорему
полностью.
6.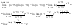
7.
8.
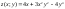 в
т. М(-2;1) по напр
в
т. М(-2;1) по напр
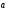 =(3;4)
=(3;4)
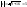 .
.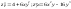
В
т.М(-2;1):

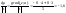
9.
Билет№6
№2 возрастающая последовательность
 ,
где
,
где
 ,
а
,
а
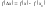
Геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x0)).
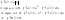
№3 первообразная

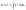
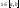 -
первообразная для
-
первообразная для

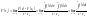
Применим теорему о среднем

где
промежуточная точка с находится между
x
и
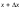 ,
поэтому
,
поэтому
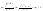
Т.к.
функция f(x)
непрерывна и
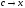 при
при
 то
то
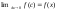 .
Функция f(x)
непрерывна на [a,b]
имеет на этом отрезке первообразную
.
Функция f(x)
непрерывна на [a,b]
имеет на этом отрезке первообразную .
.
№4Открытое множество
№5особое решение дифференциального уравнение

Особая – точка, в которой нарушается единственность задачи Коши.
Точки через которые не проходит ни одна интегральная кривая или проходит более одной интегральной кривой, называются особыми точками данного дифференциального уравнения . Может случиться , что некоторая интегральная кривая уравнения состоит из одних особых точек. Такая кривая называется особым решением уравнения
 ;
;
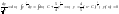
Через
ось ОХ проходит по крайней мере две
интегральные кривые
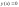 -особое
решение.
-особое
решение.




\
Билет 7
1
Число а
называется правым
(левым)
пределом функции в точке а, если для
любой сходящейся к а последовательности
x1,
x2,
x3,…,xn
такой, что xn<a
(xn>a)
соответствующая последовательность
 сходится
к А.
сходится
к А.

2
Пусть ф-ция
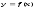 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
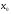 (∆
(∆ =
=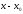 ).
Производной ф-ции
).
Производной ф-ции
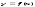 в точке
в точке
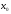 называется предел отношения
называется предел отношения
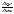 ,
когда
,
когда
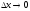 (при условии, что предел отношения
(при условии, что предел отношения
 существует). Обозначение
существует). Обозначение
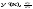 .
.
31) Решение.
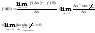
3 Несобственным интегралом ф-ции f(x) не ограниченной слева от т. b называется конечный предел определенного интеграла f(x) на [a;c2].
Обозн.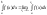 Если левый предел является конечным,
то говорят, что интеграл от неограниченной
функции слева от верхнего предела
сходится, а если нет, то расходится
(аналогично выводится от неограниченной
справа в т. а
Если левый предел является конечным,
то говорят, что интеграл от неограниченной
функции слева от верхнего предела
сходится, а если нет, то расходится
(аналогично выводится от неограниченной
справа в т. а
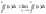
2)
Аналогично несобственному интегралу
с бесконечным верхним пределом (см. 85)
Так при
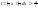
Поскольку
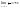 То
То
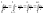 значит интеграл сходится при
значит интеграл сходится при
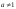
4 Если z=f(x;y) дифференцируема в точке (х0;y0), то в этой точке она непрерывна.
Пусть
ф-ция z=f(x;y)
дифференцируема в точке (х0;y0),
тогда справедливо
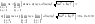
 ф-ция
z=f(x)
непрерывна в точке (х0;y0).
ф-ция
z=f(x)
непрерывна в точке (х0;y0).
5
Система
n-
функций
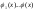 наз линейно зависимой на мн-ве X
, если хотя бы одна из них линейно
выражается через остальные, напр
наз линейно зависимой на мн-ве X
, если хотя бы одна из них линейно
выражается через остальные, напр
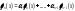 ,
,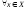
Если ни одна из них линейно н выр-ся через ост, то сист ф-ций наз. Линейно Независ

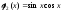
т.к.
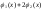
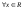
y1, y 2, …, yk.
c1
y1+c2
y
2+…+ ck
y
k=0
для любого х D.
D.
у=1, у=х, у=х2 на R
c1
1+c2
х+c3
х2=0
для любого х R
R
Продифференцируем дважды:
c2 +2c3 х=0
2c3=0
c1+c2 х+c3 х2=0 c1=0
c2
+2c3
х=0 c2=0
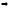 у=1, у=х, у=х2
– л.н.з.
у=1, у=х, у=х2
– л.н.з.
2c3=0 c3=0
6. Limx→∞x(31/4x-1)~limx→∞x·(1/4x)·ln3=(ln3)/4
7. ∫(16x+5)lnXdx =16∫xlnXdx+5∫lnXdx= 8∫lnXdx2+5xlnX-5∫xdlnX= 16xlnX-16∫x·(1/x)dx+5lnX-5x=
21lnX-21x.
8. z(x,y)=x2+y2-2lnX-27lnY, x>0, y>0
z´x=2x-2/x, z´y=2y-72/y
z´x=z´y=0, x=1, y=6
(1,6) – стационарная точка
z´´xx=2+2/x2, z´´yy=2+72/y2, z´´xy=0
2+2/x2 0
0 2+72/x2 >0 след. (1,6) – точка минимума
9. y´-2(y/x)=-x2
y´-2(y/x)=0
dy/dx=2y/x
dy/y=2dx/x
lnY=2lnX+2lnC=2lnCX
y=e2lnCX=CX2
y=C(x)·x2
y´=C´(x)x2+2x·C(x)
C´(x)x2+2x·C(x)- 2x·C(x)=-x2
C´(x)=-1, C(x)=-x+C
Y=-x3+Cx2
10.

Билет 9
1.определения
предела
Число
 называется пределом функции
называется пределом функции
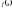 в точке
в точке
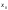 ,
если для любой сходящейся к
,
если для любой сходящейся к
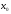 последовательности значений аргумента,
отличных от
последовательности значений аргумента,
отличных от
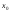 ,
соответствующая последовательность
значений функции сходится к числу
,
соответствующая последовательность
значений функции сходится к числу
 ,
т. е.
,
т. е.
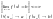

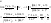
2.Теорема
о произведения двух функций
Если функции
 и
и
 дифференцируемы в точке
дифференцируемы в точке
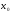 то произведение этих функций также
дифференцируемо и выполняется следующая
формула:
то произведение этих функций также
дифференцируемо и выполняется следующая
формула:
 .
.
Доказательство:
Пусть приращения функций
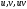 вычисляются только в точке
вычисляются только в точке
 ,
так что
,
так что
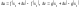

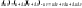
Из
дифференцируемости функций
 и
и
 в точке
в точке
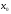 следует их непрерывность в
следует их непрерывность в
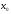 ,
поэтому
,
поэтому
 и
и
 ,
когда
,
когда
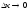 .
Следовательно,
.
Следовательно,
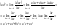
3.
Несобственный интеграл
Пусть функция y=f(x)
не ограничена на отрезке [a,b],но
интегрируема на любом меньшем отрезке ,
где
,
где
 .
Тогда если существует конечный предел
.
Тогда если существует конечный предел
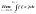 ,
то его принимают за несобственный
интеграл
,
то его принимают за несобственный
интеграл
 от неограниченной функции f(x):
от неограниченной функции f(x):
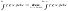
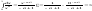 сходится
при
сходится
при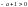 т.е при
т.е при
 .
.
4.
Лкальный экстремум Точка
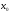 называется точкой локального максимума
(минимума) функции
называется точкой локального максимума
(минимума) функции
 ,
если для всех
,
если для всех
 и
и
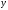 из
некоторой окрестности точки
из
некоторой окрестности точки
 выполняется неравенство:
выполняется неравенство:
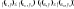
Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.
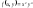
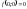 ,
,
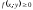 =>
=>
 - локальный минимум.
- локальный минимум.
5. Даламбер . Если существует предел
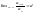 то
ряд сходится в случае d<1
и расходится в случае d>1
то
ряд сходится в случае d<1
и расходится в случае d>1
Доказательство:
Пусть d<1
Возьмем некоторое число q
между d
и 1 . Из условия
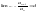 следует что начиная с некоторого номера
n,
будет выполняться неравенство
следует что начиная с некоторого номера
n,
будет выполняться неравенство
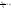 .
На основание теоремы(признак Даламбера)
отсюда следует сходимость ряда. Случай
d>1
разбирается аналогично . В Формулировке
этой теоремы ничего не говорится о
случае d=1.
При d=1
возможна как сходимость так и расходимость
ряда . Например гармонический ряд, для
которого d=1
расходится, а ряд
.
На основание теоремы(признак Даламбера)
отсюда следует сходимость ряда. Случай
d>1
разбирается аналогично . В Формулировке
этой теоремы ничего не говорится о
случае d=1.
При d=1
возможна как сходимость так и расходимость
ряда . Например гармонический ряд, для
которого d=1
расходится, а ряд
 для
которого также d=1
сходится.
для
которого также d=1
сходится.

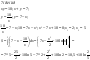

Билет 11
1.
Определение предела последовательностиЧисло
a
называют пределом последовательности
xn
 limn→∞xn=a,
если для любого положительного сколь
угодно малого числа ε>0
существует номер n0(ε)
такое, что начиная с этого номера все
члены последовательности xn
удовлетворяет неравенству 〡xn-a〡<ε.
limn→∞xn=a,
если для любого положительного сколь
угодно малого числа ε>0
существует номер n0(ε)
такое, что начиная с этого номера все
члены последовательности xn
удовлетворяет неравенству 〡xn-a〡<ε.
 limn→∞xn=a
⇒
для любого ε>0
limn→∞xn=a
⇒
для любого ε>0
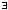 no(ε)∈N:
no(ε)∈N:
 n≥no
⇒〡xn-a〡<ε.
n≥no
⇒〡xn-a〡<ε.
.
Пусть
 .
Положим
.
Положим
 и найдем номер
и найдем номер
 ,
начиная с которого
,
начиная с которого
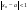 для
для
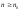 .
Отсюда следует
.
Отсюда следует
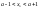 для всех
для всех
 .
Заменим отрезок
.
Заменим отрезок
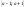 таким отрезком
таким отрезком
 ,
чтобы в него попали не только числа
,
чтобы в него попали не только числа
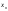 ,
,
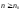 ,
но и все числа
,
но и все числа
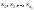 .
Тогда будем иметь
.
Тогда будем иметь
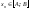 для всех
для всех
 ,
что означает ограниченность множества
,
что означает ограниченность множества
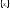
2.Локальный
экстремум Точка
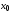 называется точкой локального max
[min]
ф-ции
называется точкой локального max
[min]
ф-ции
 ,
если для всех
,
если для всех
 из некоторой окрестности точки
из некоторой окрестности точки
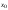 выполняется неравенство
выполняется неравенство
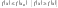
y
max
Локальный max
и min
объединяются общим названием локальный


экстремум.
x
 x0
x0


Для
того, чтобы дифференцируемая ф-ция
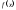 имела в точке
имела в точке
 локальный экстремум необходимо, чтобы
в этой точке выполнялось равенство
локальный экстремум необходимо, чтобы
в этой точке выполнялось равенство
 .
.
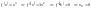 +
0 +
+
0 +
 но
но
 =0
не является точкой экстремума.
=0
не является точкой экстремума.
3.
Формула Ньютона-лейбница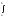 f(x)dx=
F(b)-F(a),
где F(x)-любая
первообразная для f(x)
на [a;b].
f(x)dx=
F(b)-F(a),
где F(x)-любая
первообразная для f(x)
на [a;b].
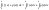
Доказательство:
Из
свойств неопределенного интеграла
следует, что если F1(x)–первообразная
для функции f1(x)
, а F2(x)–
первообразная для функции f2(x),
то первообразная для суммы функций
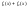 будет
служить сумма первообразных
будет
служить сумма первообразных

Следовательно

5.
Уравнение Коши для уравненияПусть
 -нормальная
форма уравнения 2 порядка. Найти решение
этого уравнения, удовлетворяющее
начальным условиям
-нормальная
форма уравнения 2 порядка. Найти решение
этого уравнения, удовлетворяющее
начальным условиям
 ,
,
 при
при
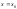 ,
,
 ,
, пример:
пример: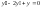





Билет 12
1)Непрерывная
в точке. Функция
 ,
определенная в некоторой окрестности
точки
,
определенная в некоторой окрестности
точки
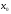 ,
называется непрерывной в этой точке,
если предел функции в точке
,
называется непрерывной в этой точке,
если предел функции в точке
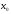 существует и равен значению в этой
точке:
существует и равен значению в этой
точке:
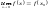
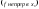
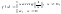
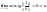 .
При
.
При
 - функция непрерывна.
- функция непрерывна.
2
)Производной
функции в точке![]() в точке
в точке
![]() называется предел отношения приращения
функции в этой точке к приращению
аргумента при
называется предел отношения приращения
функции в этой точке к приращению
аргумента при
![]() (если этот предел существует).
(если этот предел существует).
Для
обозначения производной функции
![]() применяются следующие символы
применяются следующие символы
![]()
![]() )
или
)
или
![]() :
:
![]() .
.
Четная всегда симметрична относительно оси ох поэтому до 0 производная идет в одном направлении, а после нуля точно также, но с другим знаком
f(x)=x4, xо-произвольное число
f
′(xо)=

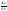 =
=
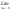
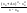 =
=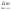
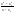 =4
=4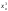
3)Несобственный
интеграл Пусть функция y=f(x)
интегрируема на каждом конечном отрезке
[a,b],
т.е. существует определенный интеграл
 .
Тогда за несобственный интеграл
.
Тогда за несобственный интеграл
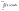 принимают
предел функции
принимают
предел функции
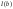 ,
когда b
стремится к бесконечности
,
когда b
стремится к бесконечности

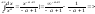 сходится
при
сходится
при
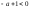 ,
,
 .
.
5) Определение: уравнение второго порядка вида: у,,+р(х)у,+q(х)у=f(x) , где у - искомая функция, р(х), q(х) и f(x) – непрерывные функции на некотором интервале (a, b), называется линейным дифференциальным уравнением второго порядка.
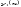 и
и
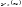 - решения дифура.
- решения дифура.
 -
решения однородного дифура.
-
решения однородного дифура.
Тогда
 .
.




Билет 15
1.Последовательность
{xn}
бесконечно малой, если limx→∞xn=0,
т.е. {xn}
– бесконечно малая, если
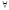 ε>0
ε>0
 no:
no:
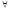 n>n0
⇒
〡xn〡<ε.
n>n0
⇒
〡xn〡<ε.
произведение бесконечно малой и ограниченной последовательности является бесконечно малой последовательностью.
Sinn*1\x=0
2.)Производной
функции
![]() в точке
в точке
![]() называется предел отношения приращения
функции в этой точке к приращению
аргумента при
называется предел отношения приращения
функции в этой точке к приращению
аргумента при
![]() (если этот предел существует).
(если этот предел существует).
Для
обозначения производной функции
![]() применяются следующие символы
применяются следующие символы
![]()
![]() )
или
)
или
![]() :
:
![]() .
.
f(x)=sinx, xо-произвольное число
f
′(xо)=
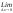
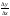 =
=
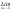
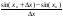 =
=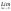
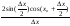 =
=
3. Функция F(x) называется первообразной функции y=f(x) на промежутке X, если F’(x)=f(x) для любого x∈X.
Совокупность всех первообразных для функции f(x) на X называется неопределенным интегралом этой функции.
. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
(∫f(x)dx)’=f(x)
(∫f(x)dx)’=(F(x)+C)=f(x)
d∫f(x)dx=(∫f(x)dx)’dx=f(x)dx
4.Как связаны производные по направлению и градиенты
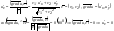


Билет 8
1.
Число а
называется пределом последовательности
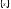 ,
если для любого положительного числа
,
если для любого положительного числа
 существует такой номер
существует такой номер
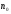 ,
начиная с которого все члены
последовательности отличаются от а
по модулю
меньше, чем на
,
начиная с которого все члены
последовательности отличаются от а
по модулю
меньше, чем на
 .
.

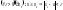 .
.
а)

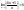 (у каждого должен быть свой пример)
(у каждого должен быть свой пример)
б)
 ;
;
2.
Эластичностью функции
 в точке
в точке
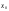 называется следующий предел
называется следующий предел
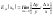 .
.
Эластичность
 - это коэффициент пропорциональности
между относительными изменениями
величин y
и x.
- это коэффициент пропорциональности
между относительными изменениями
величин y
и x.
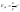
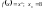
1.

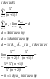
2.

3.

3.
Несобственный интеграл
Пусть
функция y=f(x)
интегрируема на каждом конечном отрезке
[a,b],
т.е. существует определенный интеграл
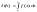 .
Тогда за несобственный интеграл
.
Тогда за несобственный интеграл
 принимают
предел функции
принимают
предел функции
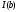 ,
когда b
стремится к бесконечности
,
когда b
стремится к бесконечности