Лабораторная работа № 5 Исследование параметров трехфазной цепи с нагрузкой, включенной по схеме звезда

Цель работы:

Исследовать трехфазную цепь с нагрузкой, включенной по схеме звезда

и установить взаимосвязь между линейными и фазными параметрами цепи.

Задание:

Измерить параметры и по опытным данным построить векторные диаграммы напряжений и токов для трехфазной цепи с нагрузкой, включенной по схеме звезда.

Установить роль нейтрального провода и влияние обрыва нейтрального и/или линейного провода на работу трехфазной цепи с нагрузкой.

Используемые приборы:

1. Стенд для исследования принципа работы и параметров 3-хфазной цепи,

состоящий из трехфазного трансформатора и нагрузок в виде ламп накаливания.

2. Амперметр переменного тока (мультиметр) с пределом измер. 0 – 5 А (4 шт.).

3. Вольтметр переменного тока (мультиметр) с пределом измер. 0 – 50 В (4 шт.).

Краткие теоретические сведения

Совокупность трех линейных цепей, в которых действуют синусоидальные источники ЭДС одинаковой частоты, отличающиеся по фазе одна от другой на величину угла φ = 2π/3 = 120⁰, называется трехфазной системой (цепью).

Такая цепь содержит генератор трехфазной системы ЭДС, линии передачи, потребители (нагрузки), например, электродвигатели, нагреватели, лампы и др.

Трехфазный генератор состоит из ротора (вращающегося индуктора, на валу которого закреплены постоянные магниты) и статора (внешней - не вращающейся части, на которой размещаются три фазные обмотки).

Обмотки фаз располагают на статоре таким образом, чтобы их магнитные оси были сдвинуты относительно друг друга на величину угла φ = 2π/3.

При вращении ротора генератора с угловой частотой ω, вокруг него возникает вращающееся магнитное поле, возбуждающее в фазных обмотках статора ЭДС индукции е_А, е_В и е_С одинаковой амплитуды U_m и частоты ω, но сдвинутые по фазе относительно друг друга на угол φ = 2π/3 = 120⁰ (рис. 5.1).

Трехфазную систему ЭДС с нагрузкой отображают графически (рис. 5.1), векторами, функциями комплексного переменного или тригонометрическими функциями. Представленная на рис. 5.1 трехфазная система питания (в тригонометрической форме в прямой последовательности) имеет следующий вид:

е_А = Е_m∙sin ωt; е_B = Е_m∙sin(ωt –2π/3); е_C = Е_m∙sin(ωt+2π/3). (5.1)

Угол сдвига фазы А принят равным нулю (φ_А=0); фазы В и С сдвинуты на 120^о.

Пример комплексной формы записи для описания параметров источника ЭДС:

Ē_А = Е; Ē_B = Е_B∙e_хр ^{– j2π/3}; Ē_C = Е_C∙e_хр^{– j4π/3} = Е_C∙e_хр ^j2π/3. (5.2)

где е_А – е_B – е_C – мгновенные значения источников ЭДС;

Ē_А, Ē_B, Ē_С – комплексы действующих значений ЭДС;

Е – действующее значение ЭДС. Е = Е_m/√2.

Соединение 3-х фазного источника с нагрузкой по схеме звезда

Соединение называют звездой, если три независимые цепи объединены таким образом, что концы фазных обмоток генератора и фазы приемников образуют два узла n и N (рис. 5.2). Провод, соединяющий узлы n-N называется нейтральным.

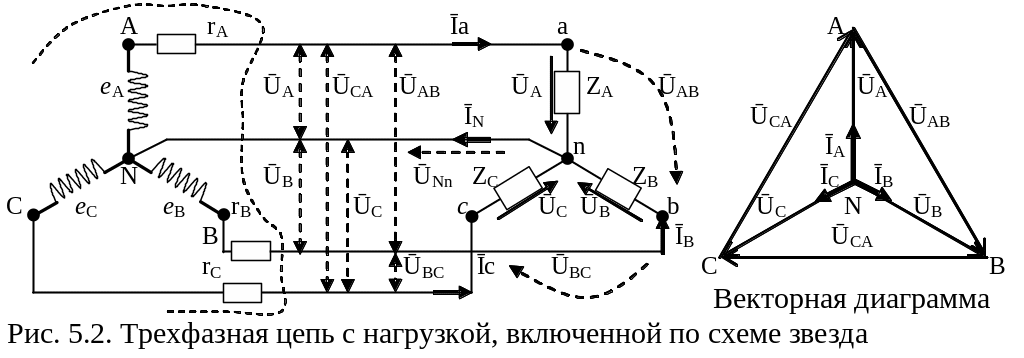
Напряжение U_А, U_В, U_С между началом и концом одноименной фазы (или между линейным и нейтральным проводом) называют фазным.

Напряжения U_АВ,U_ВС,U_СА между фазными проводами называют линейными.

Для симметричной системы питания справедливы соотношения:

е_А + е_В + е_С = 0; Ē_А + Ē_B + Ē_С = 0; Ū_А + Ū_B + Ū_С = 0. (5.3)

В тригонометрической форме фазные напряжения в нагрузке составят:

Ū_А =U_А∙cosφ+jU_А∙sinφ; Ū_В =U_В∙cosφ+jU_В∙sinφ; Ū_С =U_С∙cosφ+jU_С∙sinφ. (5.5)

(Sin ± 60⁰ = ± 120⁰ = ± /2 = ± 0,866; Cos ± 60⁰ = 0,5; Cos ± 120⁰ = – 0,5.

Н апример: Ū_А + Ū_B + Ū_С = [220]+[220·(-0,5)+j220·(–0,866)]+[220·(-0,5)+j220V·0,866] = 0.

В комплексной форме фазные напряжения можно записать в виде:

Ū_А = U_А∙e_хр ^jφa; Ū_B = U_B∙e_хр ^jφb; Ū_C = U_C∙e_хр ^jφc. (5.4)

В показательной форме, с учетом угла сдвига фаз между напряжениями:

Ū_А = U_А∙e_хр ^j0’; Ū_B = U_B∙e_хр^–j120’; Ū_C = U_C∙e_хр ^j120’. (5.6)

В схеме звезда с симметричной нагрузкой между линейными и фазными напряжениями существует зависимость: U_Л = U_Ф√3; (5.7)

Линейные напряжения связаны с фазными напряжениями соотношениями:

Ū_АВ = Ū_А–Ū_В; Ū_ВС = Ū_В–Ū_С; Ū_СА = Ū_С–Ū_А. [Ū_АВ+Ū_АВ+Ū_АВ = 0] (5.8)

Ū _АB = Ū_A – Ū_B = (220)–(–110 – j190,5) = (330+j190,5). (tg ⁺0,577 = +30⁰)

Ū _BC = Ū_B – Ū_C = (–110–j190,5)–(–110+j190,5)=(–j381). (tg = 90⁰)

Ū_CA = Ū_C – Ū_A = (–110+j190,5) – 220 = (–330+j190,5). (tg ^–0,577= –30⁰)

Нагрузки (приемники энергии) называются симметричными, если комплексные сопротивления Ź их фаз равны между собой:

Ź_А = Z_А∙e_хр ^jφa; Ź_B = Z_B∙e_хр ^jφb; Ź_C = Z_C∙e_хр ^jφc. (5.9)

т.е. равны полные сопротивления отдельных фаз: Ź_А = Ź_В = Ź_С = Ź_Ф

и одинаковы углы сдвига между фазами: φ_А = φ_В = φ_С = φ = 120^о.

Токи I_A, I_В, I_С в линейных проводах, называются линейными, а токи в обмотках генератора и в фазах приемника, называются фазными.

Между линейными и фазными токами существует зависимость: I_Л = I_Ф.

Ток в каждой фазе можно найти по закону Ома I_Ф = U_Ф/Z_Ф.

В тригонометрической форме токи в трехфазной цепи записывают в виде:

Ī_А = I_А∙cosφ+jI_А∙sinφ; Ī_В = I_В∙cosφ+jI_В∙sinφ; Ī_С = I_С∙cosφ+jI_С∙sinφ. (5.10)

В комплексной форме токи Ī можно записать в виде:

Ī_А = I_А∙e_хр ^jφa; Ī_B = I_B∙e_хр ^jφb; Ī_C = I_C∙e_хр ^jφc., (5.11)

В показательной форме, в случае симметричной нагрузки, эти токи составят:

Ī_А = I_А∙e_хр ^j0’; Ī_B = I_B∙e_хр^-j120’; Ī_C = I_C∙e_хр ^j120’. (5.12)

Применив к цепи закон Ома, а к узлу ‘n’ первый закон Кирхгофа, получим:

Ī_N = Ū_n/Ź_n = Ý_n∙Ū_n. i_N = i_А + i_В + i_С = 0 или Ī _N = Ī_А + Ī_В + Ī_С. (5.13)

При симметричной нагрузке ток Ī _N в нейтральном проводе отсутствует.

Это позволяет выполнить трехфазную сеть – 3-х проводной (без провода N-n).

Форма записи тока в нулевом проводе в тригонометрической форме имеет вид:

Ī _N = (I_А∙cosφ+jI_А∙sinφ) + (I_В∙cosφ+jI_В∙sinφ) + (I_С∙cosφ+jI_С∙sinφ). (5.14)

При несимметричной нагрузке расчет цепи производят методом узловых напряжений, определяя Ū_Nn между нейтралями источника ЭДС и нагрузки.

Ū _n = Ū_Nn = [Ý_a∙Ē_А +Ý_b∙Ē_B+Ý_c∙Ē_C] / (Ý_a +Ý_b +Ý_c +Ý_N). (5.15)

где Ý_a=(1/Ź_a), Ý_b=(1/Ź_b), Ý_c=(1/Ź_c), Ý_N =(1/Ź_N)

– комплексные проводимости.

По известным напряжениям источника Ū_А, Ū_В, Ū_С можно построить векторы фазных напряжений на нагрузке Ū_а, Ū_b, Ū_c (рис. 5.3). Комплексные значения напряжений в нагрузке находят из соотношений:

Ū_а = Ū_А –Ū_n , Ū_b = Ū_B –Ū_n , Ū_c = Ū_C –Ū_n. (5.16)

Из выр. (5.15) проводимость Y_N = 0 при обрыве нейтрального провода N-n.

Если сопротивление нейтрального провода Z_Nn = 0, то U_Nn = 0, но равенство U_Nn = 0 справедливо только в трехфазной цепи с симметричной нагрузкой.

В симметричной цепи при малом значении r_Линии фазные напряжения на нагрузках равны фазным напряжениям генератора: Ū_а = Ū_А. Ū_b = Ū_B. Ū_c = Ū_C.

Зная напряжения на фазах нагрузки, можно определить фазные токи:

Ī_A = Ī_a = Ū_a/Ź_a =Ý_a∙Ū_a; Ī_B = Ī_b = Ū_b/Ź_b =Ý_b∙Ū_b; Ī_C = Ī_c = Ū_c/Ź_c =Ý_c∙Ū_c. (5.17)

Токи в фазах приемника составят: Ī_a = Ū_a/Ź_a; Ī_b = Ū_b/Ź_b; Ī_c = Ū_c/Ź_c.

Сдвиг фаз между током и напряжением в нагрузке зависит от вида нагрузки.

Например, в цепи с реактивной нагрузкой аргумент составит: φ = arctg (X_Ф/R_Ф).

П ример: В симметричной 3-х проводной сети по схеме звезда с напряжением

U_Ф = 25(В) в каждой фазе включены нагрузки: R = 5,2; Х_L = 3 (Ом).

1) Определить в комплексной форме сопротивление и ток в цепи:

Ź = 5,2 - j3; Ź = √5,2² +(3²)∙e_xp ^{jarctg 3/5,2} = 6∙e_xp^j30° (Ом).

При симметричной нагрузке: Ź = Z_A∙e_хр ^j30° = Z_В∙e_хр ^j30° = Z_С∙e_хр ^j30° (Ом).

2) Используя свойство: Ū_А = U_А∙e_хр ^j0°; Ū_B = U_B∙e_хр^-j120°; Ū_C = U_C∙e_хр ^j120° (В)

определим ток в каждой фазе по закону Ома Ī = Ū/ Ź (A);

Ī_a = Ū_a/Ź_a = U_А∙e_хр ^j0’ / Z_A∙e_хр ^j30’ = U_А∙e_хр ^j0° / 6∙e_xp^j30° = 4,8∙e_хр^–j30’ (A);

Ī_b = Ū_b/Ź_b = U_B∙e_хр^–j120’/ Z_B∙e_хр ^j30’ = U_В∙e_хр ^–j120°/6∙e_xp^j30° = 4,8∙e_хр^–j150’(A);

Ī_с = Ū_c/Ź_c = U_C∙e_хр ^j120’/ Z_C∙e_хр ^j30’ = U_С∙e_хр ^j120° / 6∙e_xp^j30° = 4,8∙e_хр ^j90’(A).

-----------------------------------------------------------------------------------------------------------------------------

Активная и полная мощность в 3-х-фазной цепи с нагрузкой составит:

P_Ф = U_Ф∙I = I²∙R_Ф = U²_Ф/R_Ф; S_И = E_И∙I′; S_Н = U_НФ∙I_Ф′ = I²∙Z_Ф = U²_Ф/Z_Ф; (5.18)

Для симметричной нагрузки по схеме звезда суммарная мощность составит:

S = U_Л∙I′_Л∙√3 или S = 3∙U_Ф∙I′_Ф. (5.19)

При определении S = U·I′ необходимо записывать ток в сопряженной форме (I′)!

Суммарную мощность в трехфазной цепи с нагрузкой по схеме звезда вычисляют из условия баланса мощностей:

∑Р_И = ∑Р_Н. ∑P = P_A+P_B+P_C. ∑S_И = ∑S_Н. ∑S = S_A+S_B+S_C. (5.20)

В комплексной форме полная мощность в нагрузке имеет вид:

Ś = P+jQ; ∑Ś = Ś_A+Ś_B+Ś_C;

при этом ток записывают в сопряженной форме Ś = Ū∙Ī′. (5.21)

В 3-х проводной цепи при отключении одной фазы - нагрузки двух других фаз окажутся соединенными последовательно и будут под линейным напряжением.

В 4-х проводной цепи отключение одной фазы не приводит к изменению фазных напряжений других приемников независимо от их сопротивлений.

При коротком замыкании (КЗ) одной фазы в 3-х проводной цепи приемники двух других фаз окажутся под линейным напряжением. При КЗ фазная обмотка генератора (или питающего трансформатора) будет перегружена и выйдет из строя.

Методика построения векторных диаграмм для 3-х фазной цепи

с нагрузкой, включенной по схеме звезда)

Векторные диаграммы строят в масштабе напряжений m_U и токов m_I.

Векторная диаграмма напряжений на нагрузке строится совмещенной с векторной диаграммой напряжений источников ЭДС.

Линейные и фазные напряжения источников ЭДС неизменны, следовательно, линейные напряжения на нагрузках также неизменны и равны линейным напряжениям ЭДС, при условии, что сопротивлением проводов можно пренебречь:

Ū_ab = Ū_АВ. Ū_bс = Ū_ВС. Ū_са = Ū_СА.

Исключение составляют случаи обрыва линейных проводов.

Если Ū_АВ = Ū_ВС = Ū_СА, то при построении получим равносторонний треугольник линейных напряжений генератора. Нейтральная точка N генератора всегда находится в центре треугольника; фазные напряжения Ū_А, Ū_В, Ū_С сдвинуты относительно друг друга на 120⁰ (можно построить с помощью циркуля).

При наличии нейтрального провода с сопротивлением Z_N = 0 и при любой нагрузке U_Nn = 0, т.е. потенциалы нейтральных точек нагрузки n и N генератора совпадают. При отсутствии провода N-n и при несимметричной нагрузке появляется напряжение U_Nn между нейтральными точками. В этом случае из точек А, В, С проводят дуги радиусом U_a, U_b, U_c. Общая точка пересечения дуг N-n определяет потенциал между нейтральной точкой нагрузки и генератора.

Векторную диаграмму токов в нагрузке строят совмещенной с векторной диаграммой напряжений. Для каждой фазы нагрузки определяют угол сдвига фаз φ_Ф = φ_u–φ_i между напряжением и током в зависимости от вида нагрузки (рис. 6.2).

О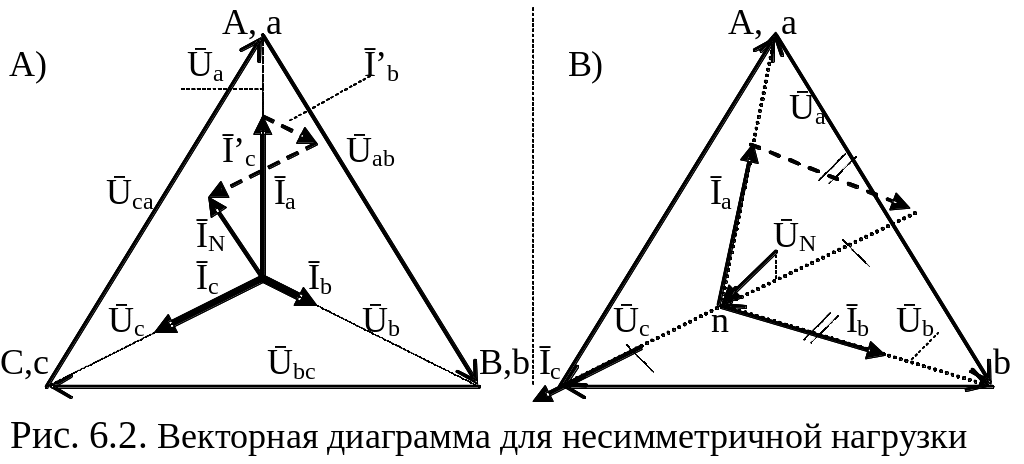 ткладывая на диаграмме фазных напряжений наг-рузок под соответству-ющими углами фазные токи, получают векторную диаграмму токов.

Т ок в нейтральном про-воде можно определить графическим суммирова-нием токов: Ī_n = Ī_a+Ī_b+Ī_c.

На рис. 6.2,а показана векторная диаграмма напряжений и токов неравномерной нагрузки, включенной по схеме звезда с нейтральным проводом. Отсутствие нейтрального провода нарушает симметрию фазных напряжений нагрузки, приводя к смещению между Ū_Nn источника и нагрузки (рис. 6.2,б). При обрыве одного из проводов, например, В-b в 4-х-проводной цепи, нагрузки данной фазы остаются без энергии: Ū_bn = 0 (рис. 6.3,а).

Режим работы двух других фаз не нарушается. Линейные напряжения Ū_ab, Ū_bc между оборванными и другими проводами уменьшаются до фазных величин.

Ток в нейтральном проводе определяется только двумя фазными токами.

Если дополнительно отключить также нейтральный провод, нагрузки двух других фаз оказываются включенными последовательно на линейное напряжение источника. Ток в фазах будет одинаков, а фазные напряжения на них пропорциональны их полным сопротивлениям (рис. 6.3,б).

Векторные диаграммы напряжений и токов можно строить либо по приведенной выше методике, либо используя известные программы: Mat_Cad, Exel, ACAD, Compas и аналогичные.

Порядок выполнения работы для цепи с нагрузкой по схеме звезда

1. Ознакомиться с электрической трехфазной цепью (схемой) стенда.

Активной нагрузкой 3-х фазной цепи могут служить лампы накаливания с нелинейной ВАХ и рабочими параметрами U_Н ≤ 40 В и P_Н ≤ 60 Вт. Поэтому, необходимо исследовать зависимость R_Н = (U_Н, I_Н) сопротивления лампы, измерив ток I_Н при напряжении U_Н = 3÷30 В с шагом U= 3 В (смотрите ЛР №1-дополнение).

2. Измерить токи I_Л, I_Ф и I_N и напряжения U_Л, U_Ф и U_N в цепи схемы.

* Тумблером S_N можно подключить или отключить нулевой провод.

3. Выполнить 3 опыта с симметричной или несимметричной нагрузкой.

А) Условие симметричной нагрузки; провод N включен / отключен.

Провести измерения параметров 3-х фазной цепи.

Б) Условие несимметричной нагрузки; провод N включен / отключен.

Повторить измерения линейных и фазных напряжений и токов

В) Отключить один из фазных проводов при отключенном / включенном нулевом проводе и провести измерения параметров 3-х фазной цепи.

Показания приборов для проведенных опытов записать в таблицу № 5.1.

4. Вычислить параметры цепи: сопротивления фазных нагрузок Z_Ф с учетом их свойств; мощности источников S_И и нагрузок Р_Н; мощности потерь Р_П в сопротивлениях источников и линиях передачи.

5. Проверить свойство отношений линейных напряжений к фазным U_Л/U_Ф.

6. В случае использования реактивных нагрузок в 3-х-фазной цепи, необходимо по измеренным данным доопределить параметры: Х (Ом); Q (ВАР); Cos φ

7. Построить векторные диаграммы линейных и фазных напряжений и токов для источников ЭДС и нагрузок с учетом фазового сдвига.

8. Оформить отчет, выполнив вычисления и записав выводы по работе.

Таблица № 5.1. Опыты с нагрузкой, включенной по схеме звезда (Y)

И змерено

Вычислено

C

nR

UЛ (B)

UФ (B)

U0 // I0

IЛ (A)

IФ (A)

*Л /*Ф

ZН(Ом)

rИ (Ом)

SИ (ВA)

РН (Вт)

РП (Вт)

1

Нагрузки симметричные

A

B

C

2

Нагрузки несимметричные

A

B

C

3

Линейный или фазный провод в обрыве

A

B

C

Если в 3-х-фазной цепи используются реактивные нагрузки, то для определения их параметров можно воспользоваться расчетной частью из ЛР № 3.

Контрольные вопросы:

1. Сформулировать основные положения и свойства 3-х-фазной цепи.

2. Каковы назначения и параметры 3-х фазной цепи?

3. Различия между фазными и линейными параметрами цепи.

4. Когда возможно использование несимметричной нагрузки?

5. Почему в нулевом проводе не ставят предохранитель?

6. К чему приводит обрыв нулевого провода?

7. К чему приводит отключение фазной нагрузки?

8. К чему приводит обрыв фазного провода?

9. К чему приводит замыкание между фазными проводами?

10. Записать формулу суммарной мощности 3-х фазной цепи с нагрузкой по схеме звезда и треугольник, используя только линейные и фазные напряжения и токи.

Литература

1. Касаткин А.С., Немцов М.В. Электротехника. – М.: Высш. шк., 2003. – 540 с.

2. Рекус Г.Г., Чесноков В.Н. Лабораторный практикум по электротехнике и основам электроники: Учебное пособие. – М.: Высш. шк., 2001. – 255 с.

3. Рекус Г.Г. Основы электротехники и промышленной электроники в примерах и задачах с решениями: Учебное пособие. – М.: Высш. шк., 2008. – 343 c.