Лабораторная работа № 2 Исследование линейной разветвленной электрической цепи с несколькими источниками постоянной эдс

Цель работы:

Определить параметры разветвленной цепи экспериментально и теоретически

Задание:

1. Измерить экспериментально параметры разветвленной электрической цепи.

2. Рассчитать теоретически параметры цепи по законам Ома и Кирхгофа

3. Построить потенциальную диаграмму для выбранного контура цепи.

Краткие теоретические сведения

Способ оценки параметров цепи на основе законов Ома и Кирхгофа

Используя законы Ома и Кирхгофа необходимо определить значения токов I₁ ÷ I₆, в электрической схеме (рис. 2.1) .

Согласно 1-го закона Кирхгофа - сумма токов в узле равна нулю, т.е. в узле электрической цепи заряд накапливаться не может.

I_К = 0. (2.1)

I₁ – I₃ – I₅ = 0 (для узла А);

I₅+ I₆ – I₄ = 0 (для узла В);

I₂ + I₃ – I₆ = 0 (для узла С).

*(В данном примере ключ S₁ замкнут).

По 1-му закону Кирхгофа для схемы с числом узлов n_У составляют (n_У – 1) уравнений. Токи, входящие в узел, можно записать со знаком “+”, а выходящие из узла токи - записать со знаком “–”.

Согласно 2-го закона Кирхгофа - сумма источников ЭДС в контуре равна сумме падений напряжений на элементах контура, т.е. в любом контуре электрической цепи соблюдается закон сохранения энергии.

m n n m n

Е_К = U_К = I_КR_{К ,} либо Е_К – I_КR_К = 0. (2.2)

k=1 k=1 k=1 k=1 k=1

В уравнении (2.2) ЭДС записывают со знаком (+) если действие ЭДС совпадает с направлением обхода контура, и со знаком (–), если не совпадает.

Для записи уравнений выбирают направление обхода контура (например, по часовой стрелке). По закону Ома падение напряжения на резисторе:

I_КR_К = U_Rк. (2.3)

записывают со знаком (–), если направление тока I в ветви совпадает с направлением обхода контура. Число уравнений, составляемых по 2-му закону Кирхгофа, равно числу n_К независимых контуров в цепи.

n_К = n_В – (n_У – 1), n_К = 6 – (4 – 1) = 3; (здесь ключ S₁ замкнут) (2.4)

где n_В – число ветвей; n_У – число узлов.

Независимым называют контур электрической цепи, который содержит хотя бы одну ветвь, не входящую в другие контуры.

Для цепи (рис. 2.1) с тремя независимыми контурами уравнения имеют вид:

E ₁ – E₄ – r₁I₁ – R₅I₅ – R₄I₄ = 0 или r₁I₁ + R₅I₅ + R₄I₄ = E₁ – E₄.

E₂ – E₄ – r₂I₂ – R₄I₄ – R₆I₆ = 0 или r₂I₂ + R₄I₄ + R₆I₆ = E₂ – E₄.

E₃ – R₃I₃ – R₆I₆ + R₅I₅ = 0. или R₃I₃ + R₆I₆ – R₅I₅ = E₃ . (2.5)

По законам Кирхгофа (для рис. 2.1) получают систему из 6-ти уравнений.

В результате решения системы уравнений находят искомые токи: I₁ ÷ I₆.

Для проверки результатов используют уравнение баланса мощностей:

Р_И = Р_Н . Е_К·I_К = I²_К·R_К, (2.6)

алгебраическая сумма мощностей всех источников в цепи равна алгебраической сумме мощностей, потребляемых нагрузками (приёмниками энергии).

Мощность источника в уравнении берут со знаком "+", если направление тока источника (I_И) совпадает с направлением действия ЭДС (Е).

При встречном направлении ЭДС и тока мощность считают отрицательной.

Пример определения разности потенциалов на отдельных участках цепи и построение потенциальной диаграммы для исходной схемы.

Решение.

В схеме ключ S₁ разомкнут и ветвь с резистором R₆ не подключена к цепи.

Используя закон Ома для полной цепи (с учетом 2-го закон Кирхгофа) определим ток в цепи контура и его направление (не учитывая цепь с элементом R₆).

I = (E₁–E₂+E₃)/(R₁+R₂+R₃+R₄+R₅) = 0,5 (A).

Определим падения напряжений на отдельных элементах цепи.

Расчет начинают от точки с потенциалом, равным нулю, например, φ_А= 0.

Свойство 1. Если направление источника ЭДС совпадает с направлением обхода контура, то этому источнику в выражении присваивают знак плюс (+), а его вектор на потенциальной диаграмме направлен вертикально вверх, а если направление не совпадает, то вектор источника ЭДС направлен вертикально вниз.

Свойство 2. Если направление тока совпадает с направлением обхода контура, то этому току в выражении присваивается знак минус (–), а его вектор на потенциальной диаграмме направлен вниз.

φ_А–φ_В–IR₁= 0; φ_В = φ_А– IR₁; φ_B = 0–0,5∙4. φ_B = – 2 v.

φ_B–φ_C +E₁ = 0; φ_C = φ_B + E₁. φ_C = –2 + 7. φ_C = + 5 v.

φ_C–φ_D–I∙R₂=0; φ_D = φ_C – I∙R₂. φ_D = 5 –0,5∙6. φ_D = + 2 v.

φ_D–φ_E–I∙R₃ =0; φ_E = φ_D –I∙R₃. φ_E = 2 –0,5∙2. φ_E = + 1 v.

φ_E–φ_F – E₂ = 0; φ_F = φ_E – E₂. φ_F = 1 – 4. φ_F = – 3 v.

φ_F–φ_G–I∙R₄= 0; φ_G = φ_F –I∙R₄. φ_G = –3–0,5∙4. φ_G = – 5 v.

φ_G–φ_H+E₃ = 0; φ_H = φ_G + E₃. φ_H = – 5 + 9. φ_H = + 4 v.

φ_H–φ_A–I∙R₅=0; φ_A = φ_H – I∙R₄. φ_A = 4 –0,5∙8. φ_A = 0 v.

На потенциальной диаграмме по оси абсцисс откладывают суммарное сопротивление R цепи, а по оси ординат – падения напряжений и источники ЭДС.

Затем строят диаграмму, откладывая векторы потенциалов (падения напряжений на соответствующих элементах цепи).

Порядок выполнения лабораторной работы

1) Ознакомиться со схемой и устройством стенда (рис. 2.3) и записать технические характеристики используемых устройств и приборов.

2) Включить стенд и установить величины источников ЭДС, согласно задания.

3) Записать напряжения Е_ХХ.i источников ЭДС при отключенных нагрузках.

4) Измерить рабочие параметры цепи и данные измерений занести в табл. № 2.

5) Построить потенциальную диаграмму для выбранного обхода контура, для чего, условно заземлить схему в произвольно взятой точке.

Опыт №1. При включенном источнике ЭДС Е₁ и отключенном источнике ЭДС E₂ измерить падения напряжений U₁  U₃ и токи I₁  I₃ на элементах R₁  R₃.

Опыт №2. При включенном источнике ЭДС Е₂ и отключенном источнике ЭДС E₁ измерить падения напряжений U₁  U₃ и токи I₁  I₃ на элементах R₁  R₃.

Опыт №3. При включенных источниках ЭДС Е₁ и Е₂ измерить падения напряжений U₁U₃ и токи I₁  I₃ на элементах R₁R₃.

Определить направление токов для каждого опыта в исследуемой схеме.

Используя значения R₁R₃ и r_И.1, r_И.2 (из опыта №3) составить уравнения по законам Кирхгофа и определить теоретические значения токов: I₁ I₃.

* В данных опытах ветвь с резистором R₄ разомкнута (и не рассмотрена)!

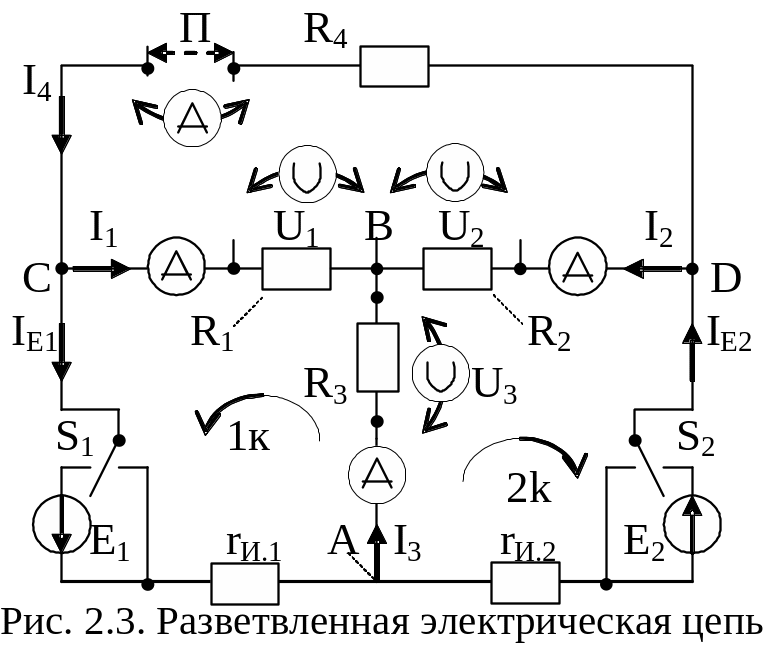В схеме стенда можно изменять по-лярность подключения источников ЭДС. Переключатели S₁ и S₂ в схеме служат для отключения/подключения источников ЭДС Е₁ и E₂. При отключении любого источника ЭДС, данная ветвь будет зашунтировать, т.е. при любом положении переключателей S₁ и S₂, контуры (1 и 2) замкнуты.

Перемычка П позволяет подключить к схеме ветвь с резистором R₄.

Таблица 2.1. Параметры измерений и вычислений для трех опытов

№

ЭДС

Измерено

Вычислено

№

Е1

Е2

U1

U2

U3

I1

I2

I3

R1

R2

R3

rИ.1

rИ.2

PИ

PН

PП

1

*

–

2

–

*

3

*

*

Токи теоретические IТЕОР:

*

*

*

Изм.

Изм.

Изм.

Вопросы для самоконтроля

1. Сформулируйте законы Ома, первый и второй закон Кирхгофа.

2. Понятие: узел, ветвь, контур, электрическая цепь, схема?

3. Дать понятие контурного сопротивления и контурного тока?

4. Как строят потенциальную диаграмму и что она отражает?

5. Условие передачи максимальной мощности от источника в нагрузку.

6. Условие баланса мощностей для цепи с несколькими источниками.

Литература

1. Касаткин А.С., Немцов М.В. Электротехника. – М.: Высш. шк., 2003. – 540 с.

2. Рекус Г.Г., Чесноков В.Н. Лабораторный практикум по электротехнике и основам электроники: Учебное пособие. – М.: Высш. шк., 2001. – 255 с.

3. Рекус Г.Г. Основы электротехники и промышленной электроники в примерах и задачах с решениями: Учебное пособие. – М.: Высш. шк., 2008. – 343 c.