2. Характеристики форми розподілу

Аналіз закономірностей розподілу передбачає оцінювання ступеня однорідності сукупності, асиметрії та ексцесу розподілу.

Однорідність сукупності – передумова використання інших статистичних методів (середніх величин, регресійного аналізу тощо). Однорідними вважаються такі сукупності, елементи яких мають спільні властивості і належать до одного типу, класу. При цьому однорідність означає не повну тотожність властивостей елементів, а лише наявність у них спільного в істотному, головному.

В однорідних сукупностях розподіли одновершинні (одномодальні). Багатовершинність свідчить про неоднорідний склад сукупності, про різнотиповість окремих складових. У такому разі необхідно перегрупувати дані, виокремити однорідні групи. Критерієм однорідності сукупності вважається квадратичний коефіцієнт варіації.

Асиметрія А_х характеризує ступінь несиметричності розподілу відносно його середнього. Позитивна асиметрія вказує на відхилення вершини розподілу в бік від'ємних значень, негативна – у бік додатних.

Коефіцієнт асиметрії вираховується за формулою:

Де z_x – міра Пірсона

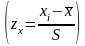
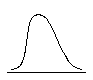
Негативна асиметрія, симетричний розподіл Позитивна асиметрія

А_s˂0 А_s=0 А_s˃0

Мал. 5.3. Типи асиметрій

Відповідність емпіричного розподілу нормальному знаходиться за відповідними таблицями. При цьому емпіричний розподіл вважається відповідним теоретичного (нормальному), якщо асиметрія при даній вибірці не перевищує граничного значення (As_эксп. < As_кр).

Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена ліворуч, маємо правосторонню асиметрію, і навпаки. Зазначимо, що асиметрія виникає внаслідок обмеженої варіації в одному напрямі або під впливом домінуючої причини розвитку, яка призводить до зміщення центра розподілу. Ступінь асиметрії різний – від помірного до значного. Рівновіддалені від центра значення ознаки мають однакові частоти.

Як уже зазначалося, у симетричному розподілі характеристики центра – середня, мода, медіана – мають однакові значення, в асиметричному між ними існують певні розбіжності.

Причини асиметрії можуть бути різними. По-перше, це можлива дія побічних односпрямованих факторів. Так, наприклад, в тестах на вимірювання інтелекту можуть переважати складні завдання, з якими більшість досліджуваних не справляється. Це може з'явитися причиною позитивної асиметрії (центральна тенденція лежить зліва від середнього значення). По-друге, це обмеження (зверху чи знизу) розмаху варіацій. Наприклад, при вимірюванні часу сенсомоторної реакції нижня межа реагування лімітований фізіологічними можливостями суб'єкта, в той час як верхній жорстко не обмежений. Нарешті, третьою причиною асиметрії може бути неоднорідність вибірки (наприклад, якщо дослідження проводиться в змішаній групі різного віку). При цьому має місце накладення один на одного двох або декількох різних за чисельністю і зсунутих відносно один одного по моді розподілів.

Іншою властивістю одновершинних розподілів є ступінь зосередженості елементів сукупності навколо центра розподілу. Цю властивість називають ексцесом розподілу. Ексцес E_x характеризує відносну опуклість або згладженість розподілу вибірки порівняно з нормальним розподілом. Позитивний ексцес позначає відносно загострений розподіл, негативний – відносно згладжений. Причинами ексцесу можуть бути більша або менша ступінь тяжіння змінних до центральної тенденції, неоднорідність вибірки, накладення один на одного декількох розподілів з однаковою модою та різною дисперсією і т. д. Вирахування показнику ексцесу за формулою:

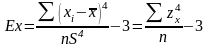
Плосковершинний Нормальний Гостровершинний

розподіл розподіл розподіл

Ex < 0 Ex = 0 Ex > 0